2.6. Передаточные функции замкнутой сау по задающему воздействию и возмущению

Большинство структурных схем САУ с помощью рассмотренных ранее преобразований можно привести к виду, приведенному на рисунке 2.52.

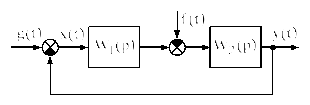
Рисунок 2.52

Введем обозначения:

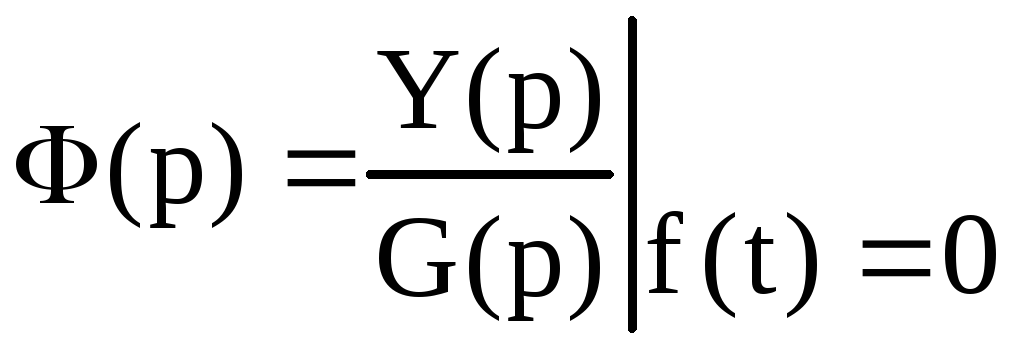(2.124) – передаточная функция замкнутой системы по зада­ю­щему воздействию.

Определяет связь между выходной величиной и задающим воздействиемпри возмущении;

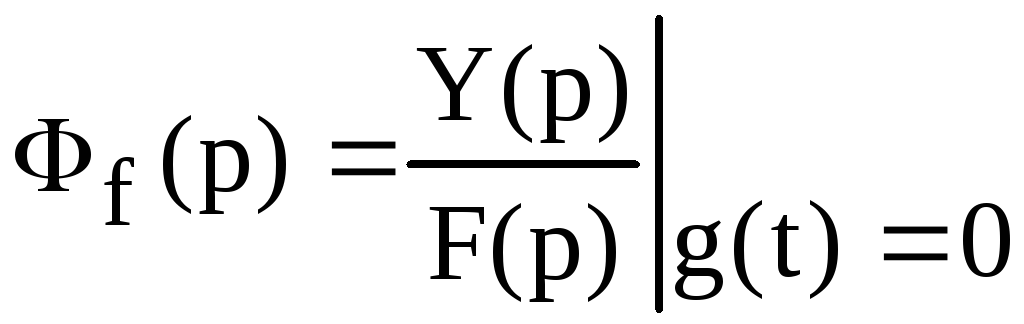–передаточная функция замкнутой системы (2.125) по возмущающему воздействию.

Определяет связь между выходной величиной и возмущениемпри задающем воздействии;

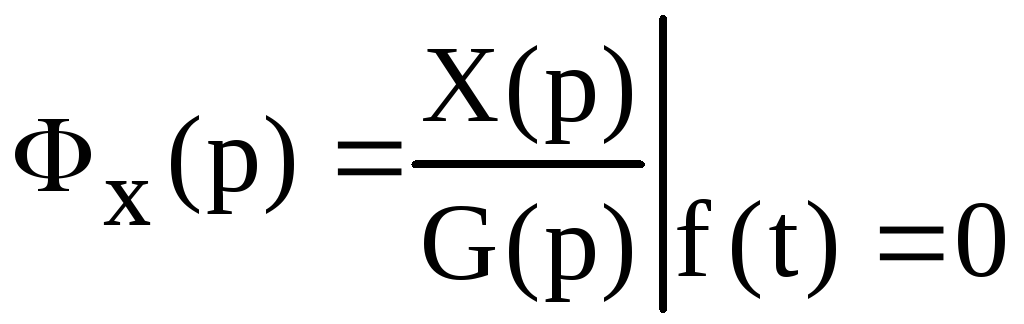–передаточная функция замкнутой системы (2.126) относительно ошибки по задающему воздействию.

Определяет связь между ошибкой регулирования и задающим воздействиемпри возмущении;

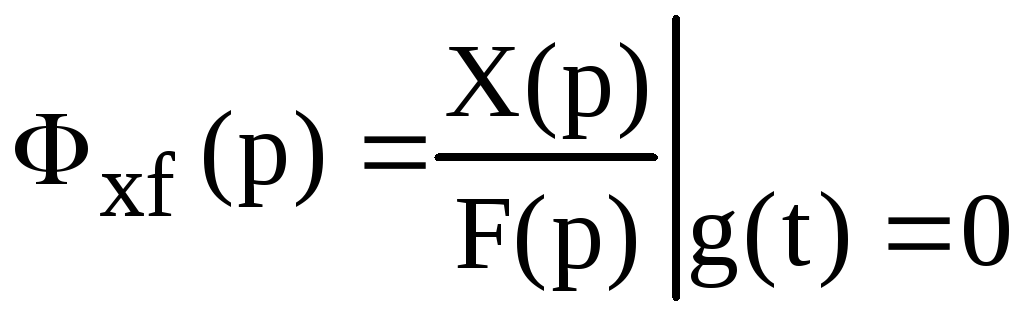–передаточная функция замкнутой системы относительно ошибки по возмущающему воздействию. (2.127)

Определяет связь между ошибкой регулирования и возмущениемпри задающем воздействии.

Сформируем передаточные функции (2.124) – (2.127) с помощью правила (2.122). Очевидно, что передаточная функция разомкнутой цепи будет одинаковой для всех формул (2.124) – (2.127):

. (2.128)

С этим результатом совпадает передаточная функция прямой цепи от точки приложения до выходной величины(составляющая формулы (2.124)):

. (2.129)

Тогда передаточная функция замкнутой системы по управляющему воздействию (2.124) принимает вид

. (2.130)

Передаточная функция прямой цепи от точки приложения возмущения до выходной величины(составляющая формулы (2.125)):

. (2.131)

В результате передаточная функция замкнутой системы по возмущающему воздействию (2.125) принимает вид

. (2.132)

Передаточная функция прямой цепи от точки приложения до ошибки регулирования(составляющая формулы (2.126)):

. (2.133)

Тогда передаточная функция замкнутой системы относительно ошибки по задающему воздействию (2.126) принимает вид

. (2.134)

Передаточная функция прямой цепи от точки приложения возмущения до ошибки регулирования(составляющая формулы (2.127)):

. (2.135)

В результате передаточная функция замкнутой системы относительно ошибки по возмущающему воздействию (2.127) принимает вид

. (2.136)

Полученные четыре передаточные функции (2.130), (2.132), (2.134), (2.136) содержат всю информацию о качестве функционирования системы, например, изображение управляемой координаты определяется как

, (2.137)

а ошибки регулирования

. (2.138)

Формулы (2.137) и (2.138) позволяют рассчитать переходные процессы в замкнутой САУ, определить время регулирования, перерегулирование и величину установившейся ошибки.

Запишем передаточную функцию прямой цепи (2.129) в виде

. (2.139)

Тогда передаточная функция замкнутой системы по управляющему воздействию (2.130)

, (2.140)

где –характеристический полином замкнутой САУ.

(2.141)

Передаточная функция замкнутой системы относительно ошибки по задающему воздействию (2.134) с учетом формулы (2.139) будет

. (2.142)