Принцип действия отража­тельной дифракционной ре­шетки.

Алюминированный слой обладает хорошей отража­тельной способностью как в видимой, так и в УФ и ИК об­ластях спектра. В отражатель­ной дифракционной решетке происходит дифракция и интер­ференция параллельных пуч­ков лучей от большого числа одинаковых штрихов. Для разложения света в спектр надо напра­вить свет параллельными пучками на дифракционную решетку (в спектральном приборе эту функцию выполняет объектив кол­лиматора), параллельные пучки от разных штрихов со­брать в точку в фокальной поверхности фокусирующего объектива (рис. 64).

Для простоты рассмотрим интерференцию двух лучей, идущих от соседних штрихов решетки (рис. 65). Поверхности решетки они достигают в разное время: луч II отстает от луча I, т. е. для этих лучей имеется разность хода Д. Проведем фронт вол­ны Л В. До него лучи доходят одновременно, следовательно, от­резок ВС — разность хода этих лучей. Из треугольника ABC находим

∆₁ = BC = d∙sini

Рис. 65. К выводу формулы отражательной дифракционной ре­шетки:

АВ — фронт волны падающих лучей I и II; ВС — разность хода лучей I и II; DC—фронт волны дифрагированного луча (лучи I’ и II’); AD— разность хода I’ и II’ лучей; i—угол падения; φ — угол дифракций лу­чей, дифрагированных от двух соседних штрихов

Отраженный от штрихов свет идет во всех направлениях. Рассмотрим одно из них — под углом φ (лучи I’ и II’). Разность хода лучей I’ и II’ DA равна ∆₂ = DA = d∙sinφ.

Фокусирующим объективом эти лучи собираются в точке М. Результат их

интерференции зависит от алгебраической суммы ВС и DC:

∆₂ – ∆₁ = d∙sinφ – d∙sini = d(sinφ – sini)

По условию максимума при интерференции следует

d(sinφ – sini) = kλ

Приведенное уравнение является формулой дифракционной решетки. В точке М (рис. 65) усиленными оказываются только те длины волн, для которых разность хода удовлетворяет условию максимума. Лучи, отраженные под другим углом, собираются в другой точке и усиливаются в ней лучи уже других длин волн, для которых удовлетворяется условие максимума. Чем больше угол φ, тем больше разность хода при данном i и тем большая длина вол­ны, удовлетворяя условию максимума, усиливается. Именно по­этому и происходит разложение света по длинам волн в дифрак­ционной решетке.

Спектры разных порядков.

По условию максимума усиление света при интерференции происходит всякий раз, когда разность хода равна целому числу длин волн. Поэтому одна и та же длина волны усиливается не в одном направлении, а во всех тех, для ко­торых разность хода кратна длине волны. Благодаря этому в отличие от призмы решетка дает не один спектр, а сразу множест­во. Число k в формуле решетки d(sinφ – sini) = kλ

определяет порядок спектра. При k = 0 получается спектр нулевого порядка, для ко­торого φ = i, т. е. sinφ – sini =0,

В этом случае независимо от длины волны разность хода рав­на нулю. Здесь фактически имеет место простое отражение света, не сопровождающееся разложением в спектр. Лучи всех длин волн усиливают друг друга. При k=l получается спектр первого поряд­ка, для которого разность хода равна одной длине волны. При раз­ности хода в две, три, четыре и т. д. длины волны (k = 2, 3, 4 ...) получаются соответственно спектры второго, третьего, четвертого и т. д. порядков (рис. 66) .

Таким образом, часть излучения, падающего на решетку, отра­жается от нее, как от обычного зеркала, не разлагаясь в спектр, а другая часть распределяется между спектрами разных порядков. Если бы штрихи решетки были плоскими, то наибольшая доля энергии падающего на решетку света пришлась бы в спектр нуле-

Рис. 66. Схематическое изображение распределения видимых спектров

различных порядков (кр — красная область; ф — фиолетовая)

Рис. 67. Решетка с профилированным штри­хом:

а —ширина штриха; d — постоянная решетки; β — угол блеска

вого порядка, т. е. большая часть света оказалась бы неразложенной по длинам волн. Спектры первого, второго, третьего и т. д. порядков оказались бы малой интенсивности, причем с увеличени­ем порядка интенсив­ность спектра уменьша­лась бы пропорционально квадрату порядка. По­этому в настоящее время изготовляют отражатель­ные дифракционные ре­шетки с профилирован­ными штрихами (рис. 67). Решетки с такими штри­хами концентрируют энер­гию излучения в спектрах

более высоких порядков (рис. 68). Порядок наиболее интенсивного спектра определяется глубиной штриха и углом блеска β (см. рис. 67). Углом блеска называют угол между перпендикуляром к поверхности решетки и перпендикуляром к отражающей грани штриха. Решетка концентрирует энергию в направлении угла β.

Рис. 68. Распределение интенсивности по

порядкам спектров: а — для решетки с плоским штрихом; б — для решетки с профилированным штрихом (мак­симальная интенсивность в спектре 3-го по­рядка)

Решетки, имеющие сравнительно небольшой угол блеска и по­этому применяемые для работы в спектрах небольших порядков (2—10), называют эшелеттами. Решетки, предназначенные для ра­боты в высоких порядках (50 и более), имеют более глубокие штрихи с большим углом блеска. Их называют эшелле.

Спектры разных порядков могут частично перекрываться. На­пример, в одном и том же направлении лучей (одинаковый угол φ) разность хода равна одной длине волны — 700 нм (1-й порядок), двум длинам волн по 350 нм (2-й порядок), четырем длинам волн по 175 нм (4-й порядок) и т. д.

Степень перекрывания порядков характеризуется областью свободной дисперсии ∆λ. Величина ∆λ, представляет собой участок спектра, в пределах которого спектр данного порядка не перекры­вается спектром соседнего порядка. При увеличении порядка спек­тра область свободной дисперсии уменьшается: ∆λ =λ/k. Напри­мер, в спектре второго порядка для λ = 500 нм ∆λ составляет 250 нм, т. е. в пределах 250 нм (в длинноволновую и коротковол­новую области спектра) можно не опасаться появле­ния линий других порядков. В спектре сотого порядка для той же линии λ = 500 нм, а ∆λ — всего 5 нм.

Линии мешающих по­рядков удается устранить из спектра при помощи опти­ческих или интерференцион­ных фильтров, подбором со­ответствующей регистрирую­щей системы, нечувстви­тельной к мешающей обла­сти спектра, или с помощью монохроматора небольшой дисперсии.

Угловая дисперсия ре­шетки тем больше, чем боль­ше порядок спектра и мень­ше постоянная решетки: 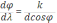, где

При сравнительно небольших углах дифракции угловая диспер­сия решетки в пределах одного порядка постоянна и не зависит от длины волны:

где N — общее число штрихов. Этим решетка выгодно отличается от призмы, у которой угловая диспер­сия изменяется с изменением длины волны.

Из последнего выражения видно, что угловая дисперсия возрас­тает с увеличением порядка спектра. Поэтому, наиболее целесооб­разно использовать в спектральных приборах решетки с профили­рованным штрихом с большим углом блеска. При этом одновре­менно достигается и большая угловая дисперсия и высокая интен­сивность спектра. Необходимо только позаботиться об устранении перекрывания порядков.