Множественная регрессионная модель

Классическая линейная модель множественной регрессии

Экономические явления, как правило, определяются большим числом одновременно и совокупно действующих факторов. В связи с этим часто возникает задача исследования зависимости одной зависимой переменной у от нескольких объясняющих переменных. Эта задача решается с помощью множественного регрессионного анализа.

Модель множественной линейной регрессии можно представить в виде:

y_i = β₀+ β₁x_i1 +β₂x_i2+ … +β_px_ip + ɛ_i (1)

где y_i – значения результирующей переменной; x_i1 , x_i2 ,… , x_ip – значения 1-го, 2-го, …, р-го регрессора в i-том наблюдении (i=1,2, … , n); β₀, β₁, β₂, …, β_p – числовые коэффициенты; ɛ_i – случайные (стохастические) составляющие или ошибки (возмущения), удовлетворяющие необходимым предпосылкам […].

Оценкой модели (1) по выборке при i=1,2, … , n является уравнение

ŷ_i=а₀+а₁x_i1 + а₂x_i2 + … + а_рx_ip

где ŷ_i - аппроксимирующие значения зависимой переменной; а₀,а₁,а₂, … , а_р - выборочные оценки соответствующих коэффициентов. Они находятся также с помощью метода МНК.

Коэффициент регрессии 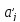показывает, на сколько изменится в среднем зависимая переменная у при увеличении только j-той объясняющей переменной на единицу собственного измерения.

Множественный коэффициент детерминации (R²) характеризует, какая доля вариации результативного признака обусловлена изменением факторных признаков, входящих в многофакторную регрессионную модель.

Частный коэффициент детерминации показывает, на сколько процентов вариация результативного признака объясняется вариацией j-того признака, входящего в регрессионную модель.

На практике часто бывает необходимо сравнение влияния на зависимую переменную различных объясняющих переменных, когда последние выражаются разными единицами измерения. В этом случае используют стандартизированные коэффициенты регрессии:

= а_j

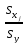
Стандартизованный коэффициент регрессии 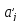показывает, на сколько величин s_y изменится в среднем зависимая переменная у при увеличении только j-той объясняющей переменной на .

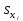Оценка значимости коэффициентов регрессии β₀, β₁, β₂, …, β_p проводится аналогично как и для парной линейной регрессии. Но t_кр = t_кр (α; к=n-р-2).

Для оценки значимости уравнения регрессии естественно использовать аналогичную величину

F=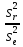= (n-р-1),

ибо в уравнении множественной регрессии вместе со свободным членом оценивается m=p+1 параметров.

Следовательно, нулевая гипотеза о не значимости уравнения регрессии в целом (об одновременном равенстве нулю всех коэффициентов при факторных переменных) составляет Н₀: β₁= β₂=…= β_p=0. Альтернативная гипотеза H₁ : хотя бы одно β_j≠0, j=1,2, … , p.

Критическая точка F_кр= F_кр (α; к₁=р, к₂=n-р-1).

Если известен коэффициент детерминации R² , то критерий значимости уравнения регрессии может быть записан в виде:

F=

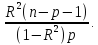
В случае парной регрессии проверка нулевой гипотезы для t-статистики коэффициента регрессии равносильна проверке нулевой гипотезы для F- статистики. Самостоятельную значимость R² имеет для множественной регрессии. Он используется для анализа общего качества оцененной линейной регрессии (в случае парной регрессии это квадрат коэффициента корреляции переменных х и у).

Множественный коэффициент детерминации может быть вычислен по формуле:

Он характеризует долю вариации (разброса) зависимой переменной, объясненной с помощью данного уравнения (см. рис. ….).

Из рис. видно, что с добавлением еще одной переменной R² обычно увеличивается. Однако если объясняющие переменные х₁ и х₂ сильно коррелируют между собой, то они объясняют одну и ту же часть разброса переменной у, и в этом случае трудно идентифицировать вклад каждой переменной в объяснение поведения у.

Для определения статистической значимости коэффициента детерминации R² проверяется нулевая гипотеза F-статистики (см….).

Проблема размерности регрессионной модели

Следует отметить, что включенные в регрессионную модель объясняющие переменные не должны противоречить теоретическим положениям соответствующей предметной области моделируемого явления. Меняя состав переменных, получаются новые уравнения регрессии. При этом в пользу добавления в модель (исключения из модели) каждой переменной могут свидетельствовать: значимость (незначимость коэффициента регрессии), возрастание скорректированного? коэффициента детерминации, значительное (незначительное) изменение других коэффициентов регрессии.

Наиболее приемлемым способом отбора факторных признаков является пошаговая регрессия. Сущность этого метода заключается в последовательном включении факторов в уравнение регрессии и последующей проверке их значимости. При проверке значимости введенного фактора определяется, насколько уменьшается сумма квадратов остатков и увеличивается величина множественного коэффициента корреляции. Одновременно можно исключать факторы, ставшие незначимыми на основе t-критерия Стьюдента. Фактор является незначимым, если его включение в уравнение регрессии только изменяет значение коэффициентов регрессии, не уменьшая суммы квадратов остатков и не увеличивая их значения. Если при включении в модель соответствующего факторного признака величина множественного коэффициента корреляции увеличивается, а коэффициент регрессии не изменяется (или меняется несущественно), то данный признак существенный.

Если же при включении в модель факторного признака коэффициенты регрессии меняют не только величину, но и знаки, а множественный коэффициент корреляции не возрастает, то данный признак нецелесообразно включать в модель.

Проблема размерности регрессионной модели, т.е. определение оптимального числа факторных признаков, является одной из основных проблем построения множественного уравнения регрессии. С одной стороны, чем больше факторных признаков включено в уравнение, тем оно лучше описывает явление. Однако при большом их количестве регрессионная сложна в реализации. Сокращение размерности модели может привести к тому, она будет недостаточно адекватна исследуемым процессам и явлениям.

Пусть рассматриваются два уравнения регрессии:

у=a₀ + а₁х₁ (1)

у= a₀ + а₁х₁ + а₂х₂ (2)

Во втором уравнении коэффициент а₁ регрессии позволяет оценить прирост зависимой переменной у при изменении на единицу объясняющей переменной х₁ в чистом виде, независимо от х₂. В случае парной регрессии а₁ учитывает воздействие на у не только переменной х₁, но и косвенно связанной с ней переменной от х₂.

Адекватность уравнения регрессии [Шмойлова]

При анализе адекватности уравнения регрессии исследуемому процессу возможны следующие варианты:

1. Построенная модель на основе ее проверки по F-критерию Фишера в целом адекватна, и все коэффициенты регрессии значимы. Такая модель может быть использована для принятия решений и осуществления прогнозов.

2. Модель по F-критерию Фишера адекватна, но часть коэффициентов регрессии незначима. В этом случае модель пригодна для принятия некоторых решения, но не для прогнозов.

3. Модель по F-критерию Фишера адекватна, но все коэффициенты регрессии незначимы. В этом случае модель полностью считается неадекватной. На ее основе не принимаются решения, и не осуществляются прогнозы.