
Статистические свойства оценок коэффициентов регрессии:
- оценки коэффициентов a0 , a1 являются несмещенными;
- дисперсии оценок a0 , a1 уменьшаются (точность оценок увеличивается) при увеличении объема выборки n;
-
дисперсия оценки углового коэффициента
a1
уменьшается
при увеличении
 и
поэтому желательно выбирать хi
так,
чтобы их разброс вокруг среднего значения
и
поэтому желательно выбирать хi
так,
чтобы их разброс вокруг среднего значения
 был большим;
был большим;
- при х¯ > 0 (что представляет наибольший интерес) между a0 и a1 имеется отрицательная статистическая связь (увеличение a1 приводит к уменьшению a0).
Теорема Гаусса – Маркова
Если регрессионная модель (1) удовлетворяет условиям 1)-4), МНК оценки a0 и a1 , полученные из системы 4), имеют наименьшую дисперсию в классе всех линейных несмещенных оценок (являются наиболее эффективными).
Оценка значимости и доверительных интервалов для коэффициентов регрессии
Пусть β0j - заданное гипотетическое значение j-го коэффициента регрессии (j=0,1). При оценке значимости коэффициентов регрессии β1 и β0 формулируются следующие гипотезы:
H0 : βj = β0j
H1: β ≠ β0j
Статистикой критерия является случайная величина
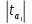 =
(
aj
-
=
(
aj
-
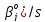 aj
(5)
aj
(5)
При условии выполнения нулевой гипотезы Ho имеющая распределение Стьюдента с к=n-2 степенями свободы. Критическая область, как следует из вида конкурирующей гипотезы H1, является двусторонней.
Критическая точка tкр = tкр (α; к=n-2) находится по статистическим таблицам или с помощью стандартных функций в пакетах прикладных программ.
Наиболее просто статистика (4) выглядит при β0j=0, когда
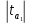 =
=
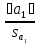
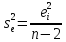
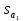 =
=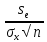 =
=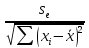
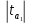 =
=

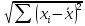 (6)
(6)
В этом случае при оценке значимости коэффициентов регрессии β1 и β0 гипотезы имеют следующий вид:
H0 : βj = 0
H1: β ≠ 0
Нулевая гипотеза принимается в случае, когда ׀taj׀ ≤ tкр и с уровнем значимости α делается вывод о том, что коэффициент βj незначим. Альтернативная гипотеза принимается в случае, когда ׀taj׀ > tкр tкр и с уровнем значимости α делается вывод о том, что коэффициент βj значим (имеется статистическая связи между х и у).
Именно такой подход используется в компьютерных пакетах. При использовании этого подхода обычно дополнительно вычисляется так называемое p-значение.
Анализ вариации зависимой переменной (дисперсионный анализ)
Согласно
идее дисперсионного анализа, общую
сумму квадратов (вариацию или разброс
yi
вокруг среднего значения
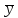 )
)
Q=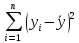
можно разбить на две части – объясненную уравнением регрессии и необъясненную (остаточную):
Q=Qr +Qe ,
где
Qr=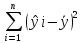 – сумма квадратов, объясненная регрессией;
– сумма квадратов, объясненная регрессией;
Qe=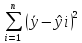 – остаточная сумма квадратов,
характеризующая влияние случайных
(неучтенных) факторов.
– остаточная сумма квадратов,
характеризующая влияние случайных
(неучтенных) факторов.
Выборочный коэффициент детерминации
Выборочный коэффициент детерминации показывает, какая доля вариации зависимой переменной обусловлена вариацией объясняющей переменной и определяется выражением
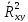 =
=
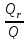 = 1 -
= 1 -
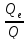
Свойства
коэффициента
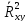 :
:
Коэффициент
 служит для оценки значимости уравнения
регрессии, в том числе линейной и
множественной.
служит для оценки значимости уравнения
регрессии, в том числе линейной и
множественной.Коэффициент
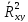 – состоятельная оценка генерального
коэффициента детерминации
– состоятельная оценка генерального
коэффициента детерминации
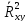 (при выполнении 5-го условия КЛМПР).
(при выполнении 5-го условия КЛМПР).Коэффициент
 – безразмерная величина, лежащая в
пределах
– безразмерная величина, лежащая в
пределах
0
≤
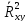 ≤
1.
≤
1.
При
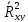 =0
вариация зависимой переменной полностью
обусловлена воздействием неучтенных
в модели переменных (случайных факторов)
и линия регрессии параллельна оси
абсцисс (Qr=0,
Q=Qe).
=0
вариация зависимой переменной полностью
обусловлена воздействием неучтенных
в модели переменных (случайных факторов)
и линия регрессии параллельна оси
абсцисс (Qr=0,
Q=Qe).При
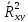 =1
все эмпирические точкиyi
лежат на линии регрессии, и между х и
у имеется линейная функциональная
завиисмость (Qr
=Q,
Qe=0).
=1
все эмпирические точкиyi
лежат на линии регрессии, и между х и
у имеется линейная функциональная
завиисмость (Qr
=Q,
Qe=0).Для линейной парной регрессии (в общем случае это неверно)
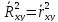 .
В общем случае коэффициент
.
В общем случае коэффициент =
= иногда называют множественным
коэффициентом корреляции.
иногда называют множественным
коэффициентом корреляции.
Оценка значимости уравнения регрессии
Проверить значимость уравнения регрессии – значит установить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных (одной или нескольких) для описания зависимой переменной.
Проверка значимости уравнения регрессии проводится на основе регрессионного анализа. Для оценки значимости уравнения регрессии естественно использовать величину
F=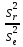 =
=
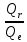 (n-2),
(*)
(n-2),
(*)
которая
показывает, во сколько раз объясненная
(факторная) дисперсия превышает
остаточную. Понятно, что при отсутствии
какой-либо линейной статистической
связи между зависимой и предикторной
переменной (при β=0 и, следовательно,
незначимости уравнения регрессии)
факторная
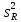 и остаточная
и остаточная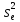 дисперсии будут близкими друг к другу,
и величинаF
будет мала. В этом случае статистика
(*) имеет распределение Фишера-Снедекора
(F
– распределение) с к1=1
и к2=n-2
степенями свободы числителя и знаменателя.
дисперсии будут близкими друг к другу,
и величинаF
будет мала. В этом случае статистика
(*) имеет распределение Фишера-Снедекора
(F
– распределение) с к1=1
и к2=n-2
степенями свободы числителя и знаменателя.
Следовательно, нулевая гипотеза о незначимости уравнения регрессии Н0: β1=0.
Критическая точка Fкр= Fкр (α; к1=1, к2=n-2) находится по таблицам критических точек или с помощью стандартных функций в пакетах компьютерных программ.
Нулевая гипотеза принимается, когда F< Fкр и с уровнем значимости α делается вывод о том, что уравнение регрессии значимо.
В противном случае, когда F≥ Fкр с уровнем значимости α делается вывод о том, что уравнение регрессии значимо.
Величину F можно выразить в эквивалентном виде
F=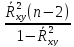 ,
(**)
,
(**)
из
которого вытекает явный экономический
смысл – чем ближе коэффициент
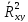 к 1, тем более значимо уравнение регрессии
(хорошая аппроксимация эмпирических
данных).
к 1, тем более значимо уравнение регрессии
(хорошая аппроксимация эмпирических
данных).
Легко показать (см. Приходько с.17,20), что выполняется соотношение
F= =
=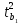 ,
справедливое, однако только для случая
парной регрессии, когда корень из
статистики (**):
,
справедливое, однако только для случая
парной регрессии, когда корень из
статистики (**):
tr=
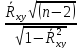 =
=
 ,
,
имеет распределение Стьюдента с к=n-2 степенями свободы.
Доверительный интервал для значений зависимой переменной
Ошибка регрессионного предсказания равна разности между действительными yi и предсказанными ŷi значениями зависимой переменной
ei = yi - ŷi (***)
(ошибка (***) имеет нулевое математическое ожидание М[ei]=0). Соответствующий доверительный интервал для yi определяется по формуле
yi min < yi < yi max ,
где
yi
min
=
ŷi
–
tкр
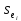 ,
yi
max
=
ŷi
+ tкр
,
yi
max
=
ŷi
+ tкр
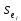 ,
tкр
=
tкр
(α;
к = n–2)
–
критическая точка распределения
Стьюдента с к = n–2
степенями свободы для уровня значимости
α.
,
tкр
=
tкр
(α;
к = n–2)
–
критическая точка распределения
Стьюдента с к = n–2
степенями свободы для уровня значимости
α.
Как
следует из (***) по мере удаления аргумента
xi
от среднего значения
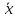 , ширина доверительного интервала
увеличивается.
, ширина доверительного интервала
увеличивается.
Пример 2. (парной линейной регрессии пример Кремер с.449).
