Desktop_1 / Лекции 1 симестр / механика2

Лекция №2

Механика

Кинематика поступательного и вращательного движения

(Материальная точка, система отсчета, перемещение, скорость, ускорение, основная задача кинематики)

Кинематика - это раздел механики, где изучаются способы описания движений независимо от причин, обусловливающих эти движения, то есть, в основном, геометрические свойства движения. Массы тел и действующие на них силы в кинематике не рассматриваются. В лекциях по кинематике рассмотрены три вопроса, необходимых для понимания физических основ механики: кинематика частицы, кинематика твердого тела и преобразование скорости и ускорения при переходе от одной системы отсчета к другой

     Если размеры тела при описании его движения несущественны, то его движение можно рассматривать как движение материальной точки в пространстве. Это самая простая модель для описания реального тела. Так как в дальнейшем будут рассматриваться движения тела обладающего массой, но в пренебрежении ее размерами, внутренней структуры и формы, то введем в рассмотрение единый термин частица, понимая под ним материальную точку. Существует несколько способов описания движения частицы: векторный (геометрический) и координатный. Рассмотрим их последовательно.

     Векторный способ. В этом способе положение интересующей нас частицы А задают радиусом-вектором , проведенным из некоторой неподвижной точки О выбранной системы отсчета в точку А. Под системой отсчета в механике понимают совокупность: тело отсчета, способ измерения расстояний ("линейка") и способ измерения времени ("часы"). При движении частицы А ее радиус-вектор меняется в общем случае как по модулю, так и по направлению, т. е. радиус-вектор зависит от времени t.

Рис. 2.1. Векторный способ описания движения частицы

     Геометрическое место точек, где тело побывало за время своего движения, называется траекторией частицы А. При векторном способе описания траекторией будет положение концов радиус-вектора во все моменты времени.

     Введем понятие скорости частицы. Скорость характеризует быстроту движения частицы. Пусть за промежуток времени точка А переместилась из точки 1 в точку 2 (рис. 2.1). Из рисунка видно, что вектор перемещения частицы А представляет собой приращение радиус-вектора за время (t : . Отношение называют средним вектором скорости <> за время (t. Вектор <> совпадает по направлению с . Определим теперь вектор скорости частицы в данный момент времени как предел отношения при t→ 0, т. е.

     

(2.1)

     Это значит, что вектор скорости частицы в данный момент времени равен производной от радиус-вектора по времени и направлен по касательной к траектории в данной точке в сторону движения частицы А (как и вектор ). Модуль вектора равен

     

     Заметим, что в общем случае модуль приращения радиус-вектора не равен изменению модуля радиус-вектора . Например, если меняется только по направлению при движении частицы по окружности, то но .

     Движение частицы характеризуется также ускорением. Вектор ускорения определяет скорость изменения вектора скорости со временем:

     

,

(2.2)

     т. е. равен производной от вектора скорости по времени. Направление вектора совпадает с направлением вектора - приращением вектора за время dt. Модуль вектора определяется аналогично модулю вектора . Пусть, например, радиус-вектор частицы зависит от времени t по закону

     

,

     где и - постоянные векторы. Найдем скорость и ускорение частицы: Модуль вектора скорости

     

.

     Таким образом, зная зависимость , можно найти скорость и ускорение частицы в каждый момент времени.

     Возникает и обратная задача: можно ли найти и , зная зависимость от времени ускорения ?

     Оказывается, для получения однозначного решения этой задачи одной зависимости недостаточно, так как необходимо еще знать начальные условия, а именно - скорость и радиус-вектор частицы в некоторый начальный момент . Чтобы в этом убедиться, рассмотрим простой случай, когда при движении ускорение частицы остается постоянным.

     Определим сначала скорость частицы . Согласно (2.2), за интервал времени dt малое приращение скорости . Интегрируя это выражение по времени от t = 0 до t, определим конечное приращение вектора скорости за это время:

     

.

     Но величина - это еще не искомая скорость . Для нахождения , необходимо знать скорость в начальный момент времени . Тогда , или

     

     Аналогично вычисляется и радиус-вектор частицы. Согласно (2.1), за интервал времени dt малое приращение радиус-вектора . После интегрирования этого выражения с учетом определенной выше зависимости , определим приращение радиуса-вектора за время от t = 0 до t:

     

.

     Для нахождения самого радиус-вектора необходимо знать положение частицы в начальный момент времени . Тогда ,

     или

     

.

     Координатный способ. В этом способе с телом отсчета жестко связывают определенную систему координат (декартову, косоугольную или криволинейную). Выбор вида системы координат определяется рядом соображений: характером или симметрией задачи, постановкой вопроса, а также стремлением упростить математическое решение задачи. Для простоты рассмотрим декартову систему координат x,у,z. Изучение движений частицы в других координатах оставим для задач.

     Запишем проекции радиус-вектора на оси координат. Вектор определяет положение интересующей нас частицы относительно начала координат О в момент t:

     

     Закон движения частицы - это зависимость координат от времени. Он задает положение частицы в каждый момент времени, ее скорость и ускорение. Cпроектировав (2.1) и (2.2), например, на OX, получим формулы, определяющие проекции векторов скорости и ускорения на эту ось:

     

,

(2.3)

      где dx- проекция вектора перемещения на ось х,

     

(2.4)

     здесь - проекция вектора приращения скорости на ось х. Такие же соотношения получаются для у- и z-проекций соответствующих векторов. Из этих формул видно, что проекции векторов скорости и ускорения равны соответственно первой и второй производным координат по времени.

     Зависимости полностью определяют движение частицы. Зная их, можно найти не только положение частицы, но и проекции ее скорости и ускорения, а следовательно, модуль и направление векторов и в любой момент времени. Например, модуль вектора скорости определяется формулой

     

,

     а направление вектора задается направляющими косинyсами по формулам:

     

(2.5)

     где , β ,γ - углы между вектором и осями х, у, z соответственно. Направляющие косинусы всегда удовлетворяют соотношению . Аналогичными формулами определяются модуль и направление вектора ускорения .

     С помощью закона движения можно найти траекторию частицы, зависимость пройденного ею пути от времени, зависимость скорости от положения частицы и т.д.

     Нахождение скорости и закона движения частицы по заданному ускорению называется обратной задачей. Ее решение проводится, как и в векторном способе, путем интегрирования (в данном случае проекций ускорения по времени). Задача и здесь имеет однозначное решение, если кроме ускорения заданы еще и начальные условия: проекции скорости и координаты частицы в начальный момент времени.

Вернемся к определению ускорения частицы . Выразим

   

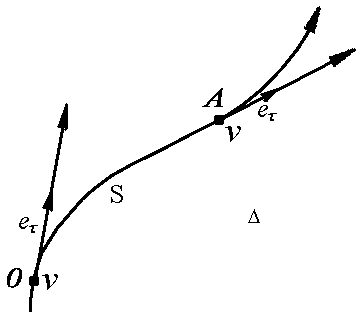
Здесь е_τ является еденичным вектором (ортом) вдоль направления вектора скорости. Отсюда:

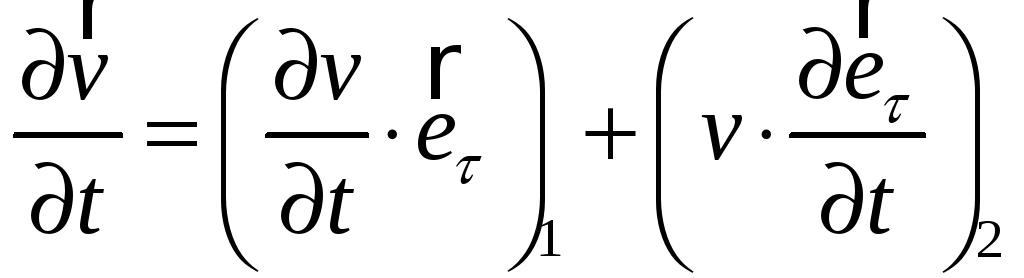
Первая часть нашего равенства характеризует изменение модуля скорости со временем и направлена вдоль вектора скорости эта часть носит название: линейное или тангенциальное ускорение.

Перейдем ко второй части равенства. Рассмотрим изменение единичного вектора е_τ при его повороте за малый промежуток времени t . Для этого совместим начало вектора е_τ в первоначальный момент времени с началом этого вектора в момент времени через промежуток t . При этом вектор соединяющий конец первого вектора с концом второго вектора будет приращением (разностью) этих векторов е_τ .

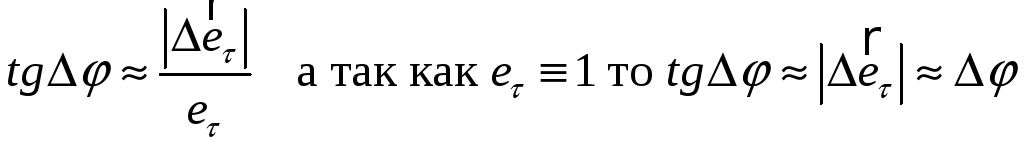
При малом повороте вектора е_τ

При малых 

Отсюда вторая исходное уравнение приобретает вид

Производная по времени от угла поворота есть угловая скорость. Представим угловую скорость в виде:

 

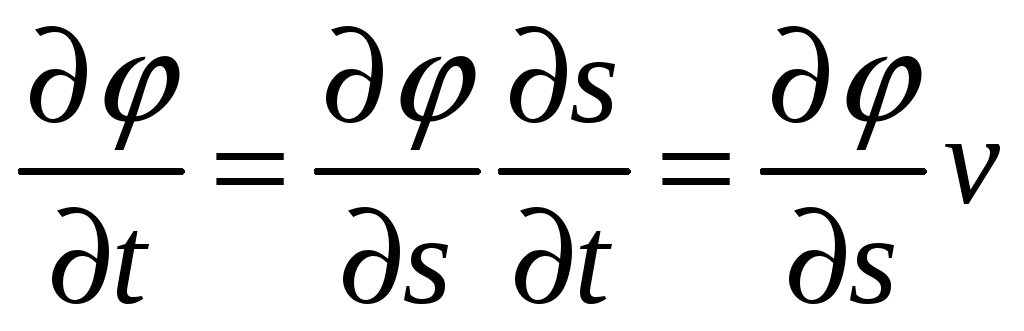
Таким образом, мы установили связь между абсолютными значениями угловой и линейной скоростью.

Исходное выражение для ускорения точки может быть записано в окончательном виде:

В этом выражении первый член правой части является тангенциальным ускорением, которое направлено в сторону или навстречу движению точки. Второй член называется нормальным или центростремительным ускорением. Центростремительное ускорение всегда перпендикулярно вектору скорости движения точки и направлено к центру кривизны траектории.

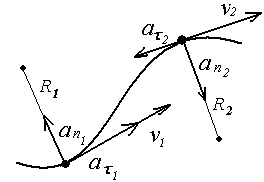
Полное ускорение направлено находится по правилу векторного сложения и является результирующим вектором векторов тангенциального и нормального ускорения. Его абсолютная величина определяется как:

Вернемся к рассмотрению вращательного движения, характеристиками которого является угол поворота тела и угловая скорость.

Угловая скорость, как и угол поворота, являются векторами (псевдо векторами) направление которых перпендикулярно плоскости вращения и совпадает с направлением вкручивания правого винта, если тот вращается в сторону рассматриваемого вращения.

Есть еще одна векторная характеристика вращательного движения, это угловое ускорение.

Направление этого вектора (псевдо вектора) совпадает или противоположно вектору угловой скорости в зависимости от того увеличивается или уменьшается угловая скорость объекта.

Равномерное вращение так же характеризуется периодом T (временем одного оборота тела) и частотой вращения  (количеством полных оборотов в единицу времени).

Период измеряется в секундах, частота - в обратных секундах, угол поворота - в радианах, угловая скорость - в радианах в секунду, угловое ускорение - в радианах в секунду за секунду.

Вернемся к выражению для углового ускорения, распишем его и получим связь между линейным и угловым ускорением

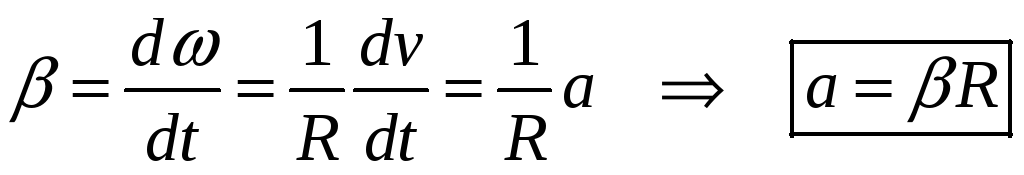
Основной задачей кинематики является нахождение положения движущейся матеоиальной точки, ее скорости, ускорения в любой интересующий нас момент времени.

Пусть известен вид функции, выражающей зависимость координат точки от времени

x = f₁(t), y =f₂(t), z = f₃(t). Тогда подставляя значение времени в эти выражения, получим координаты точкив интересующий момент времени. Продифференцировав по времени и продифференцировав дважды по времени функции определяющие координаты точки, получим соответственно значение компонент скорости и ускорения точки.

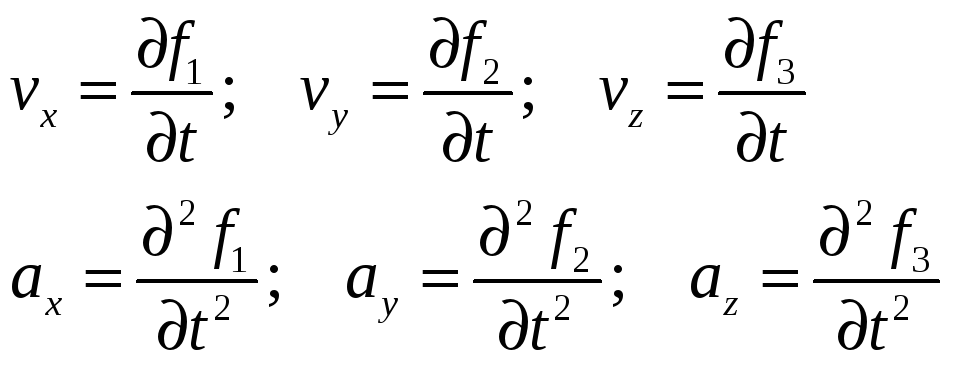
Возможно так же и обратная задача: по функциям выражающим временную зависимость компонент ускорения от времени найти компоненты скорости и координаты точки в интересующий момент времени. Эта задача решается совершением обратной операции интегрированием. Однократное интегрирование дает значение компонент скорости, двукратное дает значение координат точки.

Так как интегрирование определяет функцию с точностью до произвольной постоянной величины. Для решения поставленной задачи должны быть заданы начальные условия определяемые из дополнительных соображений.

Начальные условия это параметры механического состояния заданные в определенный момент времени. Обычно удобен для этих случаев начальный момент, когда t = 0 .