Desktop_1 / Лекции 1 симестр / механика10

ЛЕКЦИЯ №10

Представление колебаний с помощью векторной диаграммы. Сложение однонаправленных колебаний. Биения. Сложение колебаний колеблющихся в ортогональных плоскостях.

Особым случаем является процесс, при котором происходит сложение колебаний, при этом результирующим явлением будет тоже колебательный, но более сложный процесс. Рассмотрим случай сложения двух колебаний.

Колебания, из которых будет складываться результирующий процесс, могут быть однонаправленными и ортогональными (взаимно перпендикулярными). Нахождение результирующего колебания по известным параметрам исходных колебаний происходит по определенным правилам. Познакомимся с ними и начнем с однонаправленных колебаний.

Гармонические колебания могут быть представлены графическим способом на векторной диаграмме. Обозначим точку 0 через нее проведем ось х . Из точки 0 под некоторым углом  к оси х проведем вектор длиной а. Пусть вектор а вращается вокруг точки 0 с угловой скоростью ₀ . В этом случае величина проекции х вектора а на ось х может быть выражена уравнением:

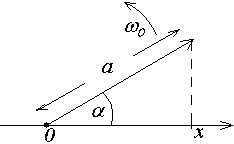
Следовательно, проекция конца вектора а будет совершать гармонические колебания с амплитудой а равной длине вектора, с начальной фазой равной начальному углу  между вектором и осью х и частотой колебаний равной угловой скорости ₀ вращения вектора.

Рассмотрим сложение двух гармонических однонаправленных колебаний.

Изобразим эти гармонические колебания на векторной диаграмме:

Частота вращения векторов а₁ и а₂ одинакова и равна₀ поэтому такой же будет частота вращения результирующего вектора. Вектора подчиняются правилу векторного сложения, поэтому результирующий вектор а будет равен векторной сумме исходных векторов а₁ и а₂ . Его величина будет равна диагонали параллелограмма стороны которого составляют исходные вектора.

Таким образом, величина результирующего вектора (амплитуда результирующего колебания):

При этом начальная фаза колебания находится из выражения:

Таким образом, результирующее колебание описывается выражением

Где амплитуда частота и начальная фаза колебания определяется выражениями описанными выше.

Если частота колебаний двух процессов неодинакова в результате получаются сложные негармонические колебания.

Особым является случай, когда складываются два однонаправленных гармонических колебания со слабо различающейся частотой.

Представим частоты двух колебаний, как  и  + , где  <<  . Для простоты будем полагать амплитуды колебаний одинаковыми и равными а , а так же положим, что начальная фаза обоих колебаний равна нулю.

В том случае рассматриваемые колебания можно описать выражениями:

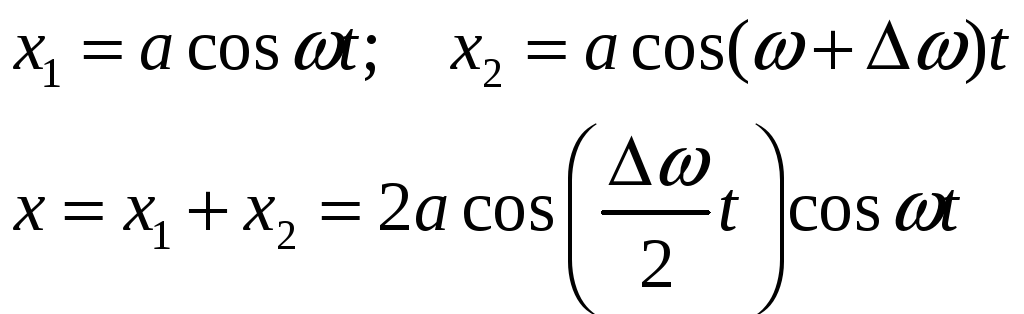
Во втором сомножителе мы пренебрегли малой величиной /2 в сравнении с  .

Таким образом, результирующие колебания могут быть представлены как гармонические колебания с частотой  и амплитудой зависящей от времени по периодическому закону и равной половине разности частот складываемых колебаний.

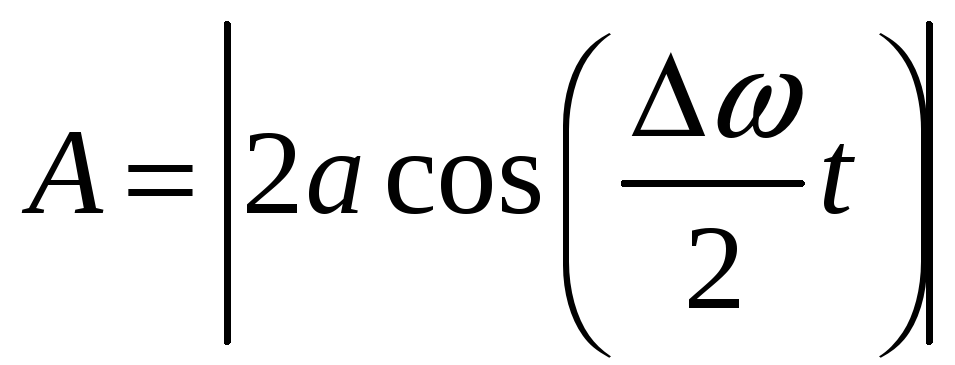
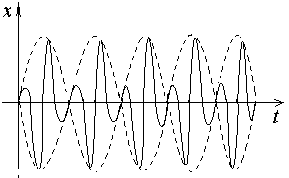
Сложение взаимно перпендикулярных колебаний.

Допустим, что точка может совершать колебательные движения в двух взаимно перпендикулярных направлениях х и у . Пусть начало отсчета по времени выбрано так, что начальная фаза колебания по оси х равна нулю. Таким образом, колебания по х и у можно представить выражениями:

Где  разность фаз между колебаниями по х и по у .

Эти выражения по своей сути являются уравнением траектории движения точки, записанном в параметрическом виде. Найдем уравнение траектории в явном виде .

Для этого преобразуем первое выражение:

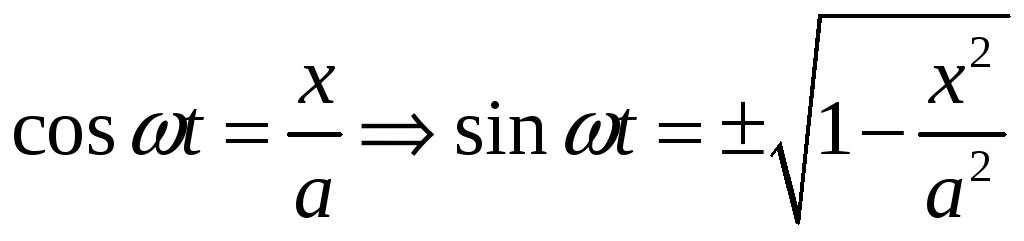
Развернем второе выражение по формуле косинуса суммы двух углов.

Подставим в это уравнение выражение для sint и преобразуем его и получим уравнение эллипса.

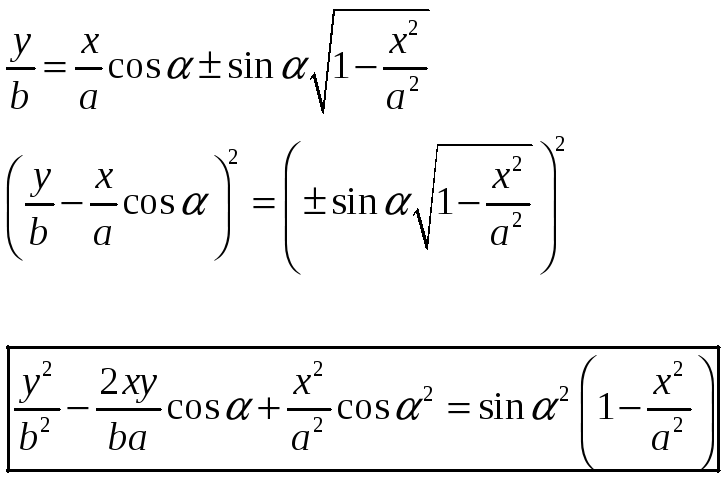
Разберем различные случаи разности фаз между колебаниями.

1.  = 0

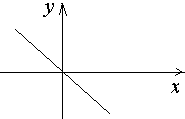
Тогда уравнение траектории превращается в уравнение прямой

2.  = 

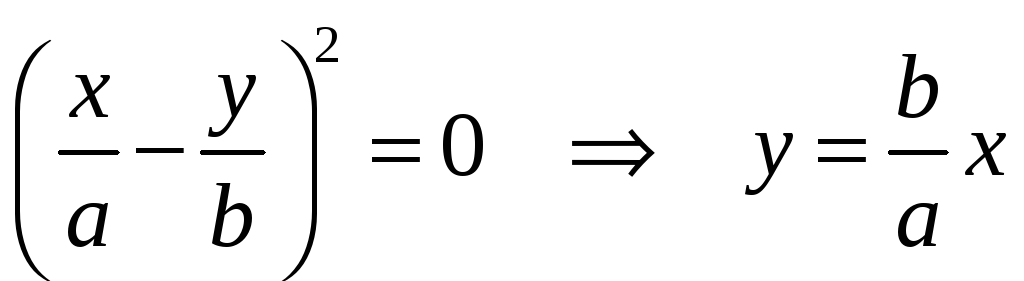
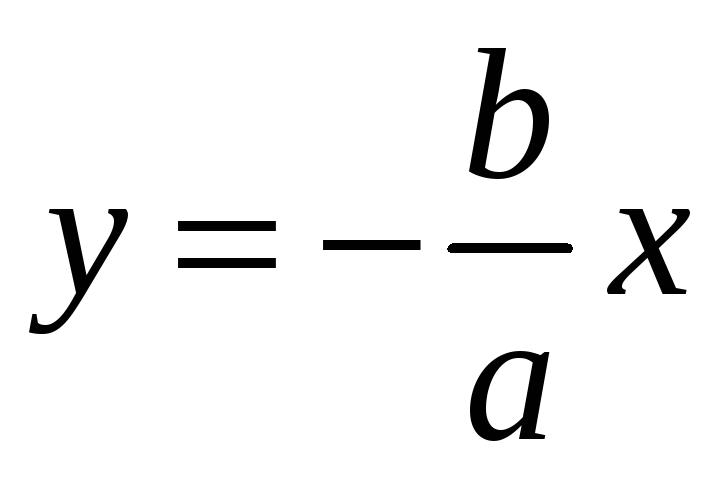
3.  = + /2

Уравнение траектории превращается в уравнение эллипса

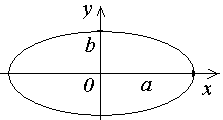
Если  = +/2 то движение точки по элипсной траектории происходит по часовой стрелке.

Если  = -/2 то движение точки по элипсной траектории происходит против часовой стрелке.

В случае, когда частоты взаимно перпендикулярных колебаний отличаются на малую величину  << . Эти колебания можно рассматривать как колебания с одинаковой частотой, но меняющейся во времени разности фаз между колебаниями.

В этом случае результирующее движение происходит по меденно видоизменяющейся во времени кривой

Когда частоты взаимно перпендикулярных колебаний различаются, то результирующее движение может происходить по довольно сложной траектории называемой фигурами Лиссажу.