5. Установочная лекция к модулю №5. Изгиб: прочность, жесткость, энергия, интеграл Мора. Сочетание 2-х прямых изгибов, изгиб с растяжением-сжатием

5.1. Нормальные напряжения при чистом изгибе

Чистым изгибом называется такой вид изгиба, при котором возникает только один внутренний силовой фактор: изгибающий момент. Такой вид деформации возникает, например, при четырехточечном изгибе:

Для случая чистого изгиба справедлива гипотеза Бернулли: сечения, плоские до приложения внешней силы, остаются такими же и после нагружения, поворачиваясь друг относительно друга на некоторый угол.

Для определения напряжений рассмотрим три стороны задачи. 1. Статическая сторона задачи.

Воспользуемся интегральными уравнениями равновесия (1.6) и (1.7):

2. Геометрическая сторона задачи.

Вырежем из балки элемент длиной dz. После приложения нагрузки он выглядит следующим образом:

ρ - радиус нейтральной линии. Нейтральной линией называется след нейтрального слоя, разделяющего балку на области растяжения и сжатия.

dθ - угол поворота сечения.

ab = dz – длина нейтральной линии для выбранного элемента.

50

Выделим волокно длиной a1b1 на расстоянии y от нейтральной линии. До деформации его длина равнялась ab. Относительное изменение длины волокна:

3. Физическая сторона задачи.

Запишем закон Гука в напряжениях и деформациях:

Произведение EJx называется жесткостью поперечного сечения при изгибе.

Подставим (5.5) в (5.4):

Таким образом, абсолютная величина напряжения тем выше, чем больше расстояние y от нейтральной линии. Максимальное напряжение:

где ymax – расстояние от нейтральной линии до наиболее удаленной точки сечения. Введем следующее обозначение:

Для отыскания положения нейтральной линии в области поперечного сечения привлечем оставшиеся два интегральных уравнения равновесия (5.1):

откуда Sx=0, т.е. ось x является центральной.

51

Вывод: нейтральная линия является главной центральной осью поперечного сечения.

Для случая прямоугольного сечения можно утверждать, что ось x – нейтральная.

Таким образом, в отличие от случая растяжения-сжатия, где напряжение постоянно в любой точке поперечного сечения, при чистом изгибе напряжение по высоте сечения изменяется по линейному закону.

5.2. Особенности расчета на прочность балок из пластичных и хрупких материалов

При проектировании элементов конструкции, работающих на изгиб целесообразно использовать сечения с размерами, удовлетворяющими условиям:

σmaxс=[σ]c…..σmaxρ=[σ]ρ

где σmaxс и σmaxρ – напряжения в наиболее удаленных от нейтральной линии точках сечения, соответственно для сжатой и растянутой его части.

Пластичный материал

Для пластичного материала [σ]ρ=[σ]c. В данном случае рационально использовать симметричные профили (при этом σmaxρ=σmaxс).

Экономичными являются профили с уменьшенной металлоемкостью в области нейтральной линии, такие как двутавр и швеллер. Показателем экономичности является удельный момент

Сечение следует располагать таким образом, чтобы силовой фактор действовал в плоскости максимальной жесткости.

52

вести по формуле (5.7).

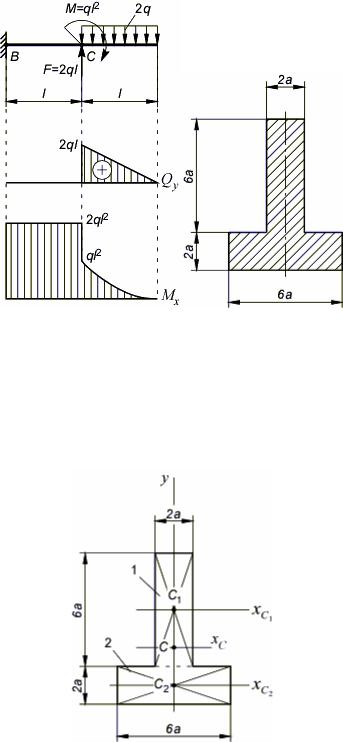
Задача. Подобрать для данной балки размер поперечного сечения a. q=10 кН/м, l=1 м.

Материал балки хрупкий, [σ]ρ=100 МПа, [σ]с=300 МПа.

1.Определяем положение опасного сечения. Для этого строим эпюры поперечной силы Qy и изгибающего момента Mx. По эпюре Mx заключаем, что опасным является участок BC

c M xmax = 2ql2 = 20 кН м. Вид деформации на участке BC – чистый изгиб.

2.Определяем положение опасного волокна в опасном сечении.

Сначала найдем положение точки центра тяжести сечения (это даст положение нейтральной линии).

Разделяем сечение на два прямоугольника с центрами тяжести в точках C1 и C2. Выберем вспомогательную ось совпадающей с центром тяжести одной из фигур (ось xC2 ).

Статический момент сечения относительно вспомогательной оси находим как сумму статических моментов составляющих фигур относительно этой оси:

54

По эпюре Mx находим, что нижняя относительно нейтральной линии часть сечения испытывает сжатие (эпюра Mx строится на растянутом контуре):

Так как σ max p > σ max c , а [σ]ρ<[σ]с, то заданное расположение профиля на опорах нерационально. Целесообразно повернуть сечение на 180º.

Определяем, какие волокна являются опасными. Сравним отношение расстояний до наиболее удаленных сжатого и растянутого волокон с отношением соответствующих допускаемых напряжений:

следовательно, опасны растянутые волокна, и условие прочности следует записать в виде

где J xC - момент инерции поперечного сечения относительно нейтральной линии (главный центральный момент инерции).

Момент инерции J xC определяем как сумму моментов инерции простых фигур, составляющих сечение, относительно главной центральной оси.

Для фигуры 1, используя формулу (4.4):

55