10.2.3Моделирование arc-фильтров на операционных усилителях

10.2.3.1 Проектирование ARC-фильтров на операционных усилителях основывается на последовательном включении развязанных звеньев порядка не выше второго. Поэтому для реализации фильтра высокого порядка функцию его передачи следует представить в виде произведения сомножителей, функции передачи каждого из которых не выше второй.

10.2.3.2 Вывод соотношений для звена с многопетлевой ОС

Как правило, с помощью одного операционного усилителя (ОУ) и RCэлементов в цепи обратной связи реализуют (создают) звено, обладающее функцией передачи второго порядка. Пример звена с многопетлевой обратной связью показан на рис. 10.19.

Рис. 10.19

Для составления функции передачи звена используем законы Кирхгофа.

Например, сумма токов втекающих в узел «2» должна равняться нулю. Будем для определенности токи, втекающие в узел записывать со знаком «-», а вытекающие — со знаком «+»:

(10.2)

Потенциал инвертирующего входа ОУ (рис. 10.19,а) близок к потенциалу неинвертирующего. Разница равна. ЕслиКстремится к бесконечности (а реальные значения составляютК= 20 000), потенциал инвертирующего входа стремится к нулю.

Тогда сумма падений напряжений на сопротивлении z₃и на выходе ОУ должна равняться нулю:

(10.3).

Аналогично: (10.4)

Но иможно связать также просуммировав падения напряжений по контуру z₂, z₄,u_ВЫХ(сумма падений напряжений по контуру равна нулю):

(10.5)

Аналогично, для контура :

, (10.6)

но , откуда(10.7)

Используя (10.3) и (10.4) получим:

(10.8)

Выразив u₂из (10.6) и подставив в (10.8) получим:

(10.9)

Теперь необходимо из (10.4), (10.5), (10.7) выразить токи (i₂,i₃,i₄,) и подставить в (10.2):

(10.10)

(10.11)

, откуда:

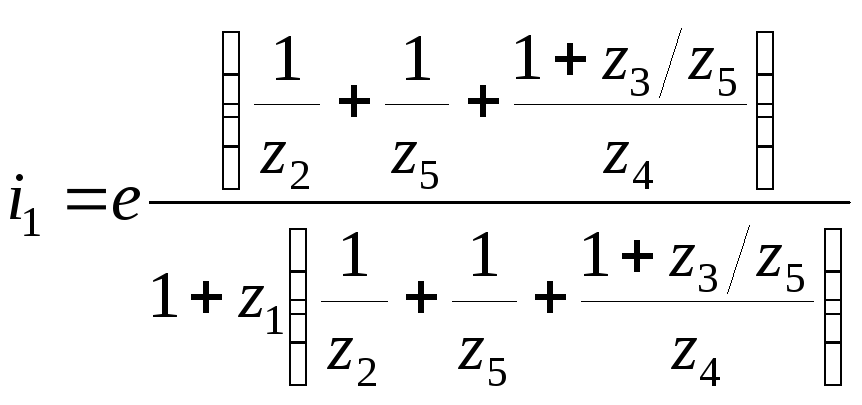(10.12)

Подставив (10.12) в (10.9) получим:

(10.13)

Теперь можно получить выражения для функций передачи звеньев с различными АЧХ.

10.2.3.3 Например, звено, изображенное на рис. 10.20 является звеном ФНЧ.

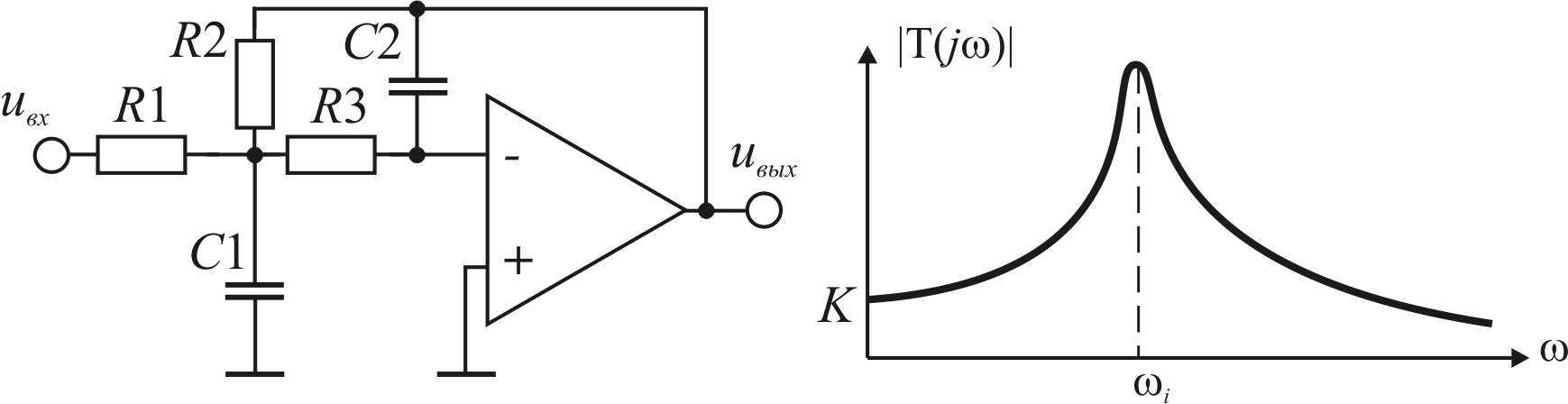
Рис. 10.20 Звено ФНЧ на ОУ с многопетлевой ОС и его АЧХ

Для этой схемы: z₁=R₁,z₂= ,z₄=R₂,z₅=R₃,z₃=. После подстановки функция передачи:

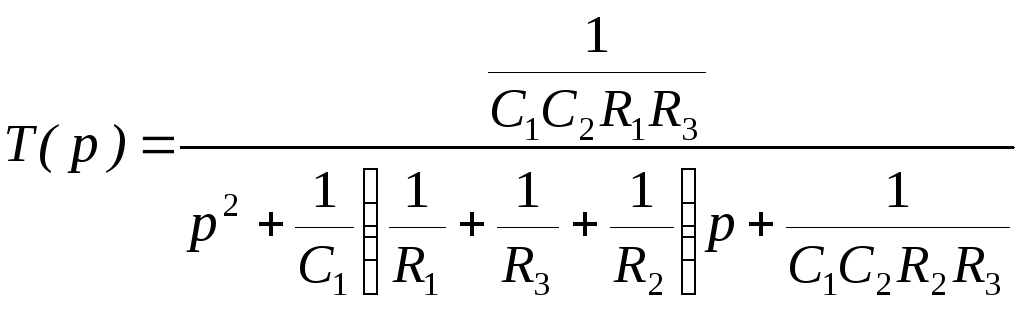. (10.14)

Отнормируем функцию (10.14), поделив ее числитель и знаменатель на квадрат частоты среза ФНЧ:

, (10.15)

здесь – нормированная частотная переменная,,

(10.16)

— коэффициент передачи на постоянном токе,

С =, (10.17)

B =(10.18)

— коэффициенты полинома знаменателя.

При значении частот p,s стремящихся к нулю, функции (10.14) и (10.15) стремятся к значению.

Для того чтобы определить значения элементов R₁,R₂,R₃,C₁,C₂необходимо сопоставить величины коэффициентов при первой степени частоты и свободного члена с величинами коэффициентов сомножителей второго порядка для фильтров с требуемыми функциями передачи, например, с функциями фильтров при аппроксимации по Баттерворту или Чебышеву.

10.2.3.4 При аппроксимации квадрата АЧХ по Баттерворту идеальная прямоугольная характеристика (показана на рис 1.8 тонкой линией) заменяется максимально-гладкой кривой.

, (10.19)

где n — порядок аппроксимирующей функции.

Для оценки затухания вносимого фильтром в полосе задерживания удобнее использовать функцию обратную (10.19) и оценивать затухание в дБ:

(10.20)

На частоте среза фильтра = 1 затуханиеА составляет 3 дБ, что соответствует уменьшению АЧХ в 0,707 раз. Примеры функций затухания фильтров пятого порядка (n = 5) с Баттервортовской и Чебышевской характеристиками приведены на рис. 10.21.

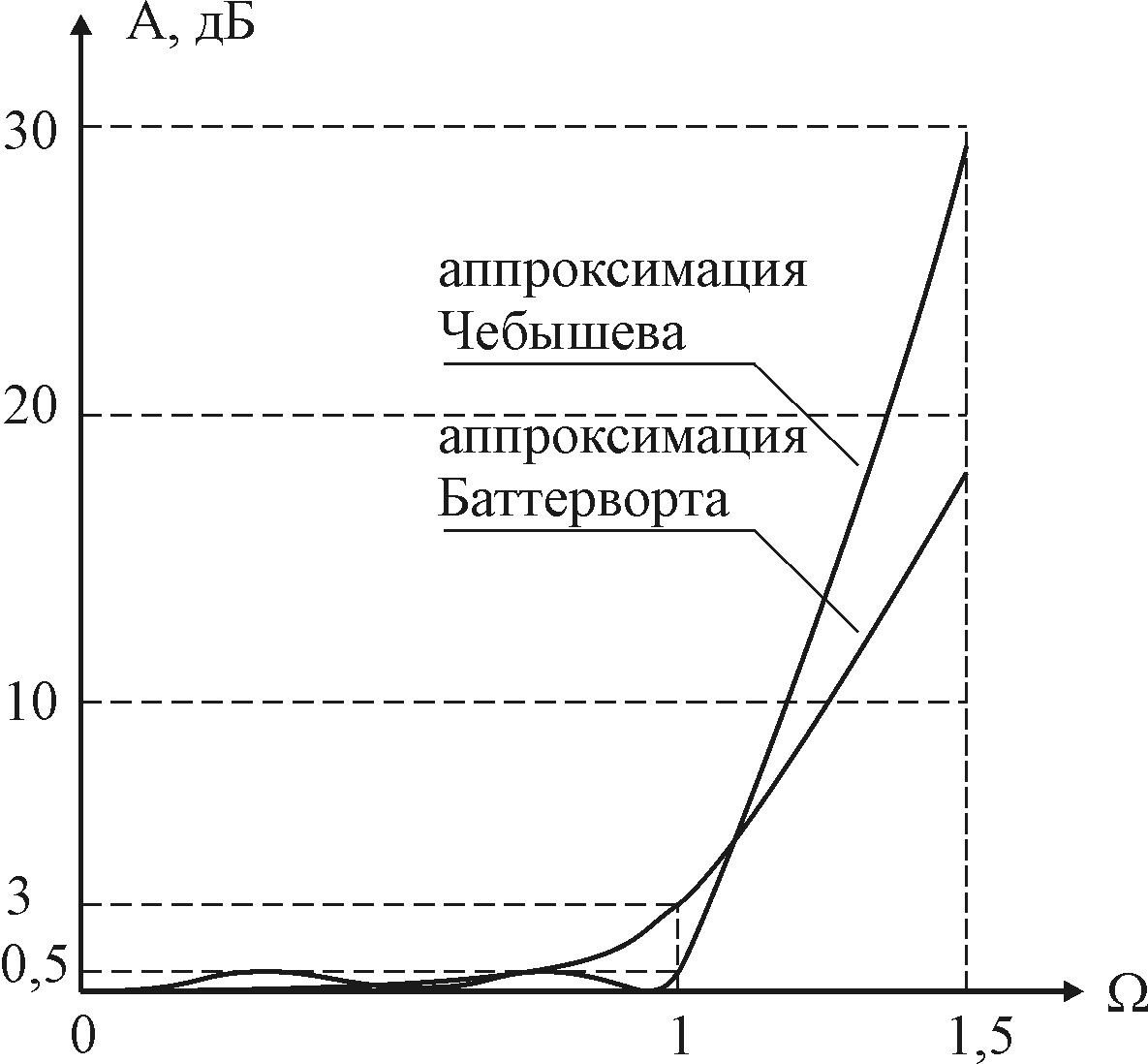
Рис. 10.21 Характеристики затухания фильтров Баттерворта и Чебышева пятого порядка (n = 5)

Функцию передачи ФНЧ при аппроксимации по Баттерворту (в соответствии с соотношениями (1.25—1.27) и (10.19)) можно представить в виде

, (10.21)

либо как произведение сомножителей для n= 2, 4, 6,…:

, (10.22)

или для n= 3, 5, 7,…:

(10.23)

Коэффициенты b_k при любом значенииkопределяются по соотношению:

(10.24)

Примеры сомножителей функций передач ФНЧ при аппроксимации их АЧХ по Баттерворту приведены в таблице 10.3. В соотношении (10.15) значения B выбираются равнымиb_k,С — равными 1 (см. табл. 10.3).

Таблица 10.3

n	Сомножители функции передачи при аппроксимации по Баттерворту
2	s2+1,4142s +1
3	(s+1)(s2 +s +1)
4	(s2+0,7654s +1)(s2 +1,8478s + 1)
5	(s + 1)(s2 +0,6180s +1)(s2 +1,6180s + 1)
6	(s2 +0,5176s +1)(s2 +1,4142s + 1) (s2 +1,9319s +1)
7	(s +1) (s2 +0,4450s +1)(s2 +1,2470s + 1) (s2 +1,8019s +1)
8	(s2 +0,3902s +1)(s2 +1,1111s + 1) (s2 +1,6629s +1) (s2 +1,9616s +1)
9	(s +1) (s2 +0,3473s +1)(s2 +s + 1) (s2 +1,5321s +1) (s2 +1,8794s +1)
10	(s2+0,3129s+1)(s2+0,9080s+1) (s2+1,4142s+1)(s2+1,7820s+1)(s2+1,9754s +1)

10.2.3.5 При аппроксимации квадрата АЧХ по Чебышеву:

, (10.25)

где — полином Чебышеваn-ного порядка.

В полосе пропускания функция квадрата АЧХ изменяется между значениями 1 и (рис. 10.22). Неравномерность АЧХ отсчитывается либо в разах с помощью параметра, либо с помощью параметраAв дБ [12].

, (10.26)

или (10.27)

Рис. 10.22 Параметры АЧХ и коэффициента отражения

Полюсы передаточной функции T(p), расположенные в левой полуплоскости определяются по соотношениям [12]:

p_k= (10.28)

где k= 1, 2, 3,…,n,

; ; (10.29)

Связь параметров ,и максимального в полосе пропускания значения коэффициента отраженияГ_МАКСприведена в табл. 10.4.

Таблица 10.4

AдБ		ГМАКС=
0,1	0,02276	0,15086
0,2	0,045007	0,212148
0,5	0,10875	0,32977
1,0	0,205671	0,4535

Значения иприведены в табл. 10.5.

Таблица 10.5

n	А = 0,1 дБ		А = 0,2 дБ		А = 0,5 дБ		А = 1,0 дБ
2	1,67750	1,95295	1,36265	1,69021	1,0080	1,4199	0.7762	1.26590
3	0,96940	1,39274	0,81463	1,28981	0,6264	1,1800	0.4942	1.11543
4	0,69027	1,21510	0,58746	1,15978	0,4582	1,0999	0.3646	1.06440
5	0,53891	1,13597	0,46138	1,10130	0,3623	1,0636	0.2895	1.04106
6	0,44314	1,09378	0,38067	1,07000	0,3000	1,0440	0.2402	1.02845
7	0,37677	1,06862	0,32431	1,05127	0,2561	1,0322	0.2054	1.02087
8	0,32795	1,05240	0,28265	1,03918	0,2236	1,0246	0.1794	1.01597
9	0,29046	1,04133	0,25057	1,03091	0,2031	1,0204	0.1593	1.01261
10	0,26074	1,03343	0,22507	1,02501	0,1783	1,0157	0.1433	1.01021

Таблицы сомножителей функций передачи, составленные с помощью соотношения (10.28) для значений неравномерности A = 0,1 0,2 0,5 1,0 дБ приведены в таблицах 10.6, 10.7, 10.8, 10.9.

Таблица 10.6

n	Сомножители функции передачи при аппроксимации по ЧебышевуА = 0,1дБ
2	s2+2,3723s +3,314
3	(s+0,9694)(s2 + 0,9694s+1,6897)
4	(s2+0,5283s+1,3300)(s2+1,2754s+ 0,6229)
5	(s+ 0,5389)(s2+0,3330s+1,1949)(s2+0,8719s+ 0,6359)
6	(s2 +0,2294s+1,1294)(s2+0,6267s + 0,6964) (s2 +0,8560s +0,2633)
7	(s +0,3768) (s2 +0,1676s +1,0924)(s2 +0,4698s + 0,7532)(s2 +0,6789s +0,3302)
8	(s2+0,1279s+1,0695)(s2+0,3644s+ 7989) (s2+0,5453s+0,4162)  (s2+0,6433s+0,1456)
9	(s+0,29046) (s2+0,10087s+1,05421)(s2+0,29046s+ 0,8344) (s2+0,4450s+0,4975) (s2 +0,5459s +0,2013)
10	(s2+0,08158s+1,04351)(s2+0,2367s+0,8618) (s2+0,3687s+0,5679)(s2+0,4646s+0,2740)(s2+0,5150s +0,09245)

Таблица 10.7

n	Сомножители функции передачи при аппроксимации по ЧебышевуА = 0,2дБ
2	s2+1,927s+2,356
3	(s+0,8146)(s2 +0,8146s+1,4136)
4	(s2+0,44958s+1,19861)(s2+0,8307s+ 0,3695)
5	(s+ 0,461382)(s2+0,2851s+0,94325)(s2+0,7463s+ 0,6091)
6	(s2 +0,19705s +1,0505)(s2 +0,5383s + 0,6449) (s2 +0,73539s +0,2119)
7	(s+0,32431)(s2+0,1443s+1,0547)(s2+0,4044s+0,7164)(s2+0,5844s+0,2934)
8	(s2+0,11103s+1,04183)(s2+0,31407s+0,7712)(s2+0,4700s+0,3887) (s2+0,5544s+0,1179)
9	(s+0,25056)(s2+0,08702s+1)(s2+0,25057s+0,81278) (s2+0,43399s+0,31278) (s2 +0,47091s +0,17976)
10	(s2+0,07042s+1,0262)(s2+0,20436s+0,84455)(s2+0,3183s+0,55065)  (s2+0,4011s+0,2567)(s2+0,4446 s+0,07513)

Таблица 10.8

n	Сомножители функции передачи при аппроксимации по ЧебышевуА = 0,5 дБ
2	s2+1,4256s+1,5162
3	(s+0,6264)(s2 + 0,6264s+1,1424)
4	(s2+0,3507s+1,0635)(s2+0,8467s+ 0,3564)
5	(s+ 0,3623)(s2+0,2239s+1,0358)(s2+0,5862s+ 0,4767)
6	(s2 +0,1553s +1,02302)(s2 +0,4243s + 0,590) (s2 +0,5795s +0,1570)
7	(s +0,2562) (s2 +0,1140s +1,0161)(s2 +0,3194s + 0,6768)(s2 +0,4616s +0,2538)
8	(s2+0,08724s+1,0119)(s2+0,2484s+ 0,7413) (s2+0,3718s+0,3536) (s2+0,4386s+0,0880)
9	(s+0,1984) (s2+0,06890s+1,0092)(s2+0,1984s+ 0,7893) (s2+0,3039s+0,4525) (s2 +0,3729s +0,1563)
10	(s2+0,05580s+1,0073)(s2+0,1619s+0,8257)  (s2+0,2522s+0,5318)(s2+0,3178s+0,2379)(s2+0,3523s+0,05628)

Таблица 10.9

n	Сомножители функции передачи при аппроксимации по ЧебышевуА = 1,0 дБ
2	s2+1,0977s+1,1025
3	(s+0,4942)(s2 + 0,4942s+0,9942)
4	(s2+0,2791s+0,9865)(s2+0,6737s+ 0,2794)
5	(s+ 0,2895)(s2+0,1789s+0,9883)(s2+0,4684s+ 0,4293)
6	(s2 +0,1243s +0,9907)(s2 +0,3397s + 0,5577) (s2 +0,4641s +0,1247)
7	(s+0,2054) (s2+0,0914s+0,9927)(s2+0,2561s+0,6534)  (s2+0,3701s+0,2304)
8	(s2+0,07001s+0,9941)(s2+0,1964s+ 0,7235) (s2+0.2984s+0,3408) (s2+0,3520s+0,07026)
9	(s+0,1593) (s2+0,05533s+0,9952)(s2+0,1593s+ 0,7754) (s2+0,2441s+0,4385) (s2 +0,2994s +0,1423)
10	(s2+0,04483s+0,9960)(s2+0,1301s+0,8144)(s2+0,2026s+0,5205) (s2+0,2553s+0,2266)(s2+0,2830s +0,0450)

В соотношении (10.15) значения BиС выбирается из табл. 10.6—10.9.

Итак, в общем случае, полином знаменателя сомножителя функции передачи имеет вид . Сопоставляя коэффициентыВ,Сиз таблиц и соотношения (10.15)найдем соотношения для расчета величины элементовR₁,R₂,R₃,C₁,C₂звена активного фильтра.

Выразим R₁из (10.16) и подставим в (10.17):

(10.30)

Выразим 1/R₃из (10.30) и подставим в (10.18):

или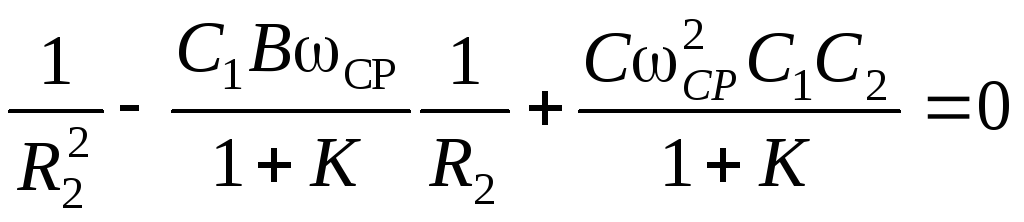

откуда

или 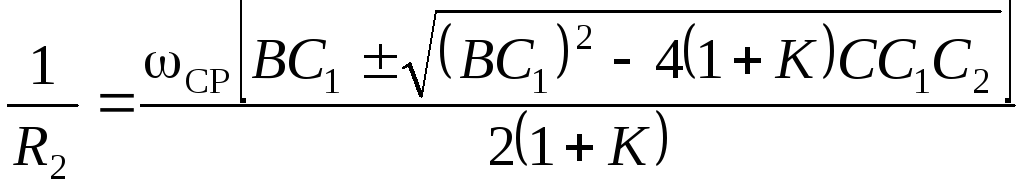(10.31)

В простейшем случае при К=1, R₁=R₂. Из (10.31):

(10.32)

или (10.33)

При выполнении равенства (10.33)(10.34)

Из (10.16) (10.35)

Пример расчета и моделирования ФНЧ восьмого порядка n = 8 при аппроксимации по Баттерворту. Выпишем сомножители функции передачи из таблицы 10.3:

Таким образом, фильтр будет содержать четыре звена по схеме рис. 10.20 включенные последовательно. Зададим частоту среза фильтра, например, f_СР = 10 кГц и выберем «произвольно» значение емкостейC₂₁=C₂₂=C₂₃=C₂₄= = 2 нФ.

Здесь C₂₁ = C₂₂ = C₂₃ = C₂₄ — значения емкостей C₂ соответственно в первом, втором, третьем и четвертом звене.

Далее рассчитываем значения емкости С₁₁, резисторов R₁₁ и R₃₁ для первого звена по соотношениям (10.33), (10.34), (10.35). Значение В₁ = b₁ = 0,3902; С₁ = 1.

нФ,

кОм

Ом

Аналогичным образом рассчитываем значения емкостей и конденсаторов для второго, третьего и четвертого звеньев (при этом В₂ = b₂ = 1,1111; В₃ = b₃ = 1,6629; В₄ = b₄ = 1,9616; С₂ = С₃ = С₄ = 1):

С₁₂ = 12,96 нФ, С₁₃ = 5,78 нФ, С₁₄ = 4,16 нФ;

R₁₂ = 4,42 кОм, R₁₃ = 6,62 кОм, R₁₄ = 7,81 кОм;

R₃₂ = 2,21 кОм, R₃₃ = 3,31 кОм, R₃₄ = 3,902 кОм,

Схема фильтра, в пакете OrCad, изображена на рис. 10.23, частотные характеристики — на рис. 10.24.

Рис. 10.23

Рис. 10.24