
Teoria_uprugosti_Ch1_Ledovskoy_12
.pdf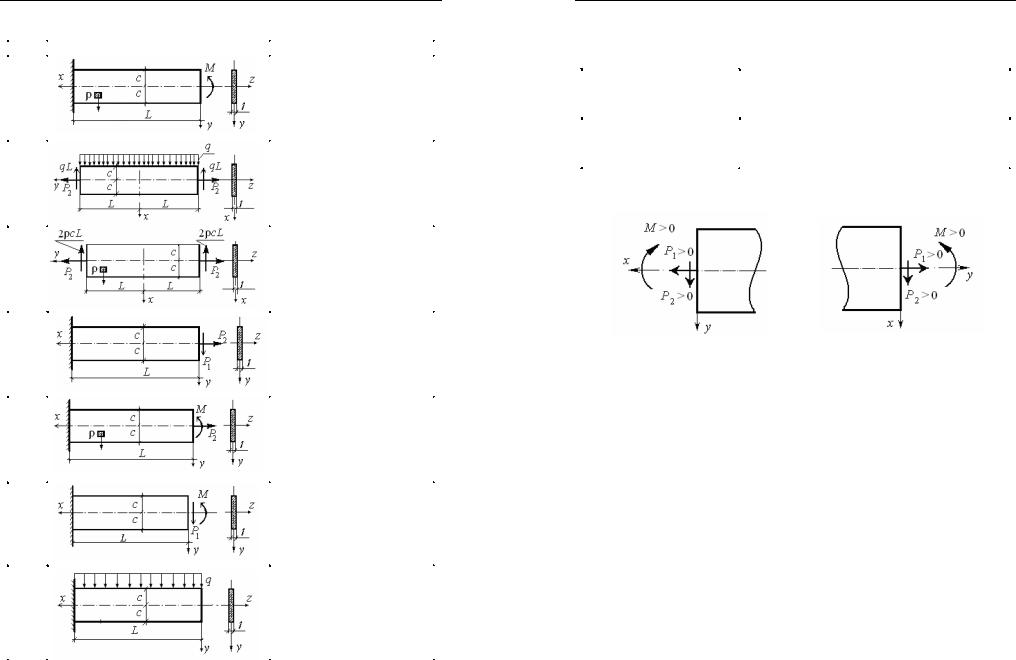
Теория упругости. Часть I
Окончание табл. 4.1
1 |
2 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|||
86÷87 |
|
ϕ= b3 x2 y + d3 y3 |
+ a2 |
|
x2 + |
|
||||||||||||||||||
|
|
+ d5 |
2 |
|
|
|
|
6 |
|
|
|
|
2 |
|
|
|
|
|
||||||
|
|
|
(x2 y3 |
− 1 y5) |
|
|
|
|
|
|
|
|
||||||||||||
|
|
6 |
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
88÷89 |
|
ϕ= d5 |
(y2x3 − |
1 x5)+ c2 |
x2 |
+ |
||||||||||||||||||
|
|
|
b |
|
6 |
|
|
d |
2 |
|
|
|
5 |
d |
3 |
|
2 |
|
|
|||||
|
|
+ 3 |
|
|
xy2 + |
|
|
|
y |
2 + |
|
|
|
x3 |
|
|
||||||||
|
|
|
2 |
|
2 3 |
|
|
|||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
90÷91 |
|
ϕ= d5 |
(y2x3 − |
1 x5)+ |
|
|
|
|
||||||||||||||||
|
|
|
b |
|
6 |
|
|
d |
|
|
|
|
5 |
c |
|
|
|
|
|
|
|
|||
|
|
|
|
|
xy2 + |
3 x3 + |
2 |
x2 |
|
|
||||||||||||||
|
|
+ 3 |
|
|
|
|
|
|
|
|||||||||||||||
|
|
2 |
|
|
|
|
|
6 |
|
|
|
|
|
2 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
92÷93 |
|
ϕ=b xy + d4 xy3 + c2 y2 |
|
|
||||||||||||||||||||
|
|
|
|
|
2 |
|
|
6 |
|
|
|
|
|
|
2 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
94÷95 |
|
ϕ= |
|
|
b3 |
|
y3 |
+ |
c2 |
y2 |
+ |
d3 |
x2 y + |
|||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
2 3 |
|
|
2 |
|
|
|
|
2 |
|
|
|
|
||||||||
|
|
+ |
|
d5 |
(x2 y3 − |
|
1 y5) |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||||||||||||||||
96÷97 |
|
ϕ= b3 y3 + |
d4 |
xy3 +b xy |
|
|
||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
6 |
|
|
|
|
6 |
|
|
|
|
|
2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
||||||||||||||||||
98÷99 |
|
ϕ= a2 |
x2 + b3 x2 y + d3 |
|
y3 + |
|
||||||||||||||||||
|
|
|
d5 |
2 |
|
|
|
|
2 |
|
|
|
|
|
6 |
|
|
|
|
|
||||
|
|
+ |
|
(x2 y3 |
− 1 y5) |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
6 |
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача 4. Плоская задача теории упругости. Функция напряжений
|
|
|
|
|
|
|
|
|
|
|
Таблица 4.2 |
|||||
ИнтегральныеграничныеусловияпоСен-Венану |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
Ось x параллельна |
c |
c |
c |
|
||||||||||||
длинной стороне полосы |
M = ∫ |
|
|
y dy; |
P2 = ∫ |
|
|
dy; |
|
|
|
|
|
|
||
|
|
|
|
P1 = ∫Y |
dx |
|
||||||||||
X |
X |
|||||||||||||||
(рис. 9) |
−c |
−c |
−c |
|
||||||||||||
Ось y параллельна |
c |
c |
c |
|
||||||||||||
|
|
|
|
x dx; |
|
|
|
dx; |
P1 = ∫ |
X |
dx |
|
||||
длинной стороне полосы |
M = ∫Y |
P2 = ∫Y |
|
|||||||||||||
(рис. 10) |
−c |
−c |
−c |
|
||||||||||||
Рис. 9 |
Рис. 10 |
Примечание. На рис. 9 и 10 равнодействующие внутренних усилий имеют положительные значения.
40 |
41 |
Теория упругости. Часть I
Задача 5. РАСЧЕТ ТОНКИХ ПЛИТ ПРИ ПОПЕРЕЧНОМ ИЗГИБЕ
Функция прогибов w срединной поверхности плиты выбирается по шифру из табл. 5.1
Для этой функции требуется определить:
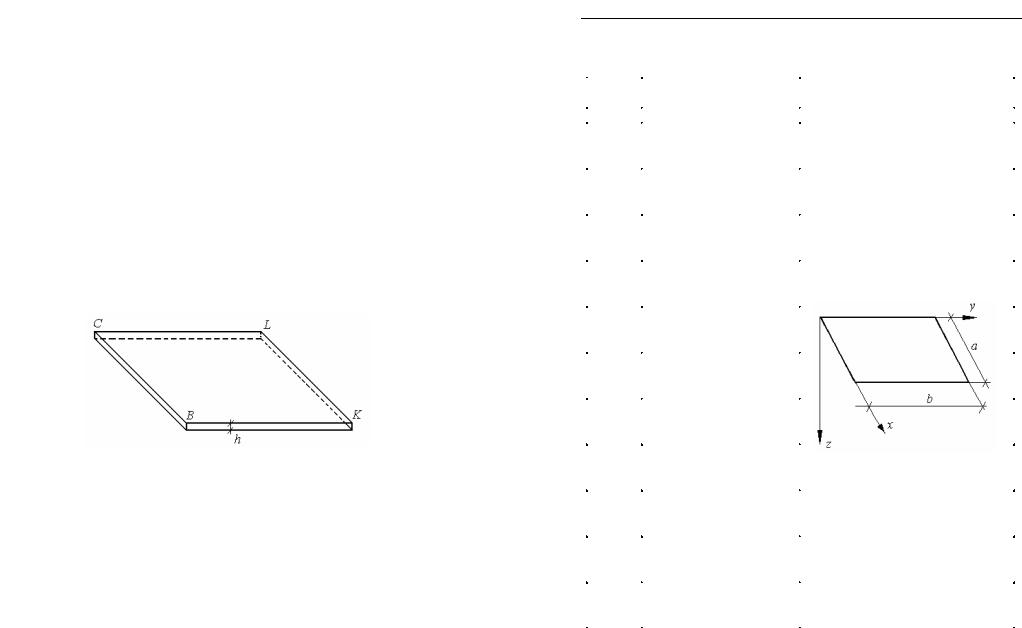
•закрепление по контуру плиты (рис. 11);
•интенсивностьираспределениевнешнейнагрузки,приложенной перпендикулярно срединной плоскости плиты;
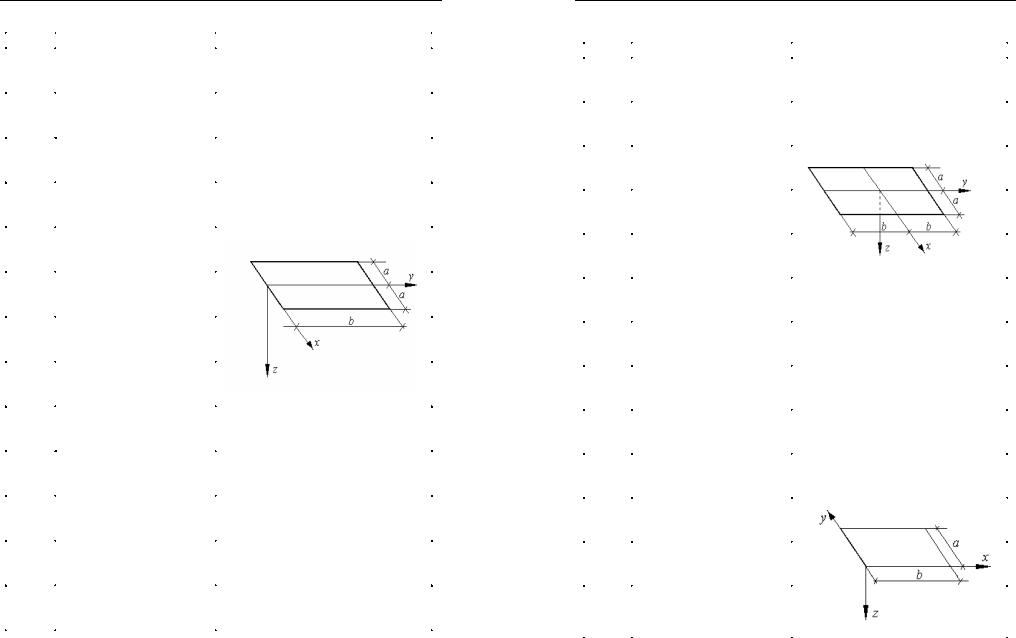
•распределение активных и (или) реактивных погонных усилий на двух краях плиты (табл. 5.1), а также начертить эпюры этих усилий;
•погонные усилия в окрестностях точки с координатами, указанными в табл. 5.2.
Рис. 11
Задача 5. Расчет тонких плит при поперечном изгибе
Таблица 5.1
Исходные данные к задаче 5
Буквы |
Функции прогибов |
|
Расчетная схема плиты |
|||||
AB |
|
|||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
3 |
|
00÷01 |
w = Ax2 y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
02÷03 |
w = A(x −a)2 y2 |
|
|
|
|
|||
|
|
|
|
|
|
|||
04÷05 |
w = Ax2 (y −b)2 |
|
|
|
|
|||
|
|
|
|
|||||
06÷07 |
w = A(x −a)2 (y −b)2 |
|
|
|||||
|
|
|
|
|
|
|
||
08÷09 |
w = Ax2 sin |
πy |
|
|
|
|
||
|
|
|
b |
|
|
|
|
|
10÷11 |
w = Ay2 sin |
πx |
|
|
|
|
||
|
|
|
a |
|
|
|
|
|
12÷13 |
w = A(y −b)sin |
πx |
|
|
||||
|
|
|
|
|
|
a |
|
|
14÷15 |
w = A(x −a) |
2 |
sin |
πy |
|
|
||
|
b |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
16÷17 |
w = Asinπx sin πy |
|
|
|||||
|
a |
|
|
|
b |
|
|
|
18÷19 |
w = Ax2 y(y −b) |
|
|
|
|
|||
|
|
|
|
|||||
20÷21 |
w = A(x2 −a2 )sin πy |
|
|
|||||
|
|
|
|
|
|
b |
|
|
42 |
43 |
Теория упругости. Часть I
|
|
|
|
|
|
Продолжение табл. 5.1 |
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
3 |
|
||
22÷23 |
w = Acos n πx sin |
πy |
|
|
|||
|
|
a |
|
b |
|
|
|
24÷25 |
w = A(x −a)2 sin |
πy |
|
|
|||
|
|
|
|
|
b |
|
|
26÷27 |
w = A(y2 − yb)cos πx |
|
|
||||
|
|
|
|
|
2a |
|
|
28÷29 |
w = A(x2 −a2 )y2 |
|
|
|
|||
|
|
|
|
|
|
||
30÷31 |
w = A(x2 −ax)(y −b)y |
|
|
||||
|
|
|
|
|
|
|
|
32÷33 |
w = Ay2 cos πx |
|
|
|
|
||
|
|
2a |
|
|
|
|
|
34÷35 |
w = A(x −a)2 sin |
πy |
|
|
|||
|
|
|
|
|
b |
|
|
36÷37 |
w = Ay2 (x2 −a2 ) |
|
|
|
|||
|
|
|
|
|
|
||
38÷39 |
w = A(x2 −a2 )(y2 −b2 ) |
|
|
||||
|
|
|
|
|
|
|
|
40÷41 |
w = Acos |
πx |
cos |
πy |
|
|
|
|
2b |
|
|
||||
|
|
2a |
|
|
|||
42÷43 |
w = A(x −a)2 (y −b)2 |
|
|
||||
|
|
|
|
|
|||
44÷45 |
w = A(x + a)2 cos |
πy |
|
|
|||
|
|
|
|
|
2b |
|
|
46÷47 |
w = A(x2 −a2 )sin πy |
|
|
||||
|
|
|
|
|
b |
|
|
Задача 5. Расчет тонких плит при поперечном изгибе
|
|
|
|
|
|
|
|
|
Продолжение табл. 5.1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
3 |
|
48÷49 |
w= Acos |
πx |
|
|
πy |
|
|
|
||
|
1+cos |
|
b |
|
|
|
||||
|
|
2a |
|
|
|
|
|
|
||
50÷51 |
w = A(a2 − x2 )(b2 − y2 ) |
|
|
|
||||||
|
|
|
|
|
|
|
||||
52÷53 |
w = A(x + a)(y2 −b2 ) |
|
|
|
|
|||||
|
|
|
|
|
|
|||||
54÷55 |
w = A(y +b)2 (x2 − a2 ) |
|
|
|
||||||
|
|
|
|
|
|
|
||||
56÷57 |
w = A(x2 − a2 )cos |
πy |
|
|
|
|
||||
|
|
|
|
|
2b |
|
|
|
|
|
58÷59 |
w = A(y2 −b2 )cos |
πx |
|
|
|
|
|
|||
2a |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
60÷61 |
w = A(y2 −b2 )(x2 −a2 ) |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||
62÷63 |
w = A(y − a)2 x2 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
64÷65 |
w = Acos |
πx cos |
πy |
|
|
|
|
|
||
|
|
2a |
2b |
|
|
|
|
|
||
66÷67 |
w = A(x −b)2 (y − a)2 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
68÷69 |
w = Ay2 sin |
πx |
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
70÷71 |
w = Ax2 sin |
πy |
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
72÷73 |
w = A(y − a)sin |
πx |
|
|
|
|
|
|||
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
44 |
45 |
Теория упругости. Часть I
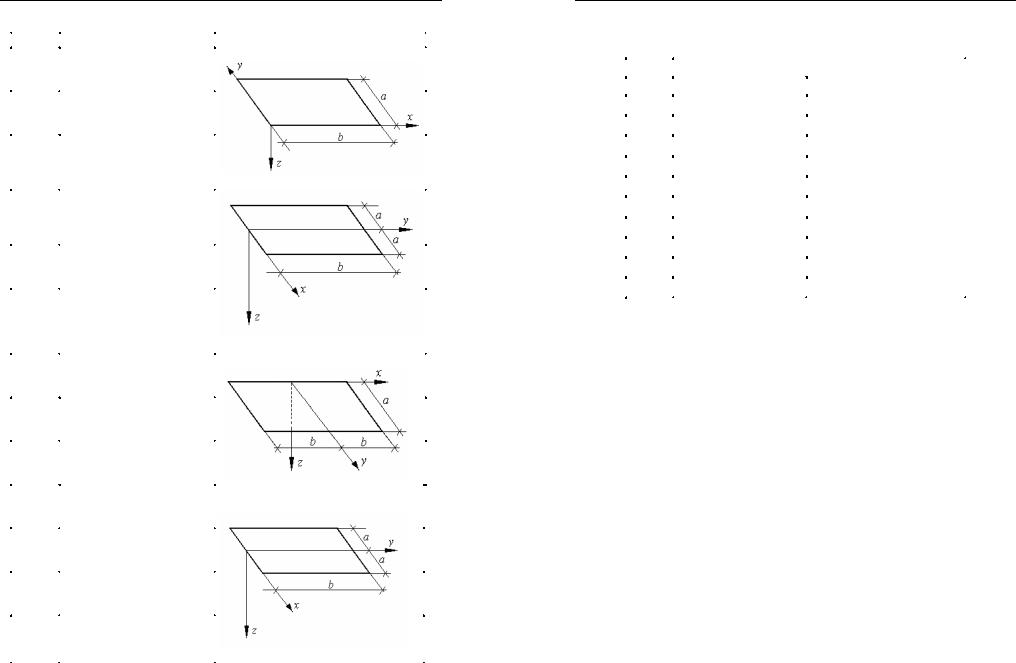
Окончание табл. 5.1
1 |
2 |
|
|
3 |
|
74÷75 |
w = A(x −b)2 sin πy |
|
|
||
|
|
a |
|
|
|
76÷77 |
w = Asin πy sin |
πx |
|
|
|
|
a |
b |
|
|
|
78÷79 |
w = Ay2 x(x −b) |
|
|
|
|
|
|
|
|
|
|
80÷81 |
w = A(y2 −a2 )sin |
πx |
|
|
|
|
|
|
2b |
|
|
|
|
|
|
|
|
82÷83 |
w = Acos πy sin |
πx |
|
|
|
|
2a |
b |
|
|
|
84÷85 |
w = Ay2 sin πx |
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
86÷87 |
w = A(x2 − xb)cos |
πy |
|
|
|
|
|
|
2a |
|
|
88÷89 |
w = A(x2 −b2 )y2 |
|
|
|
|
|
|
|
|
|
|
90÷91 |
w = Ax2 cos πy |
|
|
|
|
|
a |
|
|
|
|
92÷93 |
w = A(x − a)2 y(y −b) |
|
|
||
|
|
|
|
|
|
94÷95 |
w = Ax2 y(y −b) |
|
|
|
|
|
|
|
|
|
|
96÷97 |
w = A(x2 − a2 )y2 |
|
|
|
|
|
|
|
|
|
|
98÷99 |
w = A(x −a)2 y2 |
|
|
|
|
|
|
|
|
|
|
Задача 5. Расчет тонких плит при поперечном изгибе
|
|
|
Таблица 5.2 |
|
|
Определение погонныхусилий в задаче 5 |
|||
|
|
|
|
|
Буква |
Определение усилий |
|
|
|
А |
|
|
|
|
на краях плиты |
в точке с координатами |
|
||
0 |
BC, CL |
x = 0,8a; |
y = 0,2b |
|
|
||||
1 |
CL, LK |
x = 0,5a; y = 0,5b |
|
|
|
||||
2 |
LK, BK |
x =0,2a; |
y = 0,4b |
|
|
||||
3 |
BC, BK |
x =0; y = 0,5b |
|
|
|
||||
4 |
BC, KL |
x =0,4a; |
y = 0,6b |
|
5 |
KL, LC |
x =0; y = 0,5b |
|
|
|
|
|
|
|
6 |
CL, BK |
x =0,5a; |
y =0 |
|
7 |
CL, BC |
x = 0,3a; |
y = 0,2b |
|
|
||||
8 |
BK, KL |
x =0,6a; |
y =0,6b |
|
|
||||
9 |
BC, CL |
x = 0,4a; y =0 |
|
|
|
||||
46 |
47 |

Теория упругости. Часть I |
|
Оглавление |
|
Предисловие .......................................................................................................... |
3 |
Принятые обозначения ......................................................................................... |
4 |
Вопросы для самоконтроля.................................................................................. |
8 |
Введение .............................................................................................................. |
11 |
Задача 1. Исследование напряженно-деформированного состояния |
|
в точке тела .......................................................................................................... |
12 |
Задача 2. Постановка кинематических и статических граничных условий.... |
14 |
Задача 3. Решение простейших задач в теории упругости обратным |
|
методом................................................................................................................ |
20 |
Задача 4. Плоская задача теории упругости. Функция напряжений ............. |
31 |
Задача 5. Расчет тонких плит при поперечном изгибе.................................... |
42 |
Учебное издание
ЛедовскойИгорьВасильевич Рощин Владимир Васильевич Халецкая Ольга Борисовна Шульман Георгий Сергеевич
ТЕОРИЯУПРУГОСТИ
Учебно-методическоепособие
Часть I
Редактор В. А. Преснова Корректоры А. А. Стешко, К. И. Бойкова Компьютерная верстка И. А. Яблоковой
Подписано к печати 10.05.12. Формат 60×84 1/16. Бум. офсетная Усл. печ. л. 2,8. Тираж 500 экз. Заказ 62. «С» 27.
Санкт-Петербургский государственный архитектурно-строительный университет. 190005, Санкт-Петербург, 2-я Красноармейская ул., д. 4.
Отпечатано на ризографе. 190005, Санкт-Петербург, 2-я Красноармейская ул., д. 5.
48
