§ 3. Операции над графами

Удаление вершины или ребра, а также переход к подграфу — это операции, с помощью которых можно из имеющегося графа получать другие графы с меньшим числом элементов. Известны также операции, позволяющие, наоборот, получать из имеющихся графов «большие» графы. Такова, например, операция добавления ребра: если вершины u и v графа G не смежны, то можно определить граф G + e, где e = uv. Он получается из графа G добавлением ребра e.

Здесь рассматриваются другие операции над графами, нужные для дальнейшего изложения.

Одной из наиболее важных является операция объединения. ГрафH называется объединением (или наложением) графов F и G, если VH = VFVG и EH = EFEG (рис. 3.1). В этой ситуации пишут H = FG. Объединение FG называется дизъюнктным, если VFVG = . Аналогично определяются объединение и дизъюнктное объединение любого множества графов, причем в последнем случае никакие два из объединяемых графов не должны иметь общих вершин.

ПустьG_i=(V_i, E_i) (i=l, 2)-два графа. Произведением G₁ * G₂ = G называется граф, для которого VG = V₁*V₂ — декартово произведение множеств вершин исходных графов, a EG определяется следующим образом: вершины (u₁, u₂) и (v₁, v₂) смежны в графе G тогда и только тогда, когда или u₁ = v₁, а u₂ и v₂ смежны в G₂, или u₂=v₂ , a u₁ и v₁ смежны в g₁ (рис. 3.2). Очевидно, что

|G₁*G₂| = |G₁|•|G₂|, |E(G₁*G₂)| = |G₁|•|EG₂| + |G₂|•|EG₁|.

С помощью операции произведения вводится важный класс графов — n-мерные кубы. n-мерный куб Q_n определяется рекуррентно:

Q₁=K₂, Q_n=K₂*Q_n-1, n > 1.

Очевидно, что Q_n - граф порядка 2ⁿ, вершины которого можно представить (0, 1)-векторами длины n таким образом, что две вершины будут смежны тогда и только тогда, когда соответствующие векторы различаются ровно в одной координате. Поскольку каждая вершина n-мерного куба инцидентна n ребрам, то число его ребер равно п2^n-1. На рис. 3.3 представлены кубы Q₂ и Q₃.

Еще одна важная операция — отождествление (или слияние) вершин. Пусть u и v — две вершины графа G, H = G — и — v. К графу H присоединим новую вершину v', соединив ее ребром с каждой из вершин, входящих в объединение окружений вершин u и v в графе G. Говорят, что построенный граф получается из графа G отождествлением вершин u и v.

Р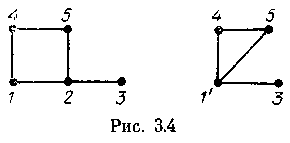ассматривается также операция стягивания ребра.Стягивание ребра uv означает отождествление смежных вершин u и v. На рис. 3.4 показаны граф G и граф, полученный из G стягиванием ребра {1, 2}.

Граф G называется стягиваемым к графу H, если H получается из G в результате некоторой последовательности стягиваний ребер. Легко видеть, например, что граф Петерсена стягиваем к K₅ и, стало быть, к любому K_n с n < 5. Очевидно, что любой непустой связный граф, отличный от K₁, стягиваем к K₂. Но уже не любой связный граф стягивается к графу K₃. Например, простая цепь P_n не стягивается к K₃. Естественно возникает параметр (G)—максимум порядков полных графов, к которым стягивается граф G. Параметр (G) называется числом Хадвигера графа G. Это число связано с проблемой четырех красок (см. § 59).

Вопределенном смысле двойственной к операции стягивания ребра является операция расщепления вершины. Пусть v — одна из вершин графа G. Разобьем ее окружение произвольным образом на две части M и N и выполним следующее преобразование графа G: удалим вершину v вместе с инцидентными ей ребрами, добавим новые вершины u и w и соединяющее их ребро uw, вершину и соединим ребром с каждой вершиной из множества M, а вершину v — с каждой вершиной из множества N. Полученный в результате граф обозначим символом . Будем говорить, что получается из графа G расщеплением вершины v (рис. 3.5).