§ 11. Группа автоморфизмов графа

Характеристикой симметрии графа является его группа автоморфизмов.

Произвольная подстановка  на множестве вершин графа G, сохраняющая отношение смежности, т. е. такая, что образы (u) и (v) вершин u и v смежны тогда и только тогда, когда смежны сами вершины u и v, называется автоморфизмом графа G.

Иными словами, автоморфизм графа — это изоморфизм графа на себя.

Любой граф G имеет по меньшей мере один автоморфизм — тождественное преобразование e: VG -> VG, при котором e(v)=v для любой вершины v. Очевидно, что если  — автоморфизм графа G, то и обратная подстановка ^-1 также является автоморфизмом, если же подстановки  и  обе суть автоморфизмы, то и их произведение  — автоморфизм. Поэтому верно следующее (важное, хотя и очевидное)

Утверждение 11.1. Множество всех автоморфизмов графа относительно операции умножения подстановок является группой.

Группа автоморфизмов графа G обозначается через AutG.

Очевидно также

Утверждение 11.2. Всякий автоморфизм графа G является также автоморфизмом дополнительного графа , т. е.Aut G = Aut .

Поскольку среди двух графов G и хотя бы один является связным, то в силу утверждения 11.2, когда мы имеем дело с группой автоморфизмов, достаточно рассматривать лишь связные графы.

Введем важное понятие орбиты группы подстановок. Пусть Г — произвольная группа подстановок на множестве V. Определим на V бинарное отношение ~, положив u ~ v для u, vV тогда и только тогда, когда в Г существует такая подстановка s, что s(u)=v. Очевидно, что отношение ~ является отношением эквивалентности и, следовательно, множество V разбивается на классы эквивалентных элементов: все элементы, входящие в один класс, переводятся подстановками из группы Г друг в друга, а элементы из разных классов друг в друга не переводятся. Эти классы называются орбитами группы Г. Разбиение множества вершин графа G на орбиты группы Aut G — важная задача. В сущности, применение к графу автоморфизма означает перенумерацию его вершин, причем отношение смежности должно сохраняться. Поэтому для любого автоморфизма  у вершины графа v и ее образа (v) «все одинаково» (степени равны, графы, порожденные окружениями, изоморфны и т. д.). Так что орбиты группы Aut G - это просто классы «одинаковых» вершин. Более того, известно, что проблема распознавания принадлежности двух вершин произвольного графа одной орбите его группы автоморфизмов и проблема изоморфизма графов эквивалентны в том смысле, что любой алгоритм, эффективно решающий одну из этих проблем, может быть преобразован в эффективный алгоритм для другой (см., например [18]). К сожалению эффективные алгоритмы для решения этих двух проблем не известны (о том, какие алгоритмы считаются эффективными, см. гл. XII).

Т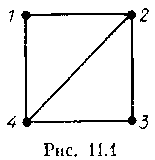рудно сказать что-либо определенное о строениигруппы автоморфизмов произвольного графа. Она может быть и «малой», и «большой». Найдем, например, Aut G для графа G, изображенного на рис. 11.1. Очевидно, что любой автоморфизм либо оставляет неподвижной вершину 1, либо переставляет ее с вершиной 3. В любой ситуации вершины 2 и 4 либо обе неподвижны, либо переводятся друг в друга. Итак, Aut G состоит из четырех элементов: e, транспозиций (1,3) и (2,4) и произведения этих транспозиций — (1,3) (2,4).

Очевидно, что каждый из двух графов, изображенныхна рис. 11.2, имеет лишь один автоморфизм — тождественный. С другой стороны, очевидно, что группой автоморфизмов полного графа K_n является вся симметрическая группа S_n.

С 1936 г. известен следующий вопрос Д. Кёнига: какие конечные группы являются группами автоморфизмов графов? Этот вопрос можно интерпретировать двояким образом. Первый вариант: какие конечные группы изоморфны группам автоморфизмов графов? На этот вопрос почти сразу же ответил Р. Фрухт (1938 г.).

Теорема Фрухта. Каждая конечная группа изоморфна группе автоморфизмов некоторого графа.

> Пусть Г — группа порядка n > 1 (для n = 1 выше приводились примеры). Построим граф G описанным ниже способом. В качество исходного множества вершин возьмем множество всех элементом группы Г. Каждую упорядоченную пару (u, v) несовпадающих вершин соединим простой цепью P_uv длины 3, добавляя всякий раз по две новые вершины a_uv и b_uv: P_uv =(u, a_uv, b_uv, и). Затем к каждой из вершин a_uv «приклеим» простую цепь P(a, u, v) длины l(a, u, v), все вершины которой, исключая a_uv,— новые. Аналогично построим цепи P(b, u, v) длины l(b, u, v). При этом будем соблюдать следующее условие: длины всех цепей попарно различны всегда, кроме случая, когда u^-1v = u₁^-1v₁ , u, v, u₁, v₁Г. В последнем случае должно быть

l(a, u, v)=l(a, u₁, v₁), l(b, u, v) = l(b, u₁, v₁). (1)

Построенный таким образом граф обозначим буквойG. (На рис 11.3 показаны соответствующие графы для n = 2 и 3. В этой ситуации Г — циклическая группа: Г ={v, v² = e} при n = 2, Г = {v, v², v³ = e} при n = 3.)

Докажем, что группы Aut G и Г изоморфны. Вначале фиксируем в Г какой-либо элемент w и следующим образом определим отображение l_w: VG -> VG. Для xГ l_w(x)=wx — произведение элементов группы; вершины цепи P(a, u, v) переводятся в вершины цепи P(a, wu, wv), причем сохраняется последовательность вершин в цепи, т. е. l_w(a_uv) = a_(wu)(wv) и т. д.; аналогично для цепи P(b, wu, wv). Прямая проверка подтверждает, что l_wAut G.

Теперь докажем равенство

Пусть  — произвольный автоморфизм графа G. Очевидно, что  все концевые вершины и, следовательно, все цепи P_uv переводит друг в друга. Поэтому автоморфизм  переставляет друг с другом вершины вида a_uv, а также вершины вида b_uv. Следовательно, и элементы группы Г переставляются друг с другом. При этом из условия (1) следует, что если (u)= u₁, (v)=v₁, то u^-1v = u₁^-1v₁ для всех u, vГ. Из этого равенства, положив (e)= w, получим (x) = wx для любого xГ, т. е.  = l_w. Равенство (2) доказано.

Далее, определим отображение : Г -> Aut G, положив (x) = l_x для любого xГ. Очевидно, что отображение  является изоморфизмом групп Г и Aut G. <

К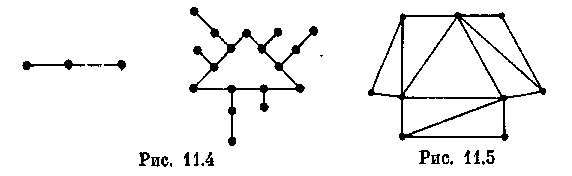онструкция, приведенная в предыдущем доказательстве, неэкономна в том смысле, что приводит к графам с большим числом элементов. Как правило, эти графы можно «уменьшить». Например, при n = 2, 3 вместо графов, приведенных на рис. 11.3. можно взять графы на рис. 11.4. Группой автоморфизмов графа, показанного на рис. 11.5, также является циклическая группа порядка 3.

Можно указать примеры групп подстановок, которые хотя и изоморфны по теореме Фрухта группам автоморфизмов графов, но сами таковыми не являются. Рассмотрим знакопеременную группу A_n, состоящую из всех четных подстановок (n > 3). Пусть A_nAut G. Легко заметить, что группа A_n дважды транзитивна, т. е. для любых i, j, k, lVG, ij, kl, в A_n существует такая подстановка , что (i)= k, (j)=l. Если  — автоморфизм некоторого графа G, то в G либо любая пара вершин смежна, т. е. G = K_n, либо любая пара вершин не смежна, т. е. G = O_n. В обоих случаях Aut G = S_nA_n.

Естественно возникает неизмеримо более сложный вариант вопроса Д. Кёнига. Этот, по-видимому, далекий от решения вариант известен как

Проблема Кёнига. Установить, какие условия необходимы и достаточны, чтобы для заданной на множестве V группы подстановок Г существовал такой граф G с множеством вершин V, что Aut G = Г.