
Физика (3 семестр) mobile
.pdf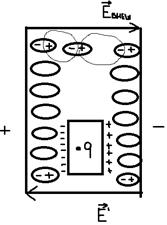
[ |
] |
Мы видим, что в однородном поле на диполь действует только пара сил, которая стремится повернуть диполь таким образом, чтобы вектор электрического момента был сонаправлен с вектором напряжённости внешнего электрического поля.
Воднородном электрическом поле диполь поворачивается вокруг своего центра масс вдоль силовых линий электрического поля и увеличивает расстояние между зарядами (если позволяет физика системы).
Внеоднородном электрическом поле диполь дополнительно притягивается в направлении градиента поля.
Вектор электрической индукции поля.
Внутренние электромагнитные процессы в веществе обычно настолько в среднем уравновешенны, что сами по себе не создают макроскопического поля. Исключение составляет лишь некоторые среды
(ферромагнетики). Под действием внешнего поля уравновешенность внутренних полей нарушается. Так например во внешнем электрическом поле происходит некоторая деформация и переориентация атомов и молекул, заряды которых остаются связанными (то есть
испытывают лишь некоторое отклонение от первоначального положения, что обеспечивает нейтральность каждого, мысленно выделяемого,
элементарного объёма |
). |
|
|
|
|
Если диэлектрик поместить во внешнее электрическое поле, создаваемое, например, между пластинами плоского конденсатора, то в результате отклонения связанных зарядов образуются диполи от первоначального положения, возникает внутреннее электрическое поле, которое заметно изменяет внешнее, наклоняясь на него. Под воздействием внешнего поля происходит поляризация диэлектрика:
диполи, образованные связанными зарядами, выстраиваются вдоль внешнего электрического поля.
Связанные заряды частично нейтрализуют свободные заряды на пластинах конденсатора, в результате напряжённость поля в диэлектрике оказывается меньше, чем в промежутке между пластинами в отсутствие диэлектрика.
Для того, чтобы изменить поле в диэлектрике, надо вырезать игольчатую полость, ориентированную вдоль внешнего электрического поля, и поместить туда пробный заряд q.

На концах полости связанные заряды будут очень малы и практически не будут влиять на напряжённость поля в диэлектрике:
̃
, где ̃– относительная электрическая проницаемость диэлектрика.
Сила, действующая на пробный заряд:
|
|
|
|
|
|
|
|
|
̃ |
||
|
|
||
, где |
– поле между пластинами конденсатора в |
||
вакууме.
Если в диэлектрике вырезать дискообразную полость, перпендикулярную внешнему электрическому полю, то сила, действующая на пробный заряд:
Таким образом, напряжённость поля в дискообразной полости совпадает с величиной внешнего поля.
Напряженность зависит от свойств среды, вектор напряжённости, переходящий через границу раздела диэлектриков, претерпевает скачкообразное изменение, создавая тем самым неудобства при расчёте полей.
Для удобства расчётов была введена ещё одна векторная характеристика электрического поля – вектор электрической индукции (смещения):
̃
̃
,где – электрическая постоянная.
̃
, где – абсолютная электрическая проницаемость диэлектрика.
Вектор напряженности описывает результирующее поле в диэлектрике, оно зависит от свойств диэлектрика.
Вектор электрической индукции описывает поле, создаваемое свободными зарядами.
Связанные заряды вызывают перераспределение свободных зарядов, следовательно, вектор электрической индукции характеризует поле, создаваемое свободными зарядами, но при таком их распределении, какое имеет место при наличии диэлектрика.
Силовые линии поля.
Линии, касающиеся в каждой точке векторов напряжённости и электрической индукции, называются силовыми линиями
электрического поля. В каждой точке силовой линии сила, действующая на пробный заряд, направлена по касательной к этой линии – отсюда следует их название «силовые».
Силовым линиям приписывают определённое направление, отмечая его на чертеже стрелкой.
Чтобы при помощи силовых линий изобразить не только направление, но и величину напряжённости поля, условились на графике поля проводить силовые линии с определённой густотой так, чтобы число силовых линий, проходящих через единичную поверхность перпендикулярно силовым линиям, было пропорционально величине напряжённости поля в данном месте.
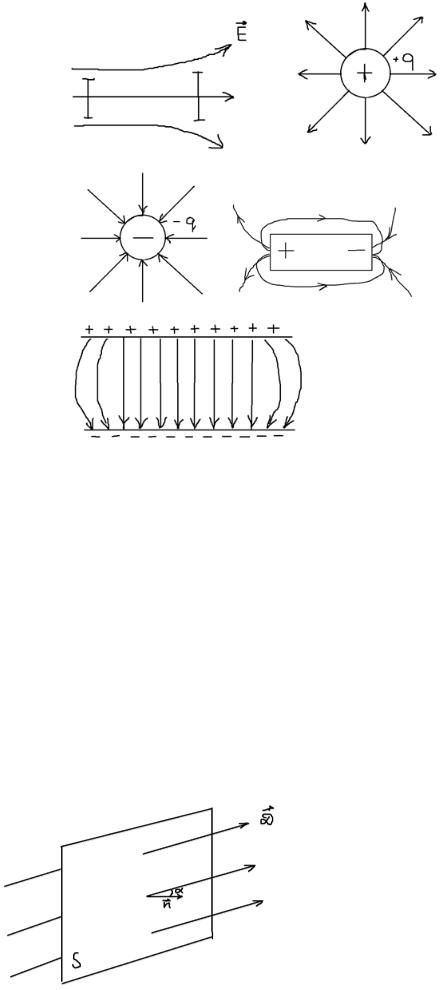
Силовые линии электрического поля начинаются на положительных и заканчиваются на отрицательных зарядах.
Обобщение закона Кулона. Теорема Гаусса.
Введём понятие потока вектора электрической индукции.
Рассмотрим в электрическом поле плоскую поверхность S и выберем направление нормали к этой поверхности.
Случай №1: будем полагать, что поле однородно и составляет произвольный угол с направлением нормали. Поток – величина, равная:
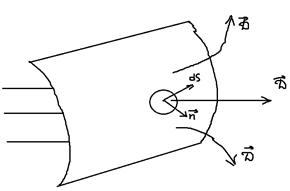
, где величина – поток вектора электрической индукции через поверхность S; – проекция вектора электрической индукции на направление нормали .
Так как густота линий электрической индукции равна модулю вектора электрической индукции, то можно сказать, что поток вектора электрической индукции через поверхность S равен полному числу линий электрического смещения, проходящему через эту поверхность.
Случай №2: поле неоднородно, поверхность, через которую протекает поток не является простой плоскостью. В таком случае поверхность можно разбить на бесконечно малые площадки , которые можно приближённо считать плоскими, а поле в предельной площадке можно считать однородным, тогда:
|
|
( ) |
|
|
|
|
∫ |
|
Пусть поле создано точечным зарядом q. Найдём поле точечного заряда в вакууме:

|
|
|
|
( ) |
|
|
|
|
|
||
, где |
- проекция площадки на плоскость, |
||||
перпендикулярную вектору электрического смещения;
- телесный угол (определение из Вики: часть
пространства, которая является объединением всех лучей, выходящих из данной точки (вершины угла) и пересекающих некоторую поверхность), под которым
видна площадка из точки, в которой находится заряд.
Пусть поверхность S будет замкнутой и заряд находится внутри поверхности. Для любой замкнутой поверхности
, вне зависимости от формы поверхности. Тогда, если поверхность замкнута и заряд распределён внутри неё, имеем:
|
|
|
|
|
|
|
|
, что является потоком через замкнутую поверхность.
Вывод: – поток вектора электрической индукции через замкнутую поверхность равен заряду этой поверхности.
Если поле создано суперпозицией полей нескольких точечных зарядов, то общий потенциал вектора электромагнитной индукции вычисляется как алгебраическая сумма отдельных потоков:
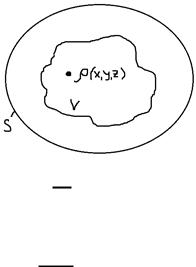
∑
Допустим, что плоскость имеет непрерывное распределение свободных зарядов с плотностью .
Тогда имеем:
Разбив объём на элементарные объёмы, каждый такой объём можно рассматривать как точечный заряд величиной:
Поток вектора электрической индукции, создаваемый зарядом через поверхность S будет вычисляться, как:
∫
, следовательно,
∫ ∑
Последняя формула выражает теорему Гаусса для вектора электрической индукции: поток вектора электрической индукции через замкнутую поверхность S равен суммарному свободному заряду, находящемуся внутри объёма, ограниченного этой поверхностью.
Эти уравнения – обобщение закона Кулона и называются теоремой Гаусса в интегральной форме.
Примеры решения задач с помощью теоремы Гаусса:
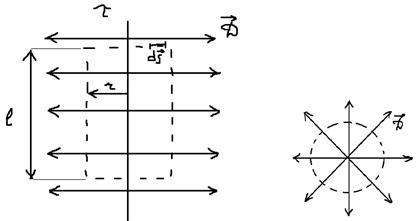
1. Найти поле бесконечной равномерно заряженной нити с линейной плотностью .
Электрическое поле зависит только от радиальных координат.
, где – мысленно выбираемая поверхность. Поскольку рассматриваем нить, то – цилиндр, система координат зависит от , где – угол, – радиус.
