
Физика (3 семестр) mobile
.pdf
Для ферромагнетиков линейная зависимость нарушается:
̃
При устремлении напряжённости магнитного поля в бесконечность, относительная магнитная проницаемость ферромагнетика стремится к единице.
Когда все молекулярные магнитные моменты ориентированы по полю, наступает насыщение, намагниченность дальше не увеличивается, а магнитная индукция, когда внешнее поле перестаёт изменяться, начинает линейно зависеть от напряжённости магнитного поля, то есть от внутреннего магнитного поля. Для ферромагнетиков характерны большие значения относительной магнитной проницаемости вещества и сложная зависимость относительной магнитной проницаемости вещества от напряжённости магнитного поля.
Характеристикой особых ферромагнетиков является магнитный гистерезис.
В следствие необратимости процесса намагничивания ферромагнетика при изменении внешнего магнитного поля от
до и обратно, зависимость вектора индукции от напряжённости магнитного поля изображается замкнутой кривой, называемой петлёй гистерезиса, где
– коэрцитивная сила (величина напряжённости магнитного поля, при которой индукция ферромагнетика уменьшается до нуля), (на рисунке – пересечение петель с осью ) – остаточная индукция, которая сохраняется в образце при нулевой напряжённости магнитного поля.
Площадь петли гистерезиса пропорциональна энергетическим затратам, затрачиваемым на один цикл перемагничивания. Эти потери вызывают нагрев образца:
|
|
|
|
Величины |
, |
и максимальная относительная |
|
магнитная проницаемость вещества ̃ |
являются |
||
основными характеристиками ферромагнетика.
Если коэрцитивная сила велика, то ферромагнетик называют жёстким, из таких ферромагнетиков изготавливают сильные магниты, если коэрцитивная сила мала – ферромагнетик называют мягким (например, сердечник трансформатора).
Из опытов по изучению магнитомеханических явлений следует, что ответственными за магнитные свойства ферромагнетиков являются собственные (спиновые) магнитные моменты электронов. Ферромагнетическими
свойствами могут обладать только кристаллические вещества, в атомах которых имеются недостроенные внешние оболочки с несколькими спинами.
При определённых условиях в кристалле возникают обменные силы, которые заставляют магнитные моменты электронов выстроиться параллельно друг другу, в результате возникают области спонтанного
(самопроизвольного) намагничивания - домены. Эти области намагничены до насыщения и обладают определённым магнитным моментом.
При отсутствии внешнего магнитного поля домены ориентированы хаотично и образец в целом не намагничен.
Действие внешнего поля на домены на разных стадиях намагничивания
оказывается различным. В начале наблюдается смещение границ доменов, в результате чего происходит увеличение тех доменов, магнитные моменты которых составляют меньший угол с направлением вектора напряжённости внешнего магнитного поля.
С увеличением напряжённости внешнего магнитного поля этот процесс идёт, пока домены с меньшим углом (обладающие в магнитном поле меньшей энергией, говорят, что эти домены расположены более выгодно) не поглотят целиком энергетически менее выгодные домены.
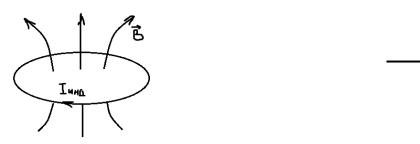
На следующей стадии имеет место поворот магнитных моментов этих доменов в направлении внешнего поля, при этом моменты электронов в пределах домена поворачиваются одновременно без нарушения их строгой параллельности друг другу.
Эти процессы являются необратимыми, что и служит причиной гистерезиса.
Для каждого ферромагнетика имеется определённая температура, при которой области спонтанной намагниченности распадаются и вещество утрачивает ферромагнитные свойства, такая температура называется точкой Кюри.
При температуре, большей чем точка Кюри, ферромагнетики становятся парамагнетиками.
Вихревое электрическое поле.
Рассмотрим неподвижный замкнутый проводник в магнитном поле.
Мы выяснили, что при всяком изменении магнитного поля,
пронизывающего площадку , в контуре возникает ЭДС индукции, под действием которой начинает протекать индукционный ток.
С другой стороны известно, что ЭДС в любой цепи возникает только в том случае, если на заряды действуют какие-либо сторонние силы, т.е. силы не электростатического происхождения.
Какова природа сторонних сил в опыте?
Опыт показывает, что ЭДС индукции совершенно не зависит от рода вещества проводника или от его состояния (например, температуры). Это указывает на то, что сторонние силы не связаны с изменением свойств проводника в магнитном поле, а обусловлены самим магнитным полем.
Анализируя явления электромагнитной индукции, Максвелл заключил, что причиной ЭДС индукции является возникновение электрического поля в пространстве, а проводник играет второстепенную роль и является своего рода прибором, обнаруживающим это поле.
Под действием поля электрические проводимости в проволоке приходят в движение и, если проволока замкнута, в ней возникает индукционный ток.
Существенная особенность рассматриваемого явления заключается в том, что возникшее электрическое поле не является электростатическим, силовые линии электростатического поля всегда разомкнуты (начинаются и заканчиваются на электрических зарядах), в соответствии с
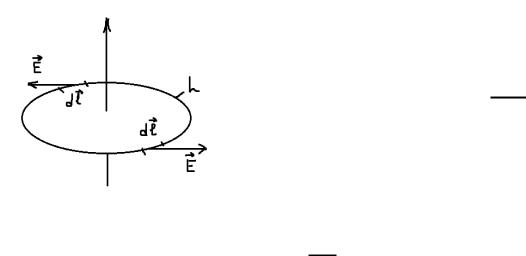
чем напряжение в электростатическом поле по замкнутому контуру всегда равно нулю.
По этой причине электростатическое поле не может поддерживать замкнутое движение зарядов. Напротив,
электрическое поле, возникающее при электромагнитной индукции, имеет непрерывные силовые линии, т.е. представляет собой вихревое поле. Это поле вызывает в проводнике движение электронов по замкнутой траектории и сторонними силами являются силы вихревого электрического поля.
Таким образом, углубленное истолкование метода электромагнитной индукции приводит к следующему выводу, выражает первое основное положение теории Максвелла:
Всякое изменение магнитного поля вызывает появление вихревого электрического поля.
Полученный результат можно выразить в количественной форме:
∫
∫
|
|
|
|
|
|
∫ |
(1) |
|
|||
Уравнение (1) - обобщение закона электромагнитной индукции.
Здесь – напряженность поля сторонних сил. В данном случае – напряженность вихревого электрического поля.
Циркуляция вектора напряженности электрического поля по замкнутому контуру L равна скорости изменения потока вектора магнитной индукции, пронизывающего площадку S, опирающуюся на данный контур L, взятый с обратным знаком (знак “-“ так же определяется правилом Ленца).
Ток смещения.
Выше мы установили, что любое переменное магнитное поле вызывает появление вихревого электрического поля. Анализируя различные электромагнитные процессы, Максвелл пришел к заключению, что должно существовать и обратное явление: всякое изменение электрического поля вызывает появление вихревого поля.
Это утверждение выражает второе основное положение теории Максвелла.
Максвелл взял плоский конденсатор, зарядил его, и стал исследовать наличие магнитного поля, возникающего пи
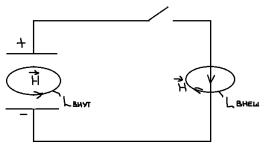
замыкании внешней цепи, как снаружи конденсатора, так и между его пластинами.
При замыкании внешней цепи конденсатор начинает разряжаться и во внешней цепи протекает ток , вокруг возникает вихревое магнитное поле, для которого:
, где |
– контур во внешней области. |
Исследуя поле между пластинами конденсатора, Максвелл обнаружил, что несмотря на отсутствие в этой области токов проводимости, в ней существует магнитное поле, силовые линии являются замкнутыми в пределах конденсатора.
При этом направление магнитного поля таково, как будто оно создается током, протекающим в направлении от нижней пластины к верхней.
Согласно Максвеллу, электрическое поле в конденсаторе в любой момент времени создает такое же магнитное поле, как если бы между обкладками существовал ток проводимости силой, равной силе тока в металлическом проводнике.

Магнитное поле разомкнутого контура оказывается таким же, как если бы контур был замкнут.
Под действием переменного электрического поля, существующего между обкладками конденсатора, возникает вихревое магнитное поле, а так как есть обязательный признак всякого тока, то Максвелл назвал переменное электрическое поле током смещения.
Можно найти количественную связь между меняющимся электрическим полем и, вызываемым им, магнитным полем:
, где – поверхностная плотность заряда на обкладках.
Полный заряд каждой обкладки:
, где – площадь обкладки.
Тогда сила тока:
, где |
– плотность тока смещения. |
Количественные исследования показали, что:
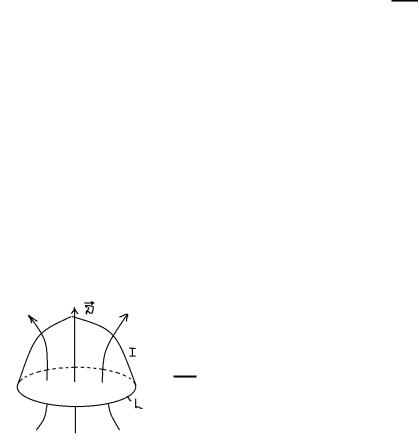
|
|
∫ |
|
, где – контур в пространстве между пластинами конденсатора; – площадка, опирающаяся на этот контур.
Величина, равная
∫
была названа Максвеллом током смещения.
Если через площадку контура наряду с изменяющимся во времени электрическим полем проходит ещё и ток проводимости, то уравнения можно объединить:
|
|
∫ |
|
Это уравнение, обобщающее сведения об источниках вихревого магнитного поля.
Магнитное поле создается двумя видами токов: током проводимости и током смещения.
Рассмотрим направление векторов в плоскости и токов в проводимости и смещения.
