
Физика (3 семестр) mobile
.pdf
Токи Фуко, как и индукционные токи в линейных проводниках, подчиняются правилу Ленца: магнитное поле этих токов направлено так, чтобы препятствовать внешнему магнитному полю, вызвавшему это поле.
Маятник в виде массивного металлического диска совершает колебания около электромагнита.
Когда электромагнит выключен, маятник совершает колебания с очень мелкими затуханиями. Когда электромагнит включен, то переменное (из-за колебаний маятника) магнитное поле создаёт в маятнике вихревые токи, направление которых таково, что магнитное поле вихревых токов препятствует изменению внешнего магнитного поля, что приводит к остановке маятника.
Вихревые токи вызывают нагревание проводника,
поэтому для уменьшения потерь на нагрев якоря генераторов и электродвигателей делают не сплошными, а набирают из отдельных пластин, отделённых изолирующими слоями, при этом пластины устанавливаются так, чтобы вихревые токи были перпендикулярно им.
Полезную роль токи Фуко играют в индукционной печи. Она представляет собой большую катушку индуктивности, внутрь которой помещают металл для расплавки и тигель (форму).
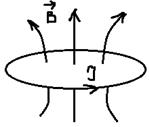
Явление самоиндукции.
Возьмём замкнутый контур и будем создавать в нём ток.
∫
При изменении тока изменится поток магнитного поля, пронизывающего площадку контура, вследствие чего в контуре индуцируется ЭДС – самоиндукция.
Поскольку в соответствии с законом Био-Савара вектор индуктивности пропорционален силе тока, то и поток магнитного поля пропорционален силе тока:
, где – коэффициент пропорциональности (индуктивность контура).
Линейная зависимость наблюдается только в том случае, когда магнитная проницаемость среды не зависит от направления магнитного потока, то есть, в отсутствие ферромагнетиков.
При постоянной силе тока поток может меняться за счёт изменения формы и размеров контура. Из сказанного следует, что индуктивность контура зависит от геометрии контура, а также от магнитных свойств окружающей контур среды.

Вычислим индуктивность соленоида длиной , содержащего витков, площадью каждый.
Пусть внешнее поле – однородное, тогда:
Если вблизи контура нет ферромагнетиков, то ЭДС самоиндукции равна:
Знак минус обусловлен правилом Ленца, согласно которому индукционный ток направлен так, чтобы препятствовать причине, его вызывающей.
Когда (при возрастании тока) - ,
индукционный ток направлен навстречу току в контуре;
когда (при убывании тока) - , индукционный
ток сонаправлен с током в контуре.
За единицу индукции в СИ принята индуктивность такого проводника, у которого при силе тока в один ампер возникает сцепление с ним полного потока магнитного поля, величиной один вебер:
[ ]
В присутствие ферромагнетиков индуктивность будет функцией от силы тока через напряжённость магнитного поля, и при этом ЭДС самоиндукции равна:
( |
|
|
|
) [ |
|
|
|
|
|
] |
|
|
|
|
|
( )
Взаимная индукция.
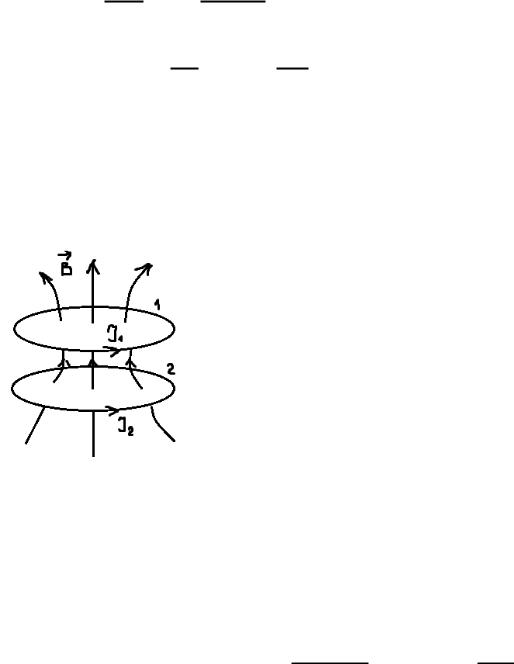
Возьмём два проводящих контура, расположенных близко друг к другу.
В каждом контуре протекает ток, каждый контур создаёт свой магнитный поток.
Частично магнитный поток верхнего контура пронизывает площадку нижнего и наоборот.
Предположим, что есть только . Изменим его – во втором контуре возникнет ЭДС самоиндукции – ЭДС взаимной индукции:
, где – та часть магнитного потока, создаваемого первым контуром, которая пронизывает второй контур.
Если есть только , то:
, где – та часть магнитного потока, создаваемого вторым контуром, которая пронизывает первый контур.
Есть коэффициент взаимной индукции. Они зависят от геометрии формы, размеров и взаимного расположения контуров. Контуры 1 и 2 называются связанными.
Если изменить направление сил токов, то изменится и направление ЭДС, которое определяется правилом Ленца.
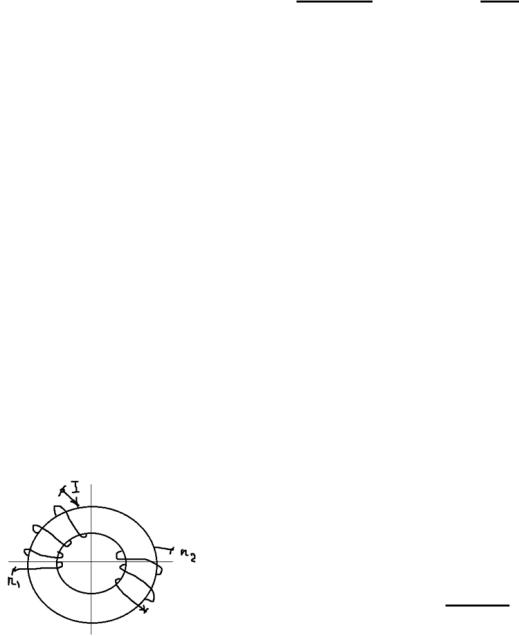
Вычислим взаимную индуктивность двух катушек, намотанных на общий тороидальный сердечник:
,где – длина средней линии тороида.
,где – поток магнитного поля через вторую обмотку.
Поскольку магнитный поток создаётся первым током, то можно записать, что:

Трансформаторы.
Сердечник делают из металла, потому что магнитное поле как бы втягивается внутрь сердечника и не рассеивается вокруг.
Затем для первичной обмотки уравнение по правилу Кирхгофа:
,где – поток, пронизывающий один виток.
,следовательно:
,следовательно:
,где знак минус говорит о том, ЭДС обмоток изменяются в противофазе.
, где |
|
– коэффициент трансформации, если |
, то |
|
|
||||
трансформатор понижающий, если |
– повышающий. |
|||
Энергия магнитного поля тока.
Проводник, по которому протекает электрический ток, всегда окружён магнитным полем. Энергия магнитного поля
равна работе, выполняемой током по созданию этого магнитного поля.
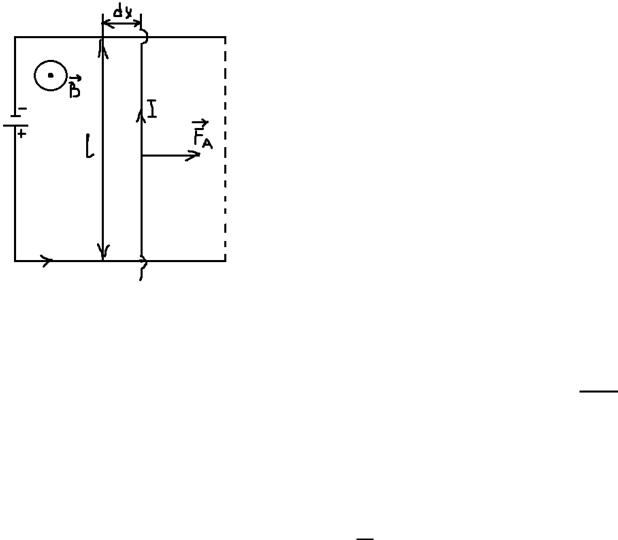
Рассмотрим контур, находящийся в однородном магнитном поле:
Подвижная перемычка перемещается на расстояние за время под действием силы Ампера:
C другой стороны:
∫
Энергия магнитного поля, связанного с контуром:
Магнитное поле локализовано в пространстве. Энергию магнитного поля можно выразить через величины, характеризующие само поле:
∫
̃
̃
, где – объёмная плотность энергии магнитного поля.
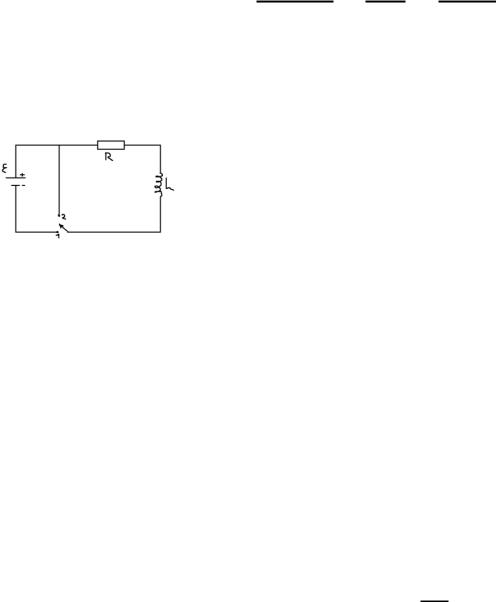
Процессы при замыкании и размыкании LR-цепи.
При всяком изменении тока в проводящем контуре, в нём возникает ЭДС самоиндукции, в результате чего в контуре
появляются экстратоки самоиндукции.
Согласно правилу Ленца они всегда направлены так, чтобы препятствовать току в цепи (препятствовать возникновению тока при замыкании цепи и исчезанию тока при размыкании цепи).
Поставим переключатель в положение 1 и запишем для цепи второе правило Кирхгофа:
Обозначим |
, тогда: |
Из формулы (2) выразим силу тока:
Подставим (4) в (3):
Разделим переменные:
Возьмём неопределённый интеграл:
∫∫
Постоянная интегрирования находится из начальных условий.
При = 0 сила тока в цепи равна нулю, из формулы (2) имеем:
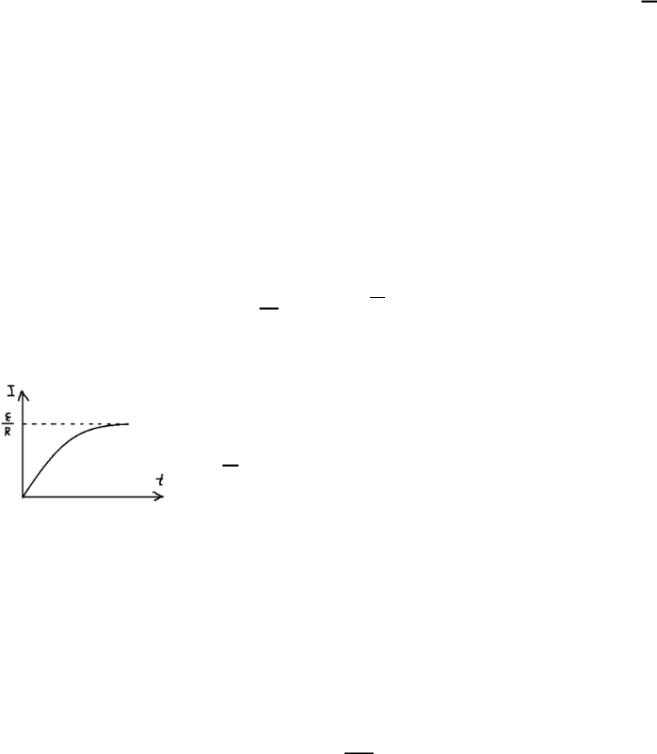
Подставляем, находим постоянную интегрирования:
|
|
[ |
] |
|
|
|
|
||
|
|||||||||
Заменим постоянную интегрирования и вернёмся к |
|||||||||
формуле (2), заменив |
: |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( )
Формула (6) – закон нарастания тока в цепи с индуктивностью.
– время релаксации – время, в
течение которого сила тока уменьшится
в е раз.
Поставим переключатель в положение 2, отключив внешний источник ЭДС, оставляя только ЭДС самоиндукции.
Составим уравнение по второму правилу Кирхгофа:
Разделим переменные:
