
2003_denisov / сборник / ГЛ. 9
.docГЛАВА 9
КАНОНИЧЕСКИЙ ВИД ЛИНЕЙНЫХ ОПЕРАТОРОВ
§ 9.1. ЖОРДАНОВА НОРМАЛЬНАЯ ФОРМА МАТРИЦ
Известно, что матрица оператора простой структуры приводится к диагональному виду. В общем случае комплексная квадратная матрица приводится к квазидиагональной, так называемой жордановой форме.
Пусть линейный оператор А, действующий в n-мерном комплексном пространстве X, в некотором базисе этого пространства имеет матрицу А, характеристический многочлен которой представлен в виде канонического разложения
![]()
![]()
![]() ,
(9.1.1)
,
(9.1.1)
где
![]() – попарно различные собственные
значения,
– попарно различные собственные
значения,
![]() – соответствующие им алгебраические
кратности и
– соответствующие им алгебраические
кратности и
![]() .
.
Корневым
подпространством
![]() оператора А,
отвечающим собственному значению
оператора А,
отвечающим собственному значению
![]() с алгебраической кратностью
с алгебраической кратностью
![]() ,
называется ядро оператора
,
называется ядро оператора
![]() ,
т.е.
,
т.е.
![]() .
(9.1.2)
.
(9.1.2)
Векторы корневых подпространств называются корневыми векторами.
Размерность
корневого подпространства
![]() равна
равна
![]() .
Каждое корневое подпространство
.
Каждое корневое подпространство
![]() инвариантно относительно оператора А,
и пространство X
разлагается в прямую сумму корневых
подпространств
инвариантно относительно оператора А,
и пространство X
разлагается в прямую сумму корневых
подпространств
![]() .
(9.1.3)
.
(9.1.3)
Базис пространства
X,
составленный как последовательное
объединение базисов всех корневых
подпространств
![]() ,
называется корневым
базисом.
,
называется корневым
базисом.
Пусть
![]() – одно из корневых подпространств.
Тогда в нем существуют собственный
вектор
– одно из корневых подпространств.
Тогда в нем существуют собственный
вектор
![]() и векторы
и векторы
![]() ,
удовлетворяющие условиям
,
удовлетворяющие условиям
![]() ,
,
![]() ,
,
![]() ,
(9.1.4)
,
(9.1.4)
. . . . . . . . .
![]() .
.
Векторы
![]() называются присоединенными
к
называются присоединенными
к
![]() векторами первого, второго и более
высоких порядков.
Вместе с вектором
векторами первого, второго и более
высоких порядков.
Вместе с вектором
![]() они образуют в
они образуют в
![]() жорданову
цепочку длиной h
с началом в
жорданову
цепочку длиной h
с началом в
![]() .
Линейная оболочка
.
Линейная оболочка
![]() корневых векторов
корневых векторов
![]() образует h-мерное
циклическое
подпространство,
порожденное собственным вектором
образует h-мерное
циклическое
подпространство,
порожденное собственным вектором
![]() .
.
Корневое
подпространство
![]() распадается в прямую сумму
распадается в прямую сумму
![]()
![]()
![]() инвариантных относительно оператора
А
циклических подпространств.
инвариантных относительно оператора
А
циклических подпространств.
Корневой базис, составленный как последовательное объединение базисов циклических подпространств, называется корневым базисом Жордана (жордановым базисом).
Клеткой Жордана
![]() называется верхняя треугольная матрица
размером kk,
имеющая вид
называется верхняя треугольная матрица
размером kk,
имеющая вид
 .
(9.1.5)
.
(9.1.5)
По определению
![]() .
.
В жордановом базисе
матрица оператора А
имеет жорданову
нормальную форму,
т.е. является квазидиагональной матрицей
J,
состоящей из жордановых клеток,
расположенных по главной диагонали.
Первыми располагаются жордановы клетки,
соответствующие собственному значению
![]() ,
затем жордановы клетки, соответствующие
собственному значению
,
затем жордановы клетки, соответствующие
собственному значению
![]() и т.д. При этом жордановы клетки
располагаются в матрице J
по главной диагонали в том же порядке,
в каком расположены в жордановом базисе
соответствующие им жордановы цепочки.
и т.д. При этом жордановы клетки
располагаются в матрице J
по главной диагонали в том же порядке,
в каком расположены в жордановом базисе
соответствующие им жордановы цепочки.
Таким образом, матрица J имеет вид



![]()

![]()
J
=
![]() . (9.1.6)
. (9.1.6)

![]()

![]()
В жордановой
матрице J
по каждому
![]() жордановы клетки располагаются по
убыванию их порядков. Некоторые из
жордановых клеток могут повторяться,
а некоторые из жордановых клеток низших
порядков могут отсутствовать. Частным
случаем жордановой матрицы является
диагональная матрица.
жордановы клетки располагаются по
убыванию их порядков. Некоторые из
жордановых клеток могут повторяться,
а некоторые из жордановых клеток низших
порядков могут отсутствовать. Частным
случаем жордановой матрицы является
диагональная матрица.
Заметим, что если в построенном жордановом базисе изменить нумерацию жордановых цепочек, то в жордановой матрице на главной диагонали соответственно изменятся положения жордановых клеток.
Всякая комплексная матрица А подобна жордановой матрице J, которая определена с точностью до порядка расположения клеток Жордана на главной диагонали:
![]() АР,
(9.1.7)
АР,
(9.1.7)
где Р – матрица перехода от исходного базиса пространства X к его жорданову базису.
Матрица Р состоит из столбцов координат векторов жорданова базиса в исходном базисе. Причем эти столбцы располагаются в матрице Р в том же порядке, в каком располагаются соответствующие им векторы в жордановом базисе пространства X. Матрица Р называется трансформирующей, или приводящей, матрицу А к ее жордановой форме J.
Пример.
Постройте жорданов базис оператора с
матрицей
 ,
жорданову форму J
этой матрицы
и трансформирующую матрицу Р.
,
жорданову форму J
этой матрицы
и трансформирующую матрицу Р.
Решение. В настоящее время в учебной литературе по линейной алгебре описано достаточно много способов решения задач данного типа (см., например, [3, 10, 14, 15, 18]). Воспользуемся одним из двух подходов, указанных в книге [3].
Начнем с нахождения собственных значений матрицы А. Поскольку
 ,
,
матрица А
имеет только одно собственное значение
![]() .
Его алгебраическая кратность
.
Его алгебраическая кратность
![]() .
.
Выясним, какова
геометрическая кратность
![]() .
.
 .
(9.1.8)
.
(9.1.8)
Геометрическая
кратность собственного значения
![]() равна
равна
![]() .
.
Поскольку
геометрическая кратность
![]() меньше алгебраической, матрица А
не является матрицей простой структуры
(А
– дефектная
матрица).
меньше алгебраической, матрица А
не является матрицей простой структуры
(А
– дефектная
матрица).
В силу того, что А
имеет только одно собственное значение,
трехмерное пространство X,
в котором действует линейный оператор,
совпадает с корневым подпространством
![]() .
Это подпространство разложимо в прямую
сумму двух циклических подпространств
размерности 2 и 1. Таким образом, искомый
жорданов базис состоит из двух собственных
векторов и одного присоединенного
вектора первого порядка.
.
Это подпространство разложимо в прямую
сумму двух циклических подпространств
размерности 2 и 1. Таким образом, искомый
жорданов базис состоит из двух собственных
векторов и одного присоединенного
вектора первого порядка.
Определим
общий вид собственных векторов
![]() ,
для чего решим однородную систему
уравнений
,
для чего решим однородную систему
уравнений
![]() .
Из (9.1.8) видно, что в качестве свободных
переменных можно выбрать
.
Из (9.1.8) видно, что в качестве свободных
переменных можно выбрать
![]() и
и
![]() .
Тогда
.
Тогда
![]() и
и
![]() .
(9.1.9)
.
(9.1.9)
Для построения
жорданова базиса осталось найти
присоединенный вектор первого порядка
![]() .
Решим неоднородную систему уравнений
.
Решим неоднородную систему уравнений
![]() :
:
 .
(9.1.10)
.
(9.1.10)
В соответствии с
теоремой Кронекера – Капели система
(9.1.10) совместна тогда и только тогда,
когда
![]() .
Подставляя это условие в выражение
(9.1.9), получаем общий вид собственных
векторов, имеющих присоединенные векторы
первого порядка:
.
Подставляя это условие в выражение
(9.1.9), получаем общий вид собственных
векторов, имеющих присоединенные векторы
первого порядка:
![]() .
Найдем общий вид присоединенных векторов
в зависимости от значения
.
Найдем общий вид присоединенных векторов
в зависимости от значения
![]() ,
для чего продолжим решение системы
(9.1.10)
,
для чего продолжим решение системы
(9.1.10)
 .
.
Выбирая в качестве
свободных переменных
![]() и
и
![]() ,
получаем, что
,
получаем, что
![]() и
и
![]() .
.
Полагая значения
свободных переменных
![]() ,
,
![]() ,
,
![]() ,
найдем собственный вектор
,
найдем собственный вектор
![]() и присоединенный к нему вектор первого
порядка
и присоединенный к нему вектор первого
порядка
![]() .
Оставшийся вектор жорданова базиса
определим, выбирая в выражении (9.1.9)
.
Оставшийся вектор жорданова базиса
определим, выбирая в выражении (9.1.9)
![]() и
и
![]() .
Получим вектор
.
Получим вектор
![]() .
Векторы
.
Векторы
![]() образуют искомый жорданов базис, в
котором матрица линейного оператора
имеет вид
образуют искомый жорданов базис, в
котором матрица линейного оператора
имеет вид
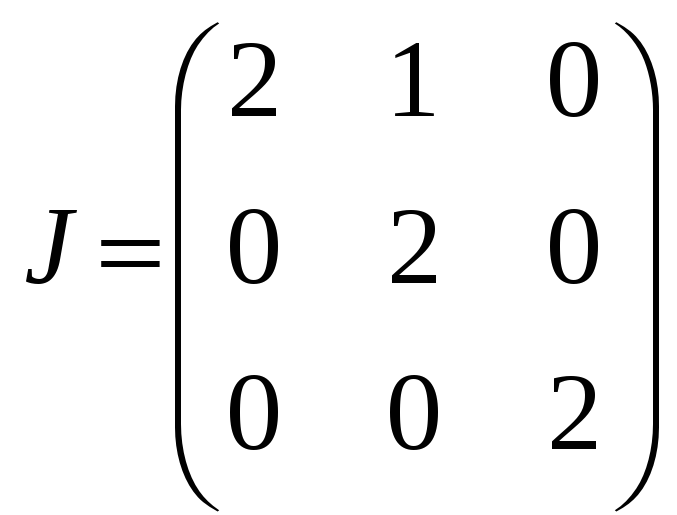 .
.
Запишем трансформирующую матрицу:

и проверим правильность полученных результатов:

9.1.1. Постройте жорданов базис оператора с матрицей А, жорданову форму J матрицы А и трансформирующую матрицу Р для следующих матриц А:
а)
 ;
в)
;
в)
 ;
;
б)
 ;
г)
;
г)
 ;
;
д)
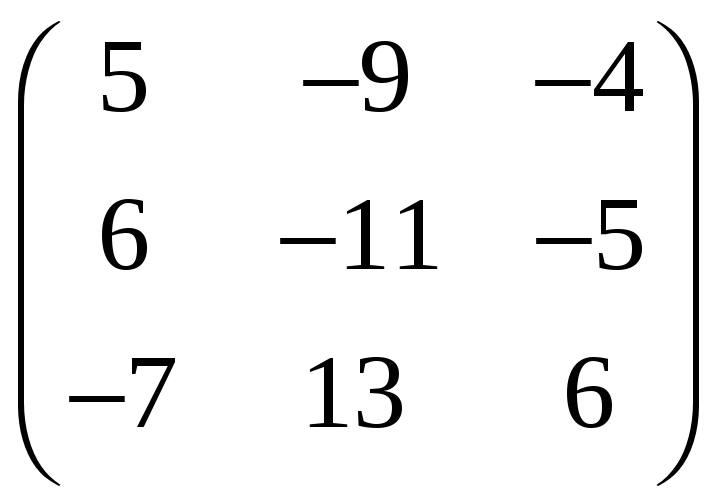 ;
л)
;
л)
 ;
;
е)
 ; м)
; м)
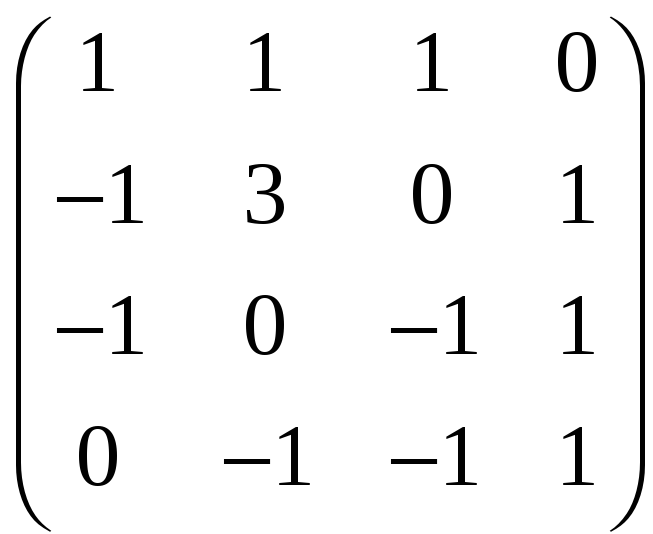 ;
;
ж)
 ;
н)
;
н) ;
;
з)
 ;
о)
;
о)
 ;
;
и)
 ; п)
; п)
 .
.
к)
 ;
;
9.1.2.
Найдите квадрат жордановой клетки
![]() .
.
9.1.3.
Найдите жорданову форму квадрата
жордановой клетки
![]() при
при
![]() .
.
9.1.4.
Найдите жорданову форму квадрата
жордановой клетки
![]() ,
если
,
если
а) k = 4;
б) k = 5.
9.1.5. Постройте корневое подпространство для следующих матриц:
а)
 ;
;
б)
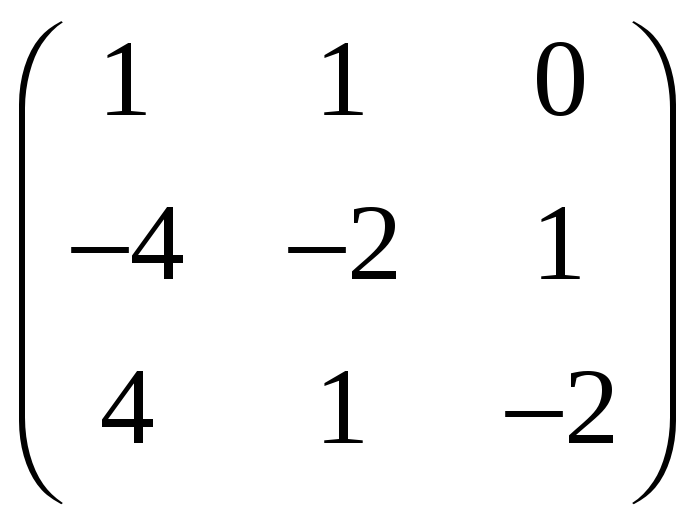 .
.
9.1.6.
Найдите канонический базис и жорданову
форму оператора дифференцирования в
пространстве
![]() .
.
9.1.7.
В пространстве многочленов
![]() найдите жорданову форму оператора
найдите жорданову форму оператора
![]() .
.
§ 9.2. λ – МАТРИЦЫ
Квадратная матрица, элементами которой являются многочлены от λ, называется λ-матрицей (полиномиальной матрицей). Степенью λ-матрицы называется максимальная из степеней многочленов, образующих элементы матрицы.
Элементарными преобразованиями λ-матриц называются преобразования следующих типов:
1) перестановка между собой двух каких-либо строк или столбцов матрицы;
2) прибавление к строке какой-либо другой строки, умноженной на некоторый многочлен φ(λ), и аналогично прибавление к столбцу другого столбца, умноженного на некоторый многочлен;
3) умножение строки или столбца на некоторое число, отличное от нуля.
Две λ-матрицы А(λ) и В(λ) называются эквивалентными, если одна может быть получена из другой при помощи конечного числа элементарных преобразований. Эквивалентность λ-матриц записывается следующим образом: А(λ) – В(λ).
Всякая λ-матрица может быть элементарными преобразованиями приведена к виду
 ,
(9.2.1)
,
(9.2.1)
где многочлены
![]() ,
стоящие по диагонали, имеют старшие
коэффициенты, равные единице, многочлен
,
стоящие по диагонали, имеют старшие
коэффициенты, равные единице, многочлен
![]() делится на
делится на
![]() ,
,
![]() делится на
делится на
![]() и т.д. Этот вид называется нормальной
диагональной формой λ-матрицы,
а многочлены
и т.д. Этот вид называется нормальной
диагональной формой λ-матрицы,
а многочлены
![]() – инвариантными
множителями.
– инвариантными
множителями.
Нормальная
диагональная форма λ-матрицы А(λ)
определяется по ней однозначно. Если
![]() – наибольший общий делитель миноров
k-порядка
матрицы А(λ),
а
– наибольший общий делитель миноров
k-порядка
матрицы А(λ),
а
![]()
![]() ,
то элементы нормальной диагональной
формы (9.2.1) определяются по формулам
,
то элементы нормальной диагональной
формы (9.2.1) определяются по формулам
![]() ,
,
![]() ,
,
.......... (9.2.2)
![]() ,
,
![]() .
.
Таким образом, система инвариантных множителей λ-мат-рицы может быть получена с помощью либо элементарных преобразований, либо наибольших общих делителей ее миноров.
Для того чтобы две λ-матрицы А(λ) и В(λ) были эквивалентны, необходимо и достаточно, чтобы они имели одни и те же инвариантные множители.
Числовые матрицы
А
и В
одного порядка подобны
![]() тогда и только тогда, когда инвариантные
множители λ-матриц
тогда и только тогда, когда инвариантные
множители λ-матриц
![]() и
и
![]() совпадают между собой (критерий
подобия матриц).
совпадают между собой (критерий
подобия матриц).
Пусть матрица А
имеет жорданову нормальную форму J,
в которой имеется p
клеток порядков
![]()
![]() ,
отвечающих собственному значению
,
отвечающих собственному значению
![]() ,
q
клеток порядков
,
q
клеток порядков
![]()
![]() ,
отвечающих собственному значению
,
отвечающих собственному значению
![]() ,
и т. д.; тогда инвариантные множители
,
и т. д.; тогда инвариантные множители
![]() матрицы
матрицы
![]() имеют вид
имеют вид
![]() ,
,
![]() ,
,
![]() ,
,
..................
Таким образом,
задание последовательности инвариантных
множителей
![]() полностью определяет жорданову нормальную
форму матрицы А;
собственные значения
полностью определяет жорданову нормальную
форму матрицы А;
собственные значения
![]() получаются как корни уравнения
получаются как корни уравнения
![]() .
Размеры же
.
Размеры же
![]() клеток, отвечающих данному собственному
значению
клеток, отвечающих данному собственному
значению
![]() ,
равны степеням, с которыми
,
равны степеням, с которыми
![]() содержится соответственно в
содержится соответственно в
![]()
Матрица А
имеет простую структуру тогда и только
тогда, когда все инвариантные множители
λ-матрицы
![]() имеют только простые корни.
имеют только простые корни.
Скалярный многочлен
φ(λ) называется аннулирующим
многочленом
квадратной матрицы А,
если φ![]() .
В частности, одним из аннулирующих
многочленов матрицы является ее
характеристический многочлен. Многочлен
наименьшей степени среди ненулевых
аннулирующих многочленов матрицы А
со старшим коэффициентом 1 называется
минимальным
многочленом
матрицы А.
Любой аннулирующий многочлен матрицы
делится на ее минимальный многочлен.
.
В частности, одним из аннулирующих
многочленов матрицы является ее
характеристический многочлен. Многочлен
наименьшей степени среди ненулевых
аннулирующих многочленов матрицы А
со старшим коэффициентом 1 называется
минимальным
многочленом
матрицы А.
Любой аннулирующий многочлен матрицы
делится на ее минимальный многочлен.
Минимальный
многочлен ψ(λ) матрицы А
равен последнему инвариантному множителю
![]() λ-матрицы
λ-матрицы
![]() .
.
Пример 1. При помощи инвариантных множителей найдите жорданову нормальную форму матрицы
 .
.
Укажите минимальный многочлен этой матрицы.
Решение.
Запишем λ-матрицу
![]() и,
воспользовавшись методикой, подробно
изложенной в книге [6, § 22], приведем ее
к нормальной диагональной форме:
и,
воспользовавшись методикой, подробно
изложенной в книге [6, § 22], приведем ее
к нормальной диагональной форме:
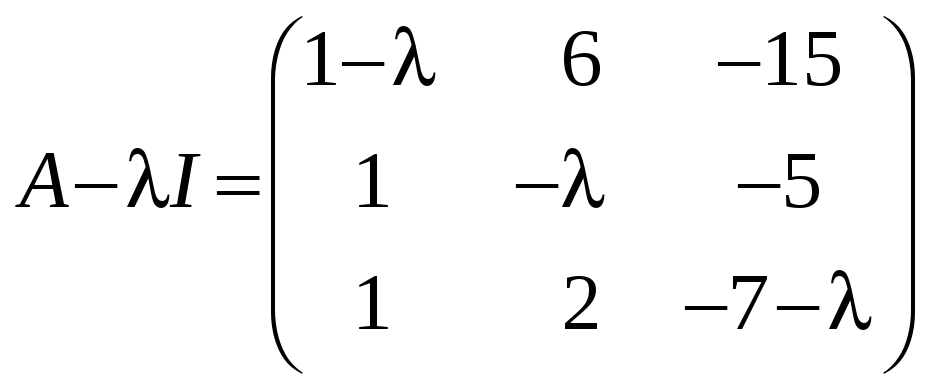 .
.
Поменяем местами первую и вторую строки:
 .
.
Теперь, прибавляя ко второму и третьему столбцам первый, предварительно умноженный соответственно на λ, 5, получаем
 .
.
Прибавляя ко второй
и третьей строкам первую, предварительно
умноженную соответственно на
![]() ,
–1, получаем
,
–1, получаем
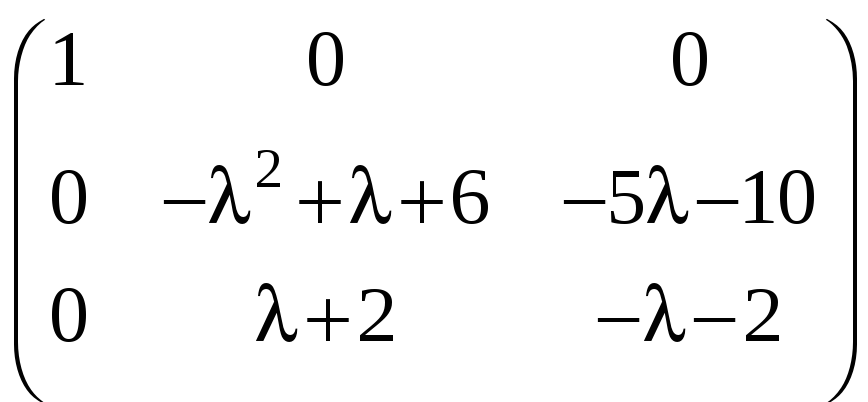 .
.
Поменяем местами вторую и третью строки:
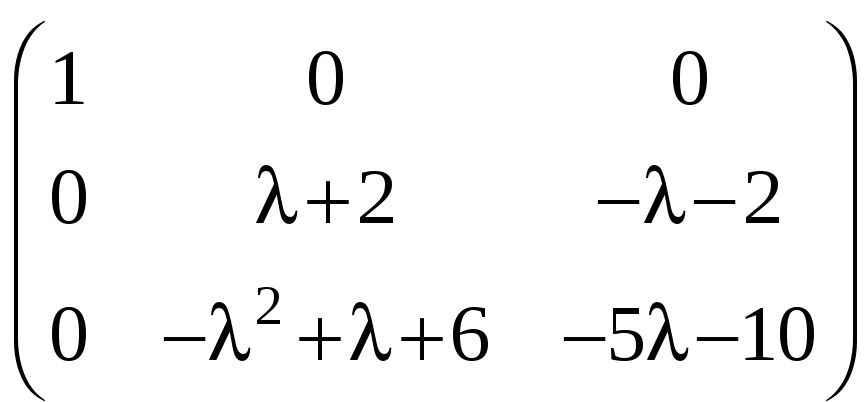 .
.
Прибавляя к третьему столбцу второй, находим:
 .
.
Прибавляя к третьей
строке вторую, умноженную на
![]() ,
получаем:
,
получаем:
 .
.
Умножая третий
столбец на (–1), приходим к нормальной
диагональной форме λ-матрицы
![]() :
:
 ,
,
инвариантные
множители которой
![]() ,
,
![]() ,
,
![]() позволяют составить жорданову нормальную
форму
позволяют составить жорданову нормальную
форму

и минимальный
многочлен
![]() .
.
Пример 2. Выясните, подобны ли между собой матрица А из примера 1 и матрица
 .
.
Решение.
Найдем инвариантные множители λ-матрицы
![]() ,
для чего приведем ее к нормальной
диагональной форме.
,
для чего приведем ее к нормальной
диагональной форме.
 .
.
Умножим второй
столбец на
![]() и поменяем местами его с первым столбцом:
и поменяем местами его с первым столбцом:

Прибавляя ко
второму и третьему столбцам первый,
предварительно умноженный на
![]() ,
15, получаем:
,
15, получаем:
 .
.
Теперь, прибавляя
ко второй и третьей строкам первую,
предварительно умноженную на
![]() ,
,
![]() ,
находим:
,
находим:
 .
.
Третий столбец умножим на (–1) и поменяем местами со вторым столбцом. Будем иметь:
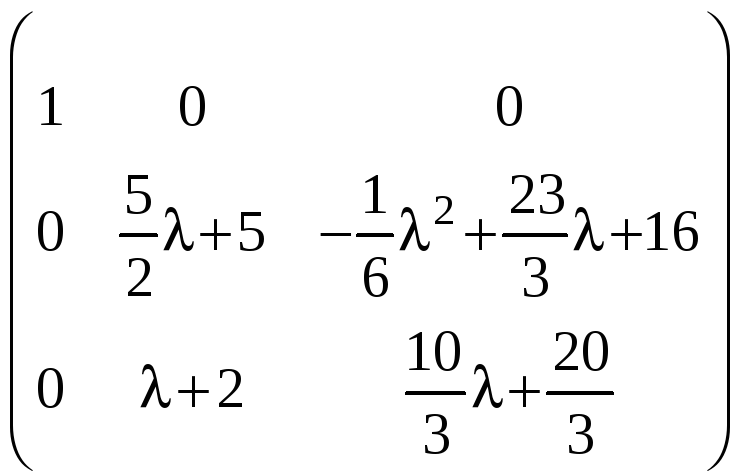 .
.
Поменяем местами вторую и третью строки:
 .
.
Прибавляя к третьему
столбцу второй, предварительно умноженный
на
![]() ,
получаем:
,
получаем:
 .
.
Прибавляя к третьей
строке вторую, предварительно умноженную
на
![]() ,
находим:
,
находим:
 .
.
Умножая третий
столбец на (–6), приходим к нормальной
диагональной форме λ-матрицы
![]() :
:
 .
.
Выпишем
инвариантные множители этой матрицы:
![]() ,
,
![]() ,
,
![]() .
Поскольку инвариантные множители
λ-матриц
.
Поскольку инвариантные множители
λ-матриц
![]() и
и
![]() между собой совпадают, согласно критерию
подобия матриц матрицы А
и В
подобны.
между собой совпадают, согласно критерию
подобия матриц матрицы А
и В
подобны.
9.2.1. Путем элементарных преобразований приведите следующие λ-матрицы к нормальной диагональной форме:
а)
![]() ;
;
б)
![]() ;
;
в)
 ;
;
г)
 ;
;
