Заряд в магнитном поле

Магнитное поле наряду с электрическим полем широко используется для изменения и контроля состояния электрона. Магнитное поле влияет на фазу волновой функции заряда и на длину волны де Бройля. Это используется для измерения эффективной массы и магнитного момента носителя тока в кристалле, для определения поверхности Ферми и концентрации электронного газа.

Длина волны де Бройля

определяется в магнитном поле не кинетическим импульсом частицы , а полным импульсом.

Полный импульс P учитывает влияние магнитного поля на волновую функцию заряда. Пусть магнитное поле создано электрическим полем благодаря явлению электромагнитной индукции, описываемому уравнением Максвелла

,

где А – векторный потенциал, через который выражается индукция магнитного поля

.

Получаем

.

Учитываем

,

где  – произвольная скалярная функция, тогда

.

Векторный потенциал в классической электродинамике не измерим, его выбор не однозначен. Используем калибровку

,

получаем , в результате

.

Векторный потенциал создает вихревое электрическое поле Фарадея, отличающееся от кулоновского, потенциального поля, создаваемого зарядом.

Электрическое поле любой природы действует на заряд q, его кинетический импульс изменяется согласно второму закону Ньютона

.

Интегрируем в пределах от 0 доt и получаем

.

Для поля Фарадея находим изменение импульса за время t

. (1.19)

Определяем полный импульс заряда q

, (1.20)

складывающийся из кинетического импульса частицы

и импульса магнитного поля, связанного с зарядом q:

.

Согласно (1.19), при изменении векторного потенциала сохраняется полный импульс

.

Ему сопоставляем оператор неизменной формы

. (1.20а)

Оператор имеет собственную функциюс фазойи с волновым числом. В результате фаза волновой функции и длина волны де Бройля в магнитном поле определяются полным импульсом. Получим следствия в рамках полуклассической квантовой механики.

Квазиклассическое квантование в магнитном поле. В формуле квантования Бора–Зоммерфельда при наличии магнитного поля импульс заменяется полным импульсом

,

, (1.21)

Условие максимума интерференции заряда в магнитном поле получил Вальтер Франц в 1939 г. Применим (1.21) к заряду в однородном магнитном поле.

Заряд в магнитном поле В, направленном по оси z. На заряд q, движущийся со скоростью, перпендикулярной полю, действует сила Лоренца

,

направленная по правилу левой руки, перпендикулярная магнитному полю, скорости V и кинетическому импульсу . Сила перпендикулярная скорости являетсяцентростремительной, тогда

.

Получаем радиус траектории

. (1.23)

Угловая скорость вращения, или циклотронная частота:

(1.24)

не зависит от скорости заряда.

Для однородного поля В находим векторный потенциал, используя

,

записанное в цилиндрических координатах

,

,

.

Для рассматриваемого поля

, ,,

получаем

, ,.

Следовательно, вектор А направлен по касательной к траектории заряда и связан с вектором В правилом правого винта.

Полный импульс

.

Для круговой траектории с номером , радиусомиз рисунка находим

. (1.24а)

Вычисляем циркуляции вдоль траектории n

,

.

Формула Бора–Зоммерфельда (1.21)

, ,

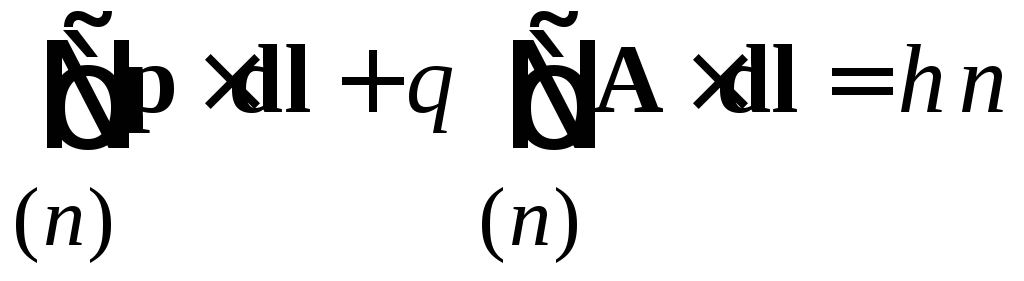дает условие квантования в магнитном поле – соотношение между радиусом и импульсом заряда на траектории n

. (1.25)

Квантование импульса и кинетической энергии. В (1.25) подставляем (1.23) и получаем

, (1.26а)

. (1.26б)

Спектр энергии эквидистантный и совпадает со спектром гармонического осциллятора с циклотронной частотой.

Квантование проекции момента импульса. Известно квантование проекции момента кинетического импульса

,

Получим квантование проекции момента полного импульса. Используем (1.24а)

,

и (1.25)

получаем

. (1.27)

Номер траектории определяется модулем момента полного импульса.

Квантование радиуса траектории. Из (1.23)

выражаем

,

подставляем в (1.26а)

,

получаем

, (1.29)

где магнитная длина

(1.30)

Для электрона

нм.

Для магнитного поля у земли

Тл, мкм.

Квантование траекторий электрона в магнитном поле наблюдалось экспериментально. Исследовалась пространственная структура состояний двухмерного газа электронов в поверхностном слое полупроводника InSb в магнитном поле В = 6 Тл. Использовался метод сканирующей туннельной спектроскопии (PRL 109, 116805 (2012)). При температуре Т = 0,3 К наблюдались концентрические кольца. Для такого газа из (1.29) и (1.30) получаем нм,нм,нм,нм.

Квантование магнитного потока. Используя (1.29)

,

находим магнитный поток через площадь, ограниченную траекторией:

, (1.31)

где квант магнитного потока

. (1.32)

Согласно (1.31) квантовое число n равно числу квантов магнитного потока, приходящихся на площадь, ограниченную траекторией заряда.

В сверхпроводнике заряд спаренных электронов , тогдаквант магнитного потока в сверхпроводнике

Тл м² (Вб). (1.33)

Ф₀ приблизительно равен потоку 1/100 магнитного поля земли через площадку диаметром 0,1 мм.

Квантование магнитного потока обосновали В.А. Фок и П. Иордан в 1930 г., Ф. Лондон в 1948 г. Экспериментально явление обнаружили в сверхпроводнике Б. Дивер и В. Фейрбэнк в 1961 г. Слой олова толщиной 0,3 10 мкм гальванически осаждался на кварцевой нити диаметром 13 мкм, получалось кольцо. При температуре выше сверхпроводящего перехода олова, равного 3,8 К, кольцо помещали в магнитное поле, направленное вдоль оси кольца. Температуру снижали, олово переходило в сверхпроводящее состояние и выталкивало поле из своего объема, создавая поверхностный кольцевой ток и магнитный поток через отверстие кольца. Результат измерений этого потока, где, соответствовал максимуму интерференции для фазы

, (1.34)

образованной волновой функцией куперовской пары с зарядом , проходящей по кольцу.

Квантование сопротивления. Рассмотрим контур с ничтожно малым активным сопротивлением. Плоскость контура пересекает поток магнитного поля Ф. К концам контура приложено напряжение U, по цепи идет ток I. При переносе по замкнутой цепи заряда q источник напряжения совершает работу .

При увеличении магнитного потока на , возникает явление электромагнитной индукции и для поддержания тока источник совершает дополнительную работу. Из закона сохранения энергии получаем

.

В цепи возникает индуктивное сопротивление

. (1.35)

Если ток переносится в сверхпроводнике куперовскими парами электронов с зарядом , то кванту магнитного потока

соответствует квант сопротивления

кОм. (1.36)

Кванту потока

соответствует холловское сопротивление

кОм. (1.36а)

Квантование сопротивления баллистического проводника, в котором электроны движутся без рассеяния:

,

где – число активизированных поперечных мод движения, которые дают вклады в продольный ток, обосновал Рольф Ландауэр в 1970 г.

Интерференционные осцилляции сопротивления проводника с двумерным электронным газом при изменении магнитного поля экспериментально исследовали Юрий Васильевич и Дмитрий Юрьевич Шарвины в 1981 г. Использовалось кольцо из магния диаметром (1,52) мкм. При температуре ~1К длина свободного пробега электронов превышает размер кольца. Электрон движется баллистически без рассеяния, фаза волновой функции меняется регулярно. На платиновые контакты А и В подается напряжение. Через кольцо проходит магнитный поток Ф. На контакте А электронная волна разделяется и идет по путям 1 и 2, набирая фазы θ₁ и θ₂, и интерферирует на контакте В с разностью фаз .

Учитывая, что при обращении движения набираемая фаза меняет знак, можно считать, что электрон делает один оборот по кольцу. Из (1.34)

получаем

, .

Изменение магнитного потока на меняет разность фаз

.

Максимум интерференции соответствует максимуму тока между контактами. В результате при изменении магнитного поля сопротивление между контактами осциллирует с периодом

.

Если через кольцо одновременно переносится заряд , то период осцилляций равен. Эксперимент подтвердил этот вывод.

Квантование магнитного момента. Ток в контуре создает магнитный момент, равный произведению силы тока на площадь контура и направленный перпендикулярно плоскости контура по правилу правого винта.

Магнитный момент пропорционален моменту импульсаL заряда, создающего ток:

,

где –гиромагнитное отношение, известное из классической физики. Используя (1.27)

,

получаем орбитальный магнитный момент электрона

,

, (1.37)

где магнетон Бора

(1.38)

введен В. Паули в 1920 г. Проекция орбитального магнитного момента на направление поля квантуется и пропорциональна магнитному квантовому числу m.

Подстановка импульса. В магнитном поле длина волны де Бройля определяется полным импульсом . При изменении поля меняется векторный потенциалA и скорость заряда за счет явления электромагнитной индукции, полный импульс сохраняется и ему сопоставляется оператор неизменной формы

. (7.12)

Действие магнитного поля на квантовую систему учитывается подстановкой импульса

. (7.13)

В формулах, описывающих систему без магнитного поля, оператор кинетического импульса заменяется выражением(7.13). Электрическое поле со скалярным потенциалом учитывается дополнительным слагаемым потенциальной энергии

. (7.14)

Операторы физических величин. С учетом (7.13) и (7.14) получаем гамильтониан, уравнение Шредингера и плотность тока вероятности в электромагнитном поле

, (7.17)

, (7.18)

. (7.19)

Соотношения неопределенностей для проекций скорости. Используя (7.13)

и

, ,,

находим коммутационные соотношения

,

,

. (7.21)

Операторы проекций кинетического импульса заряда в магнитном поле не коммутируют.

Для операторов скорости

, ,

из (7.21) получаем

,

,

.

Некоммутативность операторов приводит к соотношениям неопределенностей

,

,

. (7.22)

Проекции скорости заряда в магнитном поле определяются одновременно с ограниченной точностью.