Одномерные стационарные системы

Уравнение Шредингера (2.57) для двухмерных и трехмерных стационарных систем

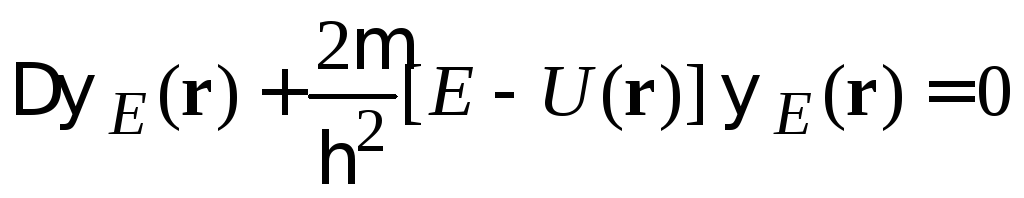
сводится в ряде случаев к одномерному уравнению (2.59)

, (3.1)

или

, (3.2)

где волновое число

связано с длиной волны де Бройля

.

Для электрона массой с энергией, выраженной в эВ, получаем

.

При волновое число , длина волны электрона порядка ангстрема.

Переход к одномерной задаче. В декартовых координатах стационарное уравнение Шредингера (2.57) для частицы массой μ с полной энергией Е в поле с потенциальной энергией имеет вид

.

Если потенциальная энергия является суммой слагаемых с разными аргументами

,

То трехмерное уравнение разделяется на независимые одномерные уравнения, волновая функция факторизуется

.

Движения частицы в проекциях на оси x, y, z происходят независимо. При подстановке функции в уравнение, деленное на , получаем уравнения

, ,

где

; .

Энергия частицы складывается из энергий независимых движений

.

Частные случаи одномерных стационарных состояний

Свободная частица при отсутствии внешнего поля описывается уравнением (3.2)

с волновым числом

.

Общее решение

(3.3)

является суперпозицией бегущих волн

,

распространяющихся по- и против оси x с комплексными амплитудами . Если краевые условия не накладываются, то спектр k непрерывный и энергия .

Движение частицы создает плотность тока вероятности. В (2.72)

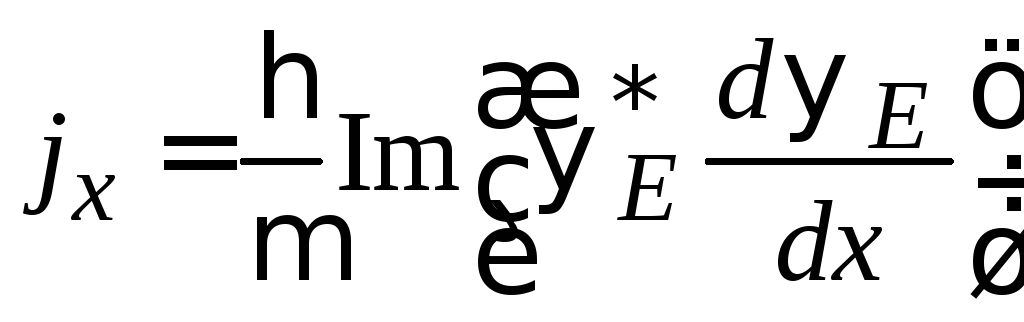
подставляем (3.3) и находим

где 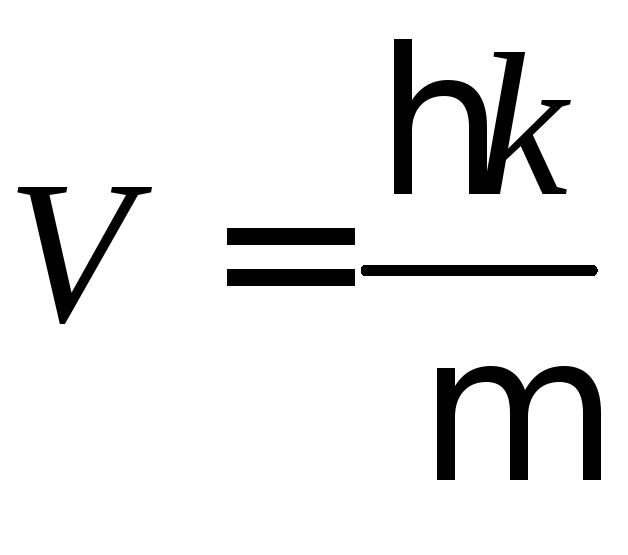– скорость частицы. В круглой скобке сумма двух последних слагаемых чисто мнимая, в результате проекция плотности тока вероятности на осьx

,

, . (3.6)

Для частицы с зарядом е и энергией Е задаем плотности электрического тока , получаем плотности тока вероятности, и находим модули амплитуд волн.

Частица в потенциальном ящике. Для частицы ящик размером L является потенциальной ямой. Внутри ящика потенциальная энергия и частица с энергиейЕ описывается уравнением (3.2)

,

где

.

Уравнению удовлетворяет решение в виде бегущих волн

(3.7а)

с комплексными амплитудами , илистоячих волн

(3.7б)

с вещественными . Стоячие волны возникают при сложении бегущих волни. Решение (3.7б) вещественно.

Стенки ящика создают потенциальный барьер и ограничивают возможные значения волнового числа k и энергии Е. Если не существенны явления на стенках и не известна форма потенциальной энергии барьеров, то вместо одного ящика рассмотрим систему повторяющихся ящиков. Тогда решение удовлетворяет периодическому условию Борна–Кармана

. (3.8)

При подстановке (3.7а) условие выполняется при

.

Используя

, ,

находим

.

Следовательно, квантуются волновое число, импульс и энергия частицы

,

.

,

где –квантовое число. Длина волны де Бройля на уровне n

,

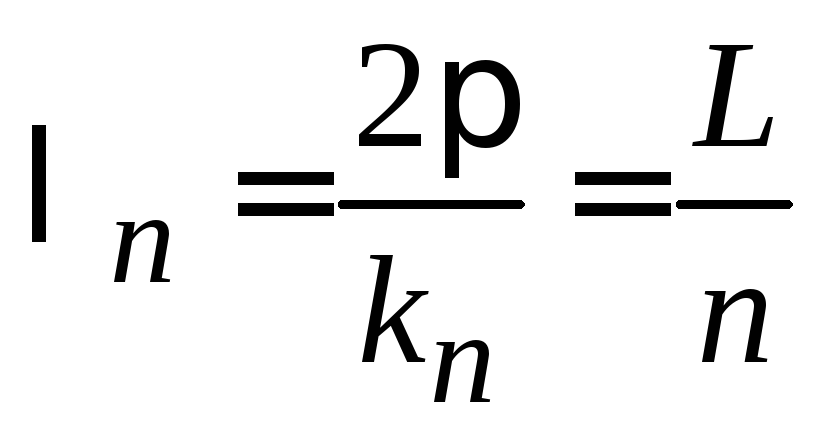тогда показывает число длин волн, укладывающихся на длине ящика, или число полуволн, приходящихся на длину траектории. Расстояние между уровнями

.

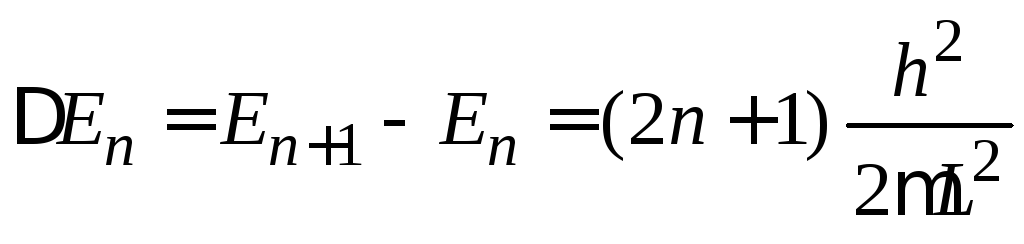Для кристалла с характерным размером получаем. Сравниваем с тепловой энергией частицы газа при нормальной температуре

.

При высокой температуре и большом ящике тепловая энергия превышает расстояние между уровнями, дискретность спектра не проявляется и спектр энергии квазинепрерывный.

При низкой температуре и малом ящике тепловой энергии не хватает для перевода частицы между уровнями и существенна дискретность спектра.

Состояние n занимает в координатном пространстве объем, равный размеру ящика:

,

в импульсном пространстве неопределенность

,

в фазовом пространстве

. (3.9)

Любое состояние, находящееся в одномерном потенциальном ящике, занимает фазовый объем, равный постоянной Планка – основное положение статистической теории, следующее из соотношения неопределенностей.

Частица в потенциальной яме. Если потенциальная энергия имеет минимум, меньший значений при, которые считаем одинаковыми и равными нулю, то это потенциальная яма.

При полной энергии частицы ее движение не ограничено стенками ямы, она свободна, энергия имеет непрерывный спектр, яма лишь рассеивает частицу. Свободное состояние является бегущей волной и описывается комплексной функцией.

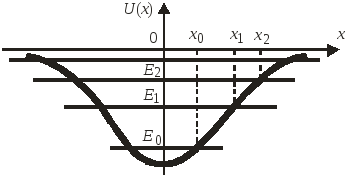
При состояние связанное, частица захвачена ямой. Потенциальными ямами для электрона являются: атом, кусок металла или полупроводника, квантовая точка, осциллятор и т.д.

Свойства связанных состояний. При частица находится в ограниченных пределах и имеет дискретный спектр, где–главное квантовое число. Состояние с наименьшей энергией E₀ называется основным, остальные – возбужденные. Функции связанных состояний вещественные и являются стоячими волнами. Спектр состояний одномерной ямы невырожденный – состояния с разными волновыми функциями имеют разные энергии.

Для симметричной ямы

,

где является точкой симметрии потенциальной энергии, уравнение Шредингера

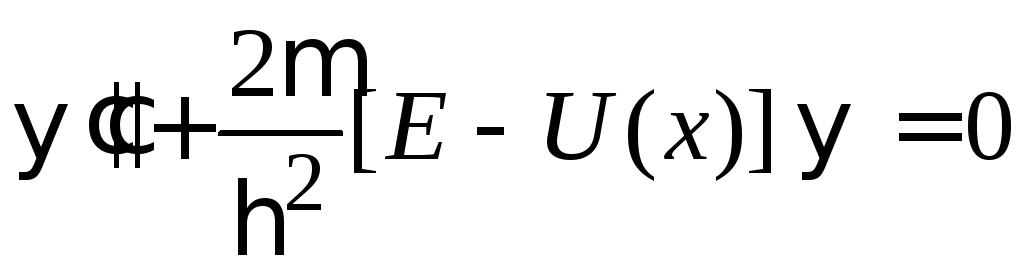
не изменяется при замене . Множество общих решений распадается на линейно независимые и взаимно ортогональные подмножества четных и нечетных решений

,

,

,

.

Число нулей волновой функции на протяжении ямы является номером состояния и называется главным квантовым числом Оно определяет длину волны , импульси полную энергиючастицы. С ростомn уменьшается , увеличиваютсяи.Между двумя последовательными нулями функции состояния находится нуль соседнего по энергии состояния.

Множество связанных состояний образует ортонормированный базис

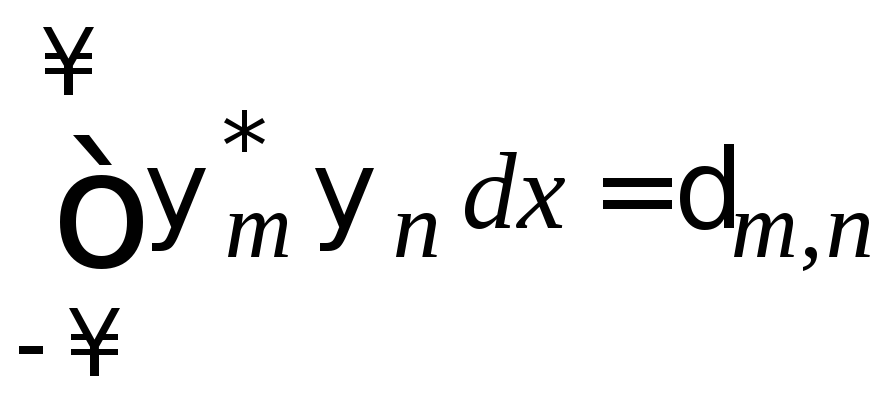. (3.20)

Произвольное состояние частицы в яме разлагается по этому базису, является суперпозицией состояний с разными энергиями. Частицу в таком состоянии можно обнаружить с некоторой вероятностью на любом уровне.

Борновский параметр. В яме с характерной шириной L из соотношения неопределенностей

,

где , получаем характерный импульс и кинетическую энергию частицы

, .

Мера воздействия ямы на частицу определяется безразмерным борновским параметром, показывающим насколько велика энергия ямы по сравнению с кинетической энергией частицы:

, (3.22)

где – характерная глубина ямы. При яма слабая, прияма сильная.

Частица в области, недоступной для классического движения. На краю ямы при полная энергия частицы равна потенциальной энергией, кинетическая энергия и импульс обращаются в нуль, классическая частица останавливается. Привыполняется

,

кинетическая энергия – отрицательная, импульс– мнимый, поэтому приклассическая частица не существует.

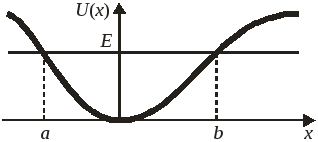
Для квантовой частицы уравнение Шредингера

при ,получает вид

(3.23)

с вещественным коэффициентом затухания

.

Уравнение имеет не равное нулю решение. Квантовая частица обнаруживается вне потенциальной ямы с некоторой вероятностью благодаря туннельному эффекту. При ,общее решение (3.23) имеет вид

, .

Нормировка

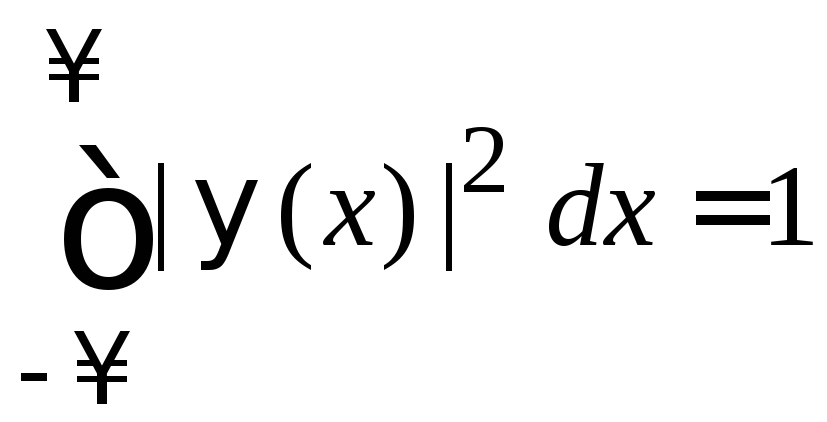
в области выполняется только для убывающего с ростом x частного решения. Поэтому полагаем и получаем

.

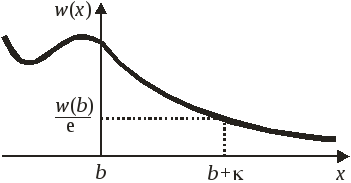
Плотность вероятности обнаружения частицы

экспоненциально уменьшается при удалении от края ямы, где характерное расстояние затухания

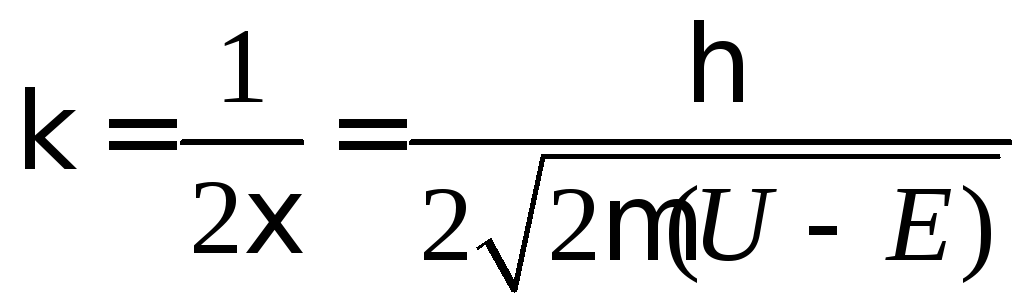
– характерное расстояние от края ямы, до которого еще вероятно обнаружить частицу. Чем выше уровень энергии E, тем дальше от края ямы можно обнаружить частицу.

В частности

, ,

где κ – расстояние от края ямы до места, где вероятность обнаружения частицы уменьшается в раз. Чем ниже уровень энергии, тем больше , тем меньше κ и быстрее уменьшается вероятность с удалением от края ямы.