ЭрмитовыЙ оператор

Физическая величина должна быть вещественной, а ее измерение – однозначным. Эти условия для собственных значений обеспечивает эрмитовый оператор. Операция эрмитового сопряжения определяется через интегральную квадратичную форму. Такая форма описывает, в частности, среднее значение измеряемой величины.

Эрмитово сопряженный оператор обозначается значком «+» и определяется в виде

. (2.11)

Интегрирование проводится по всему объему пространства, занятого частицей.

Свойства эрмитового сопряжения

,

,

,

, . (2.12)

Для доказательства применяем (2.11) к оператору

и последовательно к оператору , и затем к:

.

Сравниваем правые стороны равенств.

Эрмитовый оператор не изменяется при эрмитовом сопряжении

. (2.13)

Из (2.11) получаем определение эрмитового оператора

. (2.14)

Свойства эрмитова оператора:

1) Собственные значения вещественные.

Доказательство:

В (2.14) полагаем , где– собственная функция оператора. Учитываем

, ,

получаем

.

Следовательно,

(2.15)

– измеряемая величина вещественна.

2) Собственные функции, соответствующие разным собственным значениям, взаимно ортогональны.

Доказательство:

Для собственных функций иоператоравыполняется

, ,,.

Из (2.14)

при ,получаем

.

Учитывая вещественность собственных значений (2.15), находим

.

При выполняетсяусловие ортогональности состояний

. (2.16)

Следовательно, состояния ипри измерении не совместимы и измерение однозначно.

Эрмитовость оператора импульса

Докажем

.

В равенстве (2.14)

левая сторона с оператором имеет вид

.

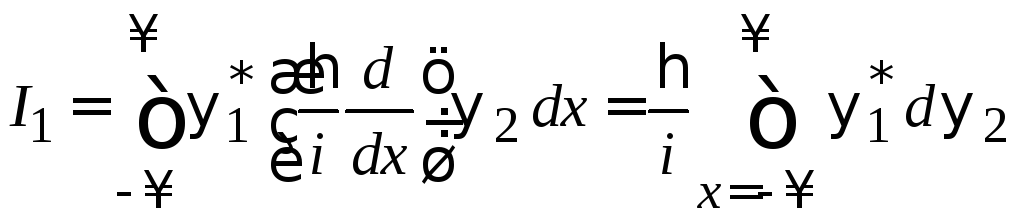Вычисляем правую сторону (2.14)

.

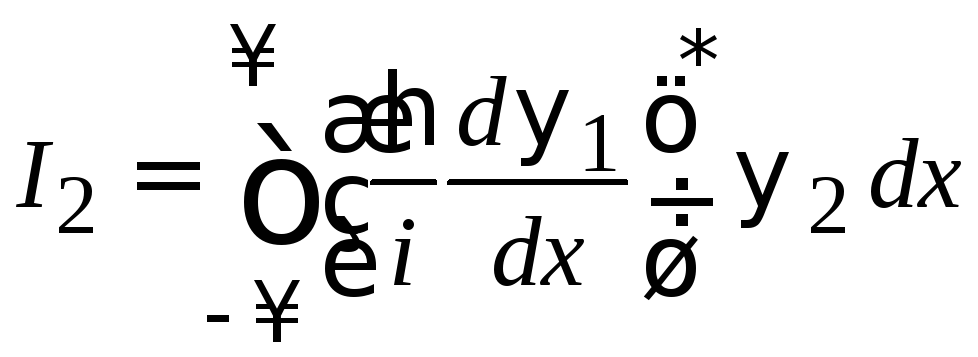
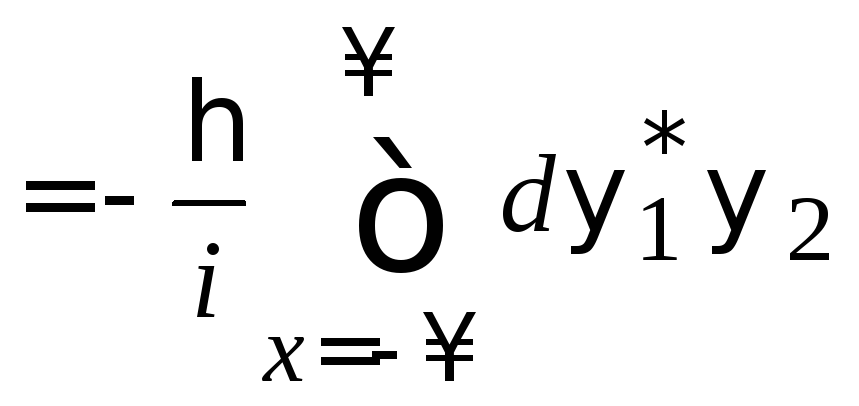В результате

.

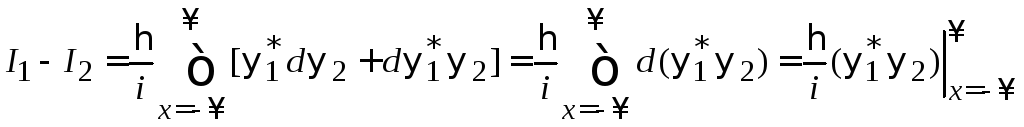Волновые функции квадратично интегрируемы и равны нулю на бесконечности, поэтому , и доказана эрмитовость оператора импульса.

УсЛовия ортонормированности

Множество собственных функций любого эрмитового оператора образует ортонормированный базис. Спектр базиса зависит оти может быть дискретным или непрерывным. Нормировка ортазависит от вида спектраn. Ортогональность ортов , где, и их нормировку объединяет условие ортонормированности.

Дискретный спектр n. Нормировка следует из условия ортонормированности

, (2.21)

где 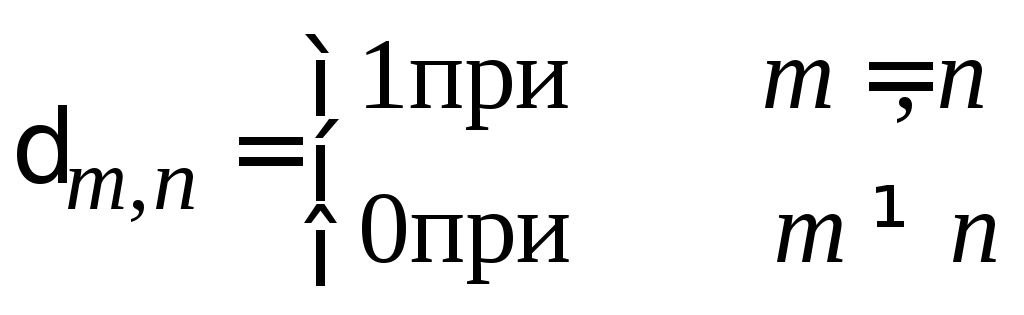–символ Кронекера. Сходимость интеграла требует достаточно быстрого убывания плотности вероятности за пределами конечного объема. Следовательно, дискретный спектр соответствует связанному состоянию, и наоборот – связанное состояние имеет дискретный спектр энергии и импульса.

Непрерывный спектр n. Если индекс собственной функции принимает непрерывные значения, то в (2.21) вместо символа Кронекера ставится дельта-функция

. (2.22)

При интеграл стремится в бесконечность. Плотность вероятностиконечна во всех точках. Чтобы обеспечить требуемое значение интеграла она не может равняться нулю за пределами любого конечного объема. Следовательно,непрерывный спектр соответствует неограниченному движению, и наоборот – состояние неограниченного движения имеет непрерывный спектр энергии и импульса.