
Красюк конспект лекций
.pdf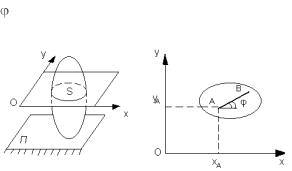
Л е к ц и я 6
ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК ТЕЛА
Плоскопараллельное движение твердого тела. Разложение плоского движения твердого тела на поступательное и вращательное. Уравнение плоского движения. Теорема о скоростях точек твердого тела, ее следствия. Определение скоростей точек твердого тела с помощью мгновенного центра скоростей. План скоростей.
Плоскопараллельным (или плоским) называется такое движение твердого тела, при котором все его точки перемещаются параллельно некоторой фиксированной плоскости.
Плоское движение совершают многие части механизмов и машин (кривошипно-ползунный механизм, колесо, катящееся по рельсу, и т. п.). Для изучения движения всего тела достаточно изучить, как движется в плоскости xyz сечение S этого тела.
Положение фигуры S в плоскости XOY определяется положением какого-нибудь отрезка AB , проведенного на этой фигуре (рис. 1). В свою очередь, положение отрезка AB можно определить, зная коорди-
наты xA, yA, (рис. 2). Точку A , выбранную для определения положения фигуры S , будем называть полюсом.
Рис. 1 |
Рис. 2 |
51
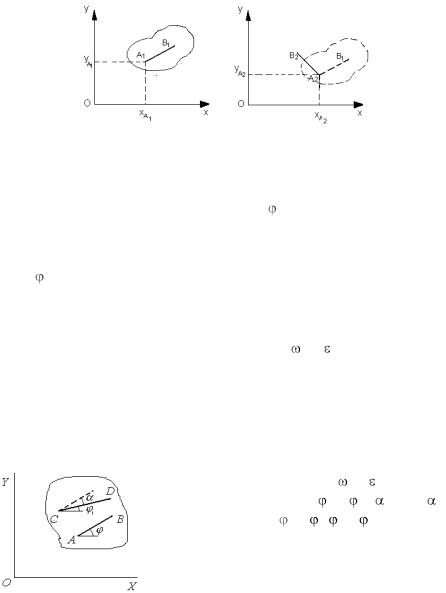
Рис. 3 |
Рис. 4 |
Чтобы знать закон движения фигуры, необходимо знать зависи- |
|
мости |
|
xA = f1(t) , yA = f2 (t) , |
= f3 (t) . |
Это уравнения движения плоской фигуры в ее плоскости. Первые два уравнения определяют поступательное движение полюса
(при |
= const ) (рис. 3), а третье уравнение определяет вращатель- |
|||||
ное |
движение фигуры |
вокруг |
полюса |
|
(xA = const , yA = const) |
|
(рис. 4): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Vпоступ |
= VA , |
aпоступ = aА |
, |
и . |
|
В качестве полюса можно выбрать любую точку фигуры, например C, и определить положение фигуры отрезком СD (рис. 5). Ха-
рактеристика поступательного движения изменится, так как в об- |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
щем случае VC |
№ VA |
и aC |
№ aА |
(иначе |
движение |
было |
бы |
|||||
|
|
поступательным). Характеристики враща- |
||||||||||
|
|
тельной части движения ( |
и |
) |
остаются |
|||||||
|
|
неизменными, так как |
1 = |
– |
, |
где |
= |
|||||
|
|
const. |
Поэтому |
|
1 |
= , |
|
= . |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
За полюс принимается такая точка, скорость которой либо задана, либо ее легко определить из условия задачи.
Вращательная часть движения от выбора полюса не зависит.
52
Определение скоростей точек плоской фигуры
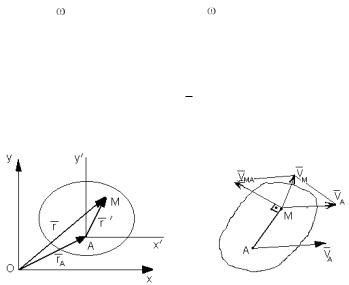
Пусть оси Y ўAX ў движутся вместе с точкой A , оставаясь параллельными осям XOY (рис. 6). Тогда положение точки M будет определяться радиусом-вектором r:
r = rA + r ў,
где r ў = AM . Тогда скорость точки определяется выражением
|
|
V |
|
= |
dr |
= |
drA |
|
+ |
dr ў |
. |
|||
|
|
|
|
|
|
|
||||||||
|
|
M |
|
|
dt |
dt |
|
dt |
||||||
|
|
|
|
|
|
|
||||||||
В |
полученном |
равенстве |
|
|
drA |
= V |
|
– скорость полюса A , |
||||||
|
|
|
|
|||||||||||
|
|
|
|
|
|
dt |
A |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
dr |
ў / dt = VMA – |
скорость, которую точка M получает при rў = const , |
||||||||||||
т.е. при вращении плоской фигуры относительно точки A (полюса): |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
VM |
|
= VA |
+VMA. |
||||||||
При этом VMA = |
MA (VMA ^ MA) , где |
|
– угловая скорость фигуры. |
|||||||||||
Скорость любой точки M плоской фигуры геометрически складывается из скорости какой-нибудь другой точки А, принятой за полюс, и скорости, которую точка М получает при вращении фигуры вокруг этого полюса (рис. 7).
Модуль и направление скорости VM находятся построением параллелограмма.
Рис. 6 |
Рис. 7 |
53
Теорема о проекциях скоростей двух точек тела. Проекции ско-
ростей двух точек твердого тела на ось, проходящую через эти точки, равны друг другу, т.е.
VA cos = VB cos .
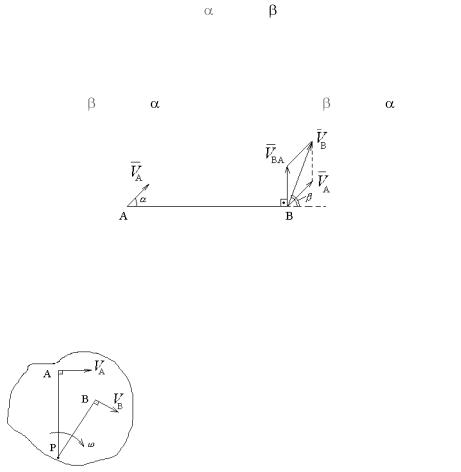
Д о к а з а т е л ь с т в о. Разложим |
скорость |
V |
на две состав- |
|
|
|
|
B |
|
ляющие в соответствии с равенством VB |
= VA |
+VBA (рис. 8). Проеци- |
||
руя обе части равенства на ось, проходящую через точки A и B , по- |
||||
лучим VB cos = VA cos +VBA cos90° или VB cos |
= VA cos . |
|||
Рис. 8
Мгновенный центр скоростей
Мгновенным центром скоростей называется точка плоской фигу-
ры, скорость которой в данный момент времени равна нулю.
Если тело движется непоступательно, то такая точка существует и при этом она единственная.
Пусть в момент времени t скорости точек А и В плоской фигуры будут не параллельны, тогда точка Р будет мгновенным центром ско-
ростей, так как по теореме о проекциях VP
|
должна одновременно проецироваться в точку |
|||
|
на отрезки АР и РВ (рис. 9). Это возможно, |
|||
Рис. 9 |
если V |
= 0 . Если за полюс взять точку Р, то |
||
|
|
P |
|
|
|
VA |
= VP +VPA |
= VPA , |
|
так как VP = 0 .
54

Скорости точек плоской фигуры в данный момент времени определяются так, как если бы фигура вращалась вокруг мгновенного центра
скоростей: |
|
|
|
|
|
|
|
VA = PA (VA ^ РА) , |
VB = PB (VB ^ PB), |
||||||
|
VA |
= |
VB |
= ... = |
VN |
= . |
|
|
P A |
PB |
PN |
||||
|
|
|
|
|
|||
Скорости точек плоской фигуры пропорциональны их расстояниям от мгновенного центра скоростей.
Выводы
1.Для определения мгновенного центра скоростей достаточно знать только направления скоростей VA и VB каких-нибудь двух точек
Аи В плоской фигуры.
2.Для определения скорости любой точки плоской фигуры необходимо знать модуль и направление скорости какой-нибудь одной точки А фигуры и направление скорости другой ее точки В.
3.Угловая скорость плоской фигуры равна в каждый данный момент времени отношению скорости какой-нибудь точки фигуры к ее расстоянию до мгновенного центра скоростей Р.
Частные случаи определения мгновенного центра скоростей
1. Если движение осуществляется путем качения (без скольжения) одного цилиндрического тела по поверхности другого неподвижного тела, то точка Р катящегося тела, касающаяся неподвижного тела, имеет скорость VP = 0 и, следовательно, является мгновенным центром скоро-
стей (рис. 10).
2. Если скорости точек А и В параллельны друг другу, причем линия AB не перпендикулярна к векторам скоростей, то мгновенный центр скоростей находится в бесконечности, а движение в данный момент времени поступательное (рис. 11).
55
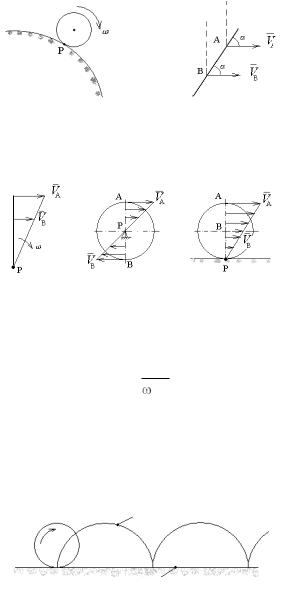
Рис. 10 |
Рис. 11 |
3. Если скорости точек А и В параллельны друг другу и при этом АВ перпендикулярна к векторам скоростей, то мгновенный центр скоростей Р определяется построением, показанным на рис. 12.
Рис. 12
4. Если известны вектор скорости точки А и угловая скорость тела, то положение мгновенного центра скоростей Р, лежащего на перпендикуляре к вектору скорости точки А, можно найти из равенства
AP = VA .
ВА
При движении плоской фигуры мгновенный центр скоростей непрерывно изменяет свое положение как на неподвижной плоскости, так и на подвижной, связанной с плоской фигурой. Геометрическое место мгновенного центра скоростей на неподвижной плоскости назы-
вают неподвижной центроидой, а на плоской фигуре – подвижной центроидой (рис. 13).
Подвижная центроида
Неподвижная центроида
Рис. 13
56
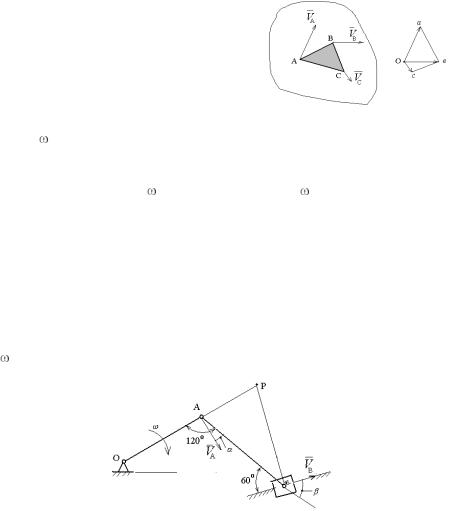
План скоростей
Планом скоростей называется диаграмма, на которой от некоторого центра отложены векторы скоростей точек тела (рис. 14).
Пусть VA ,VC и VB – скорости соответствующих точек тела. Векто-
ры скоростей, соответствующие в |
|
|
|
|
|
|
|
|||||||||||
некотором масштабе отрезкам опре- |
|
|
|
|
|
|
|
|||||||||||
деленной длины, отложим от произ- |
|
|
|
|
|
|
|
|||||||||||
вольно выбранного центра О, тогда |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Oа = VA, |
|
Oс = VC , |
Ob |
= VB . |
|
|
|
|
|
|
|
||||||
|
Допустим, что точка А – полюс, |
|
|
|
|
|
|
|
||||||||||
тогда V |
|
= V |
+V |
, где V |
|
^ BA , |
|
|
|
|
Рис. 14 |
|
||||||
|
B |
|
A |
BA |
|
BA |
|
|
|
|
|
|
|
|
|
|
||
V |
= |
|
BA . Из диаграммы видно, |
|
|
|
|
|
|
|
||||||||
BA |
ВА |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
что |
Ob |
= Oa |
+ ab или |
VB = VA |
+ ab , |
следовательно ab = VBA |
, тогда |
|||||||||||
|
^ AB . Так как ab = |
ВА AB, |
то |
ab |
|
= |
ac |
= |
ВА . |
|
|
|||||||
ab |
|
|
|
|||||||||||||||
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
AB |
AC |
|
|
|
|||
|
Отрезки, соединяющие концы векторов скоростей на плане скоро- |
|||||||||||||||||
стей, перпендикулярны к отрезкам, соединяющим соответствующие точки тела, и по модулю пропорциональны этим отрезкам.
План скоростей позволяет получить скорость любой точки тела. План скоростей механизма строится как совокупность планов скоростей отдельных его звеньев (тел), причем все векторы скоростей откладываются от общего центра О, называемого полюсом плана скоростей.
Задача. Определить скорость ползуна В для показанного на рис. 15 положения механизма, если угловая скорость кривошипа ОА равна
= 10 рад/с, OA = r = 0,1 м . Решение выполнить двумя способами:
Рис. 15
57
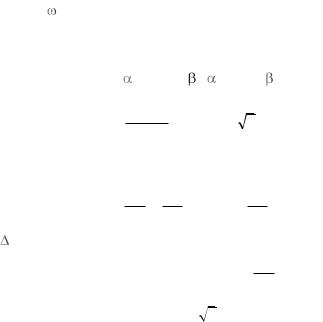
1)с использованием теоремы о проекциях скоростей двух точек тела;
2)построением мгновенного центра скоростей шатуна AB .
Решение.
1. VA = OA = 10 Ч0,1 = 1 м/c , VA ^ OA .
Так как скорость VB направлена вдоль оси ползуна, то по теореме о проекциях скоростей имеем
VA cos = VB cos , = 30° , = 60°,
VB = VA cos60cos30°° = 1tg60° = 
 3 » 1,73 м/c .
3 » 1,73 м/c .
2. Найдем положение мгновенного центра скоростей (точка Р), тогда
VAPA = VBPB , VB = VA BPAP .
APB – прямоугольный, так как
РABP = 30° , РBAP = 60° Ю BPAB = tg60°,
VB = 1tg60° = 
 3 » 1,73 м/c .
3 » 1,73 м/c .
58
Л е к ц и я 7
ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА.
ОПРЕДЕЛЕНИЕ УСКОРЕНИЙ ТОЧЕК ТЕЛА
Теорема о сложении ускорений
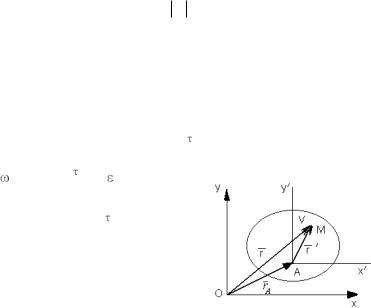
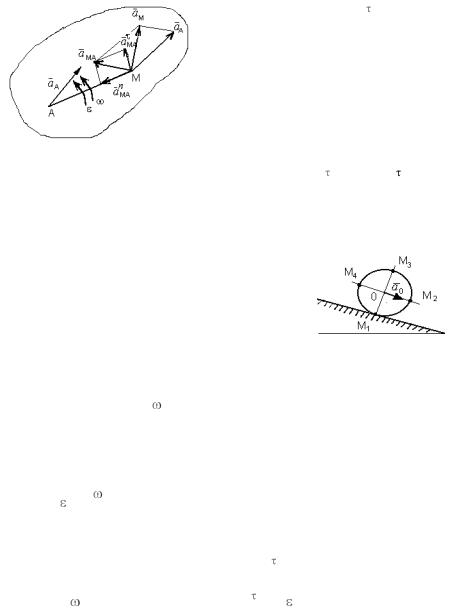
Пусть тело совершает плоское движение в координатах xOy. Требуется определить ускорение точки М (рис. 1). Обозначим полюс точ-
кой А и через него проведем оси yўxў , которые движутся вместе с по-
люсом А, оставаясь параллельными осям x и y. Обозначим положение точек А и М радиусами-векторами:
r = rA + r ў , где r ў = AM ,
тогда
d |
2 |
|
|
d |
2 |
|
d |
2 |
|
ў |
|
|
|
|
|
|
|
r |
|
|
r |
|
r |
|
|
||||||||
|
|
|
= |
|
|
A |
+ |
|
|
|
|
или |
a |
= a |
|
+ a . |
|
|
|
|
|
|
|
|
|
|
A |
||||||
dt2 |
|
dt2 |
dt2 |
|
|
M |
|
MA |
||||||||
|
|
|
|
|
|
|
||||||||||
Так как aМА – ускорение во вращательном движении точки М вокруг точки А, то
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
aMA |
= aMA + aMA |
, |
|
где aMAn |
= |
2MAMA , |
aMA = MAMA . |
|
|
||||
Таким образом, |
|
|
|
|
|
||||
|
|
|
|
n |
|
|
|
|
|
|
a |
= a |
A |
+ a |
MA |
+ a . |
|
|
|
|
M |
|
|
MA |
|
|
|
||
Ускорение любой |
точки |
M плоской |
|
||||||
фигуры |
геометрически |
складывается |
из |
|
|||||
ускорения какой-нибудь |
другой точки |
А, |
|
||||||
принятой за полюс, и ускорения, которое |
|
|
точка М получает при вращении фигуры |
Рис. 1 |
|
вокруг этого полюса. |
||
|
||
59 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При |
этом |
вектор |
|
aMA |
направлен |
||||||
|
перпендикулярно к отрезку МА в сторо- |
|||||||||||
|
ну вращения, если движение ускорен- |
|||||||||||
|
ное, и против вращения, если движение |
|||||||||||
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
замедленное. |
|
Вектор |
aMA |
всегда на- |
|||||||
|
правлен от точки М к точке А (рис. 2). |
|||||||||||
|
В общем случае, если движение |
|||||||||||
|
полюса А является криволинейным, |
|||||||||||
Рис. 2 |
получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
n |
|
|
. |
|||
|
a |
= a |
А |
+ a |
А |
+ a |
MA |
+ a |
MA |
|||
|
M |
|
|
|
|
|
|
|
||||
Задача. Колесо катится без скольжения в вертикальной плоскости по наклонному прямолинейному пути (рис. 3). Найти ускорение концов двух
взаимно перпендикулярных диаметров коле- |
|
||
са, из которых один параллелен рельсу, если в |
|
||
рассматриваемый момент |
времени скорость |
|
|
центра колеса VO = 1 м/с , |
ускорение центра |
|
|
|
= 3 м/c2 , радиус колеса R = 0,5 м . |
|
|
колеса a |
|
||
O |
|
|
|
Решение. Точка M1 – мгновенный центр |
|
||
скоростей, следовательно, угловая скорость |
Рис. 3 |
||
колеса равна
|
|
|
|
|
|
|
= |
|
VO |
|
= |
|
1 |
|
= 2 c-1 . |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
OM1 |
|
0,5 |
|
|
|
|
|
|
|
|
|
|
||||
Угловое ускорение колеса |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
ж |
V |
ц |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d з |
|
O |
ч |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dV0 |
|
|
aO |
|
|
|
|
|
||||
|
= |
|
d |
= |
и OM1 |
ш |
|
= |
|
1 |
|
|
|
= |
= |
3 |
= 6 c |
-2 |
. |
|||||||
|
|
dt |
|
|
dt |
|
|
OM1 |
dt |
|
OM1 |
0,5 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Примем за полюс точку О, тогда |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
, |
|
|
|
|
|
||||
|
|
|
|
|
|
|
a |
|
= a |
|
+ a |
+ a |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
M |
|
|
|
O |
|
|
|
MO |
|
MO |
|
|
|
|
|
|
|||
где an |
= |
2MO = 22 |
Ч0,5 = 2 м/с2 ; |
a |
|
|
= MO = 6Ч0,5 = 3 м/c2 . |
|||||||||||||||||||
MO |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
MO |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
60 |
|
|
|
|
|
|
|
|
|
|
||
