
Красюк конспект лекций
.pdf
ние |
M ў |
и в этих точках имеет соответственно скорости |
|
и |
|
ў , |
|
V |
V |
||||||
|
|
|
|
|
|
|
|
dV |
= V |
ў -V . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 7 |
|
|
|
|
|
|
|
|
|||
В этом случае |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
a |
|
|
|
(dV ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
= |
|
|
|
|
|
– касательное ускорение, |
|
|
|||||||||||||
|
|
|
|
|
|
dt |
|
|
|
||||||||||||||||
|
|
|
|
a |
= |
(dV )n |
|
– нормальное ускорение. |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
n |
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Перенесем вектор V ў |
в точку M , при этом |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
dV = AB, V |
= |
MA, V ў = MB . |
|
|
|
|||||||||||||
|
При |
t ® 0 приращение угла d |
|
также стремится к нулю, а фигу- |
|||||||||||||||||||||
ра ADBC стремится к прямоугольнику, в котором диагональ AB |
|||||||||||||||||||||||||
стремится |
|
к |
AC . |
Так |
как |
|
|
AC = DB , |
MA = MD |
, то |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
. Но AC – проекция |
|
на касательную, |
|||||||||||
dV |
=V ў -V |
= MB - MD = AC |
dV |
||||||||||||||||||||||
т.е. (dV )r |
= AC , тогда dV = (dV )r , следовательно, |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
a |
= |
dV |
|
= |
d 2s |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
dt2 |
|
|
|
|
|||||||
Далее, AD – это проекция |
|
|
на нормаль, т. е. |
AD = (dV )n |
можно |
||||||||||||||||||||
dV |
|
||||||||||||||||||||||||
рассматривать |
как |
|
|
|
элементарную |
|
дугу |
радиуса |
MA , |
тогда |
|||||||||||||||
AD = MAd |
= Vd |
|
и, следовательно, |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
= |
Vd |
. |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
41 |
|
|
|
|
|
|
|
|
||
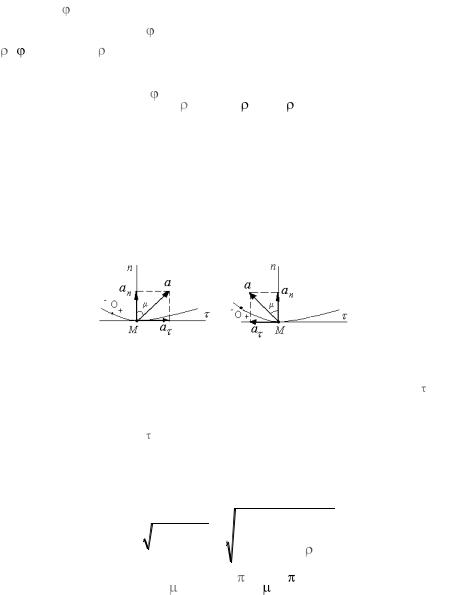
Угол |
между касательной и кривой в двух ее точках называется |
|||||||
углом смежности, d |
– |
элементарный |
угол смежности, тогда |
|||||
d = dS , где – радиус кривизны траектории. В этом случае |
||||||||
|
|
|
dS |
|
VdS |
|
V 2 |
|
|
d |
= |
|
, a = |
|
= |
|
. |
|
|
|
|
|||||
|
|
|
|
n |
dt |
|
|
|
|
|
|
|
|
|
|
|
|
Тангенциальное (касательное) ускорение (проекция ускорения точки на касательную) равна первой производной от числового значения скорости или второй производной от расстояния (криволинейной координаты) по времени. Нормальное (центростремительное) ускорение (проекция ускорения на главную нормаль) равна квадрату скорости, деленному на радиус кривизны траектории в данной точке кривой (рис. 8).
|
|
Рис. 8 |
|
|
|
|
|
|
|
Пусть точка |
M движется по кривой. Изобразим векторы an |
, a , a . |
||
|
|
|
|
|
Вектор нормального ускорения an всегда направлен в сторону вогну- |
||||
|
|
|
|
|
тости кривой. Вектор a |
направлен по касательной к траектории как в |
|||
сторону скорости (ускоренное движение), так и противоположно ей (замедленное движение).
Полное ускорение точки
|
|
|
|
|
ж dV ц |
2 жV 2 ц2 |
|
||||
|
2 |
|
2 |
|
|||||||
a = |
an |
+ ar |
|
= |
з |
|
ч |
+ з |
|
ч |
, |
|
|
|
|||||||||
|
|
|
|
|
и |
dt ш |
и |
|
ш |
|
|
tg = |
ar |
, - |
|
Ј |
Ј |
|
. |
|
|
|
|||||
|
an |
2 |
|
2 |
|
||
42 |
|
|
|
|
|
||

Частные случаи движения точки
1. Прямолинейное движение точки. Траектория – прямая, следова-
|
|
|
|
|
|
V 2 |
|
||
тельно, ρ = Ґ |
, тогда a |
|
= |
|
|
= 0 . |
Поэтому полное ускорение равно |
||
|
|
||||||||
|
|
|
n |
|
|
|
|
|
|
касательному: |
a = a = |
dV |
. |
|
|||||
dt |
|
||||||||
|
|
|
|
|
|
|
|
||
2. Равномерное движение точки. В этом случае V = const , следо- |
|||||||||
вательно, a = |
dV |
= 0 , |
|
поэтому полное ускорение равно лишь нор- |
|||||
|
|
||||||||
|
|
dt |
|
|
|
|
|
|
|
мальному: a |
= V 2 / . |
|
|
|
|
|
|
||
n |
|
|
|
|
|
|
|
|
|
3. Равномерное прямолинейное движение точки. В этом случае |
|||||||||
|
|
|
|
|
|
|
an = 0, |
a = 0 . |
|
Из рассмотренных случаев видно, что касательное ускорение характеризует изменение величины (модуля) скорости, а нормальное – изменение направления скорости.
4. Равнопеременное движение. За равные промежутки времени скорости изменяются на равные величины:
|
|
a |
= |
dV |
|
= const, |
dV = a dt, |
|
|
|||
dt |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
V |
|
t |
|
|
|
|
|
|
|
|
|
|
т |
dV = т a dt |
|
|
|||||
|
|
|
|
V0 |
0 |
|
|
|
|
|
||
или V -V0 = a t Ю V = V0 + a t, где V0 |
– скорость точки при t = 0 (на- |
|||||||||||
чальная скорость). |
|
|
|
|
|
|
|
|
|
|
||
Так как |
|
|
|
|
|
|
|
|
|
|
||
V = |
dS |
, Ю dS = Vdt |
или |
dS = (V + a t)dt, |
||||||||
|
||||||||||||
|
dt |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
интегрируя, получим |
|
|
|
|
|
|
|
|
|
|
||
S |
t |
|
|
|
|
a t |
2 |
|
||||
т dS = т(V0 + a t)dt, |
S = V0t + |
|
. |
|||||||||
|
|
|||||||||||
0 |
|
0 |
|
|
|
|
|
2 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
43 |
|
|
|
|
|

Л е к ц и я 5
ПРОСТЕЙШИЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
Поступательное движение твердого тела. Теорема о траекториях, скоростях и ускорениях точек твердого тела при поступательном движении. Вращательное движение твердого тела вокруг неподвижной оси. Угловая скорость и угловое ускорение. Траектории, скорости и ускорения точек вращающегося твердого тела. Равномерное и равнопеременное вращение твердого тела.
Поступательное движение твердого тела
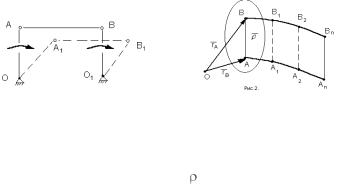
Поступательным движением твердого тела называется такое движение, при котором отрезок прямой, соединяющий две любые точки тела, во все время движения остается себе параллельным (например, АВ, рис. 1).
Теорема. При поступательном движении твердого тела траектории, скорости и ускорения всех его точек одинаковы.
Д о к а з а т е л ь с т в о. Пусть отрезок AB тела за время t перемещается поступательно. Возьмем произвольную точку O и опреде-
лим в |
пространстве положение |
отрезка AB радиусами-векторами |
|
rA и rB |
(рис. 2). Обозначим |
– |
радиус-вектор, определяющий поло- |
жение точки В относительно точки |
А. |
Вектор не изменяется ни по |
величине, ни по направлению, так |
как AB = const (по определению поступательного движения). Из соотношения (*) видно, что траектория точки В получается из траектории
точки А параллельным смещением точек этой траектории на постоян-
ный вектор = AB . Таким образом, траектории точек А и В будут одинаковыми.
44
|
|
|
Рис. 1 |
Рис. 2 |
|
rB = rA + . |
(*) |
|
Возьмем производную по времени от равенства (*). Тогда
|
dr |
dr |
|
|
|
|
||||
|
B |
= |
|
A |
, т.е. V |
= V |
|
, |
||
|
|
|
|
|
||||||
|
dt |
|
dt |
B |
A |
|
||||
|
|
|
|
|
|
|||||
dV |
|
dV |
|
|
|
|
||||
|
B |
= |
|
A |
или a |
= a |
|
. |
||
|
|
|
A |
|||||||
|
dt |
|
dt |
B |
|
|
||||
|
|
|
|
|
|
|||||
Следовательно, при поступательном движении твердого тела скорости и ускорения всех его точек в данный момент времени одинаковы.
Очевидно, что для изучения поступательного движения тела достаточно изучить движение какой-либо одной точки. То есть задача сводится к задаче кинематики точки, рассмотренной нами в предыдущей лекции.
Отметим, что сам факт поступательного движения не определяет ни закона движения, ни вида траектории. При поступательном движении точки тела могут описывать любые траектории (например, окружности – см. рис.1). Но все они будут одинаковы.
Вращение твердого тела вокруг неподвижной оси
Если во все время движения твердого тела две какие-либо его точки остаются неподвижными, то такое движение тела называется вращением вокруг неподвижной оси, а прямая, проходящая через две неподвижные точки, называется осью вращения тела. При таком движении тела все его точки, не лежащие на оси вращения, будут опи-
45
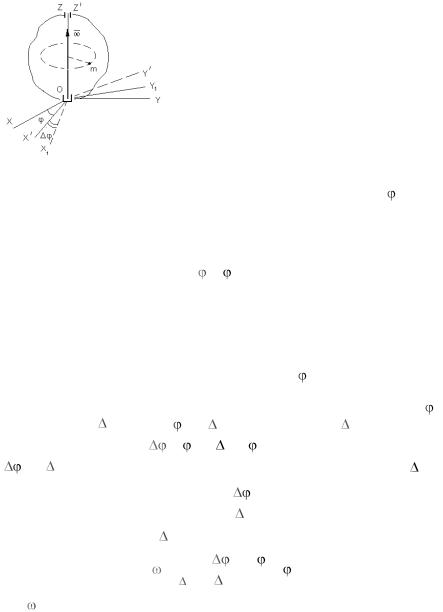
сывать окружности с центром на оси вращения и с плоскостями, перпендикулярными к ней.
Выберем неподвижную систему координат ОXYZ, ось OZ которой совпадает с осью вращения твердого тела. Возьмем также систему OX ўY ўZ ў , вращающуюся вместе с телом (рис. 3). Положение подвижной системы относительно неподвижной будет определяться двугранным
Рис. 3 углом между плоскостями с XOZ и X1OZ1 . Обозначим его через . Угол 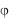
изменяется с течением времени и представляет собой некоторую непрерывную функцию времени t. Таким образом, закон вращательного движения твердого тела имеет вид
= (t) .
За положительное направление  примем направление против часовой стрелки, если смотреть со стороны положительного направления оси OZ .
примем направление против часовой стрелки, если смотреть со стороны положительного направления оси OZ .
Угловая скорость |
|
||
Для характеристики быстроты изменения |
введем понятие угло- |
||
вой скорости. |
|
|
|
Пусть в момент времени t положение тела определялось углом (t), |
|||
а в момент t + t – углом |
(t + |
t) . Тогда за время t угол поворота |
|
получит приращение |
= (t + |
t) - (t) . |
Отношение приращения |
к t называется средней угловой скоростью тела за время t:
ωcp = |
|
|
. |
|
||
|
|
|
||||
|
|
t |
|
|||
Переходя к пределу при t ® 0 , получим |
|
|||||
= lim |
|
= |
d |
= , |
||
t |
dt |
|||||
t ®0 |
|
|
||||
где – угловая скорость тела в данный момент времени.
46

Величина угловой скорости твердого тела при вращении его вокруг неподвижной оси равна первой производной от угла поворота по вре-
мени. |
|
Знак |
определяет направление вращения тела. Если вращение |
происходит против хода часовой стрелки, то > 0, т.е. положительное приращение угла отсчитывается против хода часовой стрелки. Едини-
ца измерения угловой скорости 1/c или c-1 . |
, модуль |
||
Угловую скорость можно изображать в виде вектора |
|||
которого равен |
|
и который направлен вдоль оси вращения в ту сто- |
|
|
|
|
|
рону, откуда вращение видно происходящим против хода часовой стрелки.
Угловое ускорение
Угловое ускорение характеризует изменение угловой скорости с
изменением времени. |
|
|
|
|
|
|
|
|
|
|
|
Если за промежуток времени |
t |
= t1 - t0 |
угловая скорость изменит- |
||||||||
ся на величину = |
1 - |
0 , то числовое значение среднего углового |
|||||||||
ускорения равно: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
εcp = |
|
|
|
. |
|
|
||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
t |
|
|||
Переходя к пределу при |
t ® 0 , получим |
|
|||||||||
ε = |
lim |
|
ω |
= |
dω |
= |
d 2 |
|
= = . |
||
|
|
|
|
||||||||
|
t ®0 t |
dt |
|
|
dt2 |
|
|||||
Числовое значение углового ускорения тела в данный момент времени равно первой производной от угловой скорости или второй производной от угла поворота по времени.
Единица измерения углового ускорения 1/c2 или c-2 . |
||
|
|
|
dω |
|
|
Вектор углового ускорения ε = |
|
направлен вдоль оси вращения: |
dt |
||
|
|
то вращение ускоренное, если |
если ε совпадает с направлением |
ω , |
|
нет – замедленное.
47

Равномерное и равнопеременное вращение
Если угловая скорость во все время движения тела остается посто-
янной, то вращение тела называется равномерным ( |
= const). |
||
Закон движения в дифференциальной форме имеет вид |
|||
|
d |
= ωdt . |
|
В начальный момент |
времени t = t0 угол |
= 0 . Интегрируя |
|
уравнение в пределах |
0 и 0 t , получим |
|
|
|
= |
0 + ωt . |
|
При 0 = 0 = ωt |
или = |
|
. |
|
|||
|
|
t |
|
В технике угловая скорость соответствует характеристике, называемой частотой вращения, обозначаемой как n и измеряемой в об/мин.
Так как 1 оборот = 2 радиан, 1 мин = 60 с, то перевод из об/мин в c-1 осуществляется по формуле
= 260n = 30n .
Если угловое ускорение все время остается постоянным, то такое вращение называется равнопеременным (ε = const):
|
|
ε = |
dω |
Ю dω = εdt . |
|
|
|||||
|
|
dt |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||
Проинтегрировав в пределах ω0 ω и 0 t , получим ω = ω0 + εt . |
|||||||||||
Представив ω = |
d |
, получим |
|
|
|
|
|
|
|||
dt |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
= ω |
+ εt |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
dt |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
или |
|
|
|
|
|
|
|
|
|
|
|
|
d |
= ω dt + εtdt Ю |
|
|
+ ω t + |
εt2 |
|||||
|
= |
0 |
|
. |
|||||||
|
|
||||||||||
|
|
0 |
|
|
|
|
|
0 |
2 |
|
|
Если 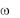 и
и 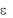 имеют одинаковые знаки, то движение является равно-
имеют одинаковые знаки, то движение является равно-
ускоренным, в противном случае – равнозамедленным.
48
СКОРОСТИ И УСКОРЕНИЯ ТОЧЕК ВРАЩАЮЩЕГОСЯ ТЕЛА
Скорости точек тела
Возьмем точку М тела на расстоянии h от оси вращения (рис. 4). Точка M будет описывать окружность радиуса h, плоскость которой перпендикулярна к оси вращения. Если за время dt происходит эле-
|
|
|
|
dS |
|
|
ментарный поворот d , то V |
= |
|
, ско- |
|||
dt |
||||||
|
|
|
|
|
||
рость V |
называется линейной или окруж- |
|||||
ной. |
Учитывая, что dS = hd |
, |
получим |
|||
|
hd |
= h . |
|
|
|
|
V = |
|
|
|
|
||
dt |
|
|
|
|||
|
|
|
|
|
||
Числовое значение скорости точки вращающегося тела равно произведению угловой скорости тела на расстояние от
этой точки до оси вращения. Скорость направлена по касательной к
описываемой окружности. Так как для всех точек тела одинаковы, то скорости точек вращающегося тела пропорциональны их расстояниям до оси вращения (рис. 5).
Рис. 5
Для определения ускорений точек тела воспользуемся формулами
a = |
dV |
, |
a = |
V 2 |
|||
|
|
|
. |
||||
|
|
|
|||||
|
dt |
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
В нашем случае |
|
|
|
|
|
|
|
= h Ю a |
= |
hd |
|
Ю , |
|||
dt |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
49 |
|
|
|
|
a = h , an = h2h 2 = 2h,
a = 
 a2 + an2 =
a2 + an2 = 
 (h )2 + ( 2h)2 = h
(h )2 + ( 2h)2 = h
 2 + 4 .
2 + 4 .
Отклонение вектора полного ускорения от радиуса определяется углом (рис. 6):
a
tg = an = 2 .
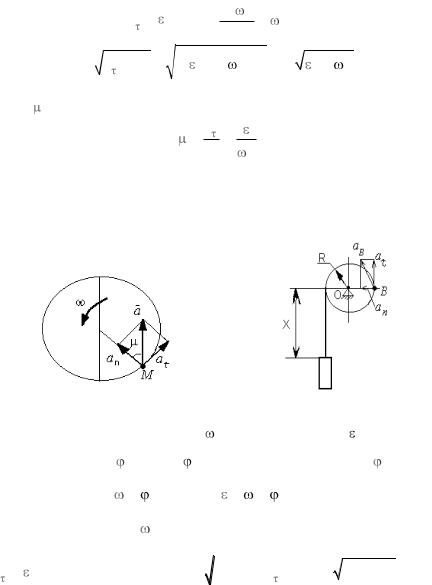
Задача. Вал радиуса R =10 см приводится во вращение гирей, подвешенной к нему на нити (рис. 7). Движение гири выражается уравнением x = 100t2, где х – расстояние гири от места схода нити с поверхности вала, выражаемое в сантиметрах; t – время в секундах.
|
|
|
Рис. 6 |
|
|
|
|
|
Рис. 7 |
|
|
||
|
|
|
|||||||||||
|
Определить угловую скорость |
и угловое ускорение вала, а также |
|||||||||||
полное ускорение точки В на поверхности вала в момент времени t. |
|||||||||||||
|
Решение. |
х = R |
, |
где |
– |
угол |
поворота |
вала |
= х / R = |
||||
= |
100t2 |
= 10t2 |
рад , |
= = 20t |
с-1, |
= |
= = 20 с-2 , |
|
|
||||
|
|
|
|||||||||||
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
= |
2R = 400t210 = 4000t2 см/с, |
|
|
|
|
||||
|
|
|
п |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
(aп )2 + (a )2 = 200 |
|
|
|
||||||||
a |
= R = 20 Ч10 = 200 см/с2, aB = |
1 + 400t4 см/с2. |
|||||||||||
|
|
|
|
|
|
50 |
|
|
|
|
|
|
|
