vср =
Глава 6.
Дифференциальное исчисление функции одной переменной
§ 6.1. Производная и дифференциал
6.1.1.Вычисление скорости прямолинейного движения
Процесс движения точки вдоль прямой называется прямолинейным движением точки и определяется законом движения S = ϕ(t), указывающим координату S на числовой оси в момент времени t. Согласно этому закону за каждый определенный промежуток времени t = t −t0 , отсчитываемый от момента времени t0 , точка проходит расстояние S = ϕ(t) −ϕ(t0 ) = ϕ(t + t) −ϕ(t0 ) со средней скоростью
S
t
Чем меньше временной промежуток t, тем точнее измеряется средняя скорость перемещения S за время t. Принято считать, что в процессе уменьшения интервала t мы будем получать значение средних скоростей в момент времени t0 . Таким образом, мы приходим к понятию истинной скорости в момент времени t0 , определяемой пределом
lim |
ϕ(t0 + |
t) −ϕ(t0) |
= lim |
S |
= v(t0 ). |
|
|
t→0 |
t |
t→0 |
t |
Заметим, что если этот предел не существует, то величина скорости в момент времени t0 не определена.
. Найти скорость в момент времени t = 1.
ПРИМЕР 6.1.1.
1. Закон движения задается зависимостью координаты x от времени t x = gt2
2
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(t + t)2 |
|
|
t2 |
|
|
|
|
g t2 |
Имеем x = x(t + |
t) −x(t) = g |
|
|
|
−g |
|
|
= gt |
t + |
|
, |
2 |
|
|
2 |
2 |
( ) = t→0 |
x |
= |
t→0 |
|
|
+ |
|
|
t |
|
= |
|
. |
|
|
t |
|
|
2 |
|
|
|
v t |
lim |
|
|
lim |
gt |
|
g |
|
|
|
gt |
|
|
|
При t = 1 получаем v(1) = g.
2. Закон движения задается зависимостью
1 x(t) = (t −t0 ) sin t −t0
Найти скорость в момент времени t = t0
Вначале заметим, что функция x(t) при t = t0 имеет устранимый разрыв и становится непрерывной, если ее доопределить значением x(t0 ) = 0 (см. устранимый разрыв в п 5.3.7). Учитывая это, находим
x = x(t0 + |
t) −x(t0) = |
t ·sin |
1 |
. |
|
t |
Поэтому предел |
|
|
|
|
|
|
lim |
x |
= lim sin |
1 |
|
|
|
|
t |
|
|
t→0 |
t t→0 |
|
|
не существует (см. пример 5.3.5).
Таким образом, точка, выполняющая прямолинейное движение по заданному закону x(t) в момент времени t = t0 истинной скорости не имеет.
6.1.2. Понятие производной
Представление о процессах, происходящих в окружающем мире, связано с понятием скорости изменения тех или иных величин. Мы рассмотрели простейший процесс — прямолинейное движение точки. В других процессах указан закон y = f (x) изменения величины y в зависимости от аргумента x и понятие «скорости» изменения y относительно x приводит к вычислению предела отношения приращения функции f = f (x + x) − f (x) к приращению аргумента x.
Определение 6.1.1 (производной). Если существует предел отношения приращения функции f (x) в точке x к приращению независимого аргумента x, то он называется производной функции f (x) по переменной x и обозначается f ′(x)
lim |
f (x + |
x) |
− f (x) |
= lim |
f |
= f ′(x). |
|
x |
|
|
x→0 |
|
x→0 |
x |

Приняты различные способы обозначения производной: f ′(x), d f , y′(x), dx
fx′ и др.
Операция нахождения производной называется дифференцированием функции. Если f ′(x) существует во всех точках интервала (a, b), то говорят, что f (x) имеет производную f ′(x) на (a, b) или f (x) дифференцируема на
(a, b).
6.1.3.Вычисление производной основных элементарных функций y = ax + c,
y = sin x, y = loga x
1. Для ax + b находим |
y = a(x + |
|
|
x) + c −(ax + c) = a x, |
|
|
|
|
|
|
|
|
|
|
|
|
y′ = lim |
|
|
|
y |
= lim |
a |
x |
= a. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→0 |
|
x |
|
|
|
x→0 |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
В частности, для постоянной функции y = C — const приращения |
y = 0 |
при любых |
x , поэтому |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(C)′ = 0, |
(C — const). |
|
|
|
|
|
|
|
|
|
|
2. Для y = sin x приращение |
|
y = sin(x + |
|
x) − sin x представим в виде |
|
x) −sin x = 2 cos x + |
|
x |
sin |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin(x + |
|
|
|
|
. Тогда, используя первый замеча- |
2 |
|
2 |
тельный предел, получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
+ |
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→0 |
x |
x→0 |
2 |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
lim cos |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= x→0 |
|
x |
+ |
x→0 |
|
2 |
|
= |
cos x |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim cos |
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
Таким образом, |
|
|
|
|
(sin x)′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= cos x. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
УПРАЖНЕНИЕ 6.1.1. Получить аналогичным образом формулу (cos x)′ |
= |
−sin x. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. |
Для |
y = loga x |
преобразуем |
y |
|
= loga(x + |
x) − loga x |
|
= |
|
= loga |
1 + |
x |
|
. Используя второй замечательный предел, находим |
|
x |
|
|
|
|
|
|
|
|
|
|
|
loga 1 + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
y |
= lim |
1 |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→0 x |
x→0 x |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim log |
|
|
|
1 |
|
|
x |
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= x |
|
|
|
+ x |
|
|
= x loga |
= x ln a . |
|
Таким образом |
|
|
|
|
|
|
|
|
x→0 |
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(log |
x)′ |
= |
|
log |
|
|
e = |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
x ln a |
|
|
|
|
|
|
|
|
|
|
|
|
|
В частности, для натурального логарифма при a = e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(ln x)′ |
|
= |
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6.1.4. Дифференциал функции |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
По теореме о необходимом и достаточном условии существования пре- |
|
дела мы имеем два эквивалентных условия |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
f |
= f |
′(x) |
|
|
|
|
|
|
f |
= f ′(x) + α( |
x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→0 |
x |
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
→ 0. Обозначим |
|
где α( |
|
x) — бесконечно малая функция от x при |
|
|
|
α( |
x) |
x = o( |
x) и напомним, что o-малое от |
x обозначает свойство |
|
o( |
x) |
→ 0 при |
x → 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Учитывая сказанное, запишем условие существования f ′(x) в виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f = f ′(x) |
x + o( |
x). |
|
|
|
|
|
|
|
(6.1.1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
o( |
x) |
= 0. |
|
|
|
|
|
|
|
|
|
|
|
(6.1.2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→0 |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, нами доказано следующее утверждение
Теорема 6.1.1. (о необходимом и достаточном условии дифференцируемости). Функция f (x) дифференцируема в точке x тогда и только тогда, когда ее приращение представляется в виде (6.1.1) и в этом представлении выполняется условие (6.1.2).
Обратим внимание на то, что: 1) в представлении (6.1.1) выражение f ′(x) x является линейной функцией по x в фиксированной точке x; 2) бесконечно малая функция o( x) имеет более высокий порядок малости, чем x. В силу этих двух свойств представления (6.1.1) выражение f ′(x) dx называют линейной частью приращения f . Поэтому существует другое определение дифференцируемости.
Определение 6.1.2 (дифференцируемости). Функция f (x) называется дифференцируемой в точке x, если ее приращение f в этой точке имеет главную линейную часть, т. е. представляется в виде
f = A(x) x + o( x), где lim |
o( |
x) |
= 0. |
|
|
x→0 |
x |
При этом величина A(x) = f ′(x) называется производной функции f (x) в точке x, а главная линейная часть f ′(x) x называется дифференциалом и обозначается
df = f ′(x) dx.
6.1.5.Геометрический смысл производной и дифференциала
В декартовой системе координат Oxy изобразим график функции y = f (x). Две
точки M0 (x0 , f (x0 )) и M1 (x1 , f (x1 )) этого графика соединим отрезком прямой, ко-
торую назовем секущей, рис. 6.1.
y |
|
|
|
|
f (x1 ) |
|
M1 |
|
|
|
|
|
|
|
M0 |
|
|
y |
f (x0 ) |
|
|
|
|
|
|
|
O |
α |
x |
|
|
|
|
|
|
|
|
|
|
x0 |
|
x1 |
x |
|
|
|
|
Рис. 6.1 |
|
|
Уравнение этой секущей ищем в виде y = kx + b. Учитывая, что угловой
коэффициент k = tg α = f , запишем уравнение секущей в виде y = f x + b. x x
Так как эта прямая проходит через точку (x0 , f (x0 )), то выполняется условие
f (x0 ) = |
f |
+ b, |
|
|
x0 |
|
x |
|
откуда находим коэффициент b = f (x0 ) − |
|
f |
. Подставляя найденное зна- |
|
|
x0 |
|
x |
чение b в искомое уравнение секущей y = |
f |
+ b и выполняя группировку, |
|
получаем уравнение секущей в виде |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
|
y − f (x0) = |
|
|
(x −x0 ). |
|
|
x |
|
Устремим теперь точку M1 к точке M0 . Тогда приращение |
|
и если существует предел |
|
|
|
|
|
|
lim |
f |
|
= f ′(x0 ), |
|
x |
|
x→x0 |
|
|
|
то одновременно выполняются два условия:
(6.1.3)
x = x −x0 → 0
(6.1.4)
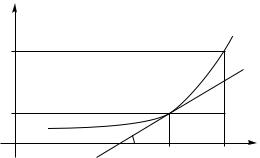
1)секущая M1 M0 стремится при M1 → M0 занять предельное положение, которое мы назовем касательной в точке (x0 , f (x0 )) к графику функции f (x);
2)угловой коэффициент касательной в точке (x0 , f (x0 )) равен f ′(x0 ), а само уравнение касательной получается из уравнения (6.1.3) предельным переходом в правой части при x = x1 −x0 → 0 и принимает вид
y |
|
y − f (x0) = f ′(x0 )(x −x0) |
(6.1.5) |
|
|
|
|
|
|
f (x0 + |
x) |
|
C |
y = f (x) |
|
|
|
|
|
|
|
|
B |
|
y − f (x0) = f ′(x0 )(x −x0 ) |
|
f (x0 ) |
|
M0 |
A |
|
|
|
O |
|
α0 |
|
|
|
|
|
|
x0 |
x0 + |
x |
x |
|
|
|
|
|
|
|
|
Рис. 6.2 |
|
|
|
Вывод 1 (геометрический смысл производной). Производная f ′(x0 ) в
точке x0 есть угловой коэффициент касательной в этой точке, т. е. равна тангенсу угла наклона касательной к оси Ox, (рис. 6.2)
f ′(x0 ) = k0 = tg α0 .
Вернемся к уравнению касательной (6.1.5) и заметим, что приращение зависимой переменной линейной функции, определяемой (6.1.5) и соответствующей приращению независимого аргумента x равно дифференциалу функции, вычисленному в точке касания x0 :
Вывод 2 (геометрический смысл дифференциала). Дифференциал d f = f ′(x0 ) x, вычисленный при заданных x0 и x, равен приращению y координаты y уравнения касательной, проведенной к графику y = f (x) в
точке (x0 , f (x0 )).
На рис. 6.2 величина дифференциала d f обозначается отрезком AB. Отрезок AC равен приращению функции f , а отрезок BC представляет бесконечно малую более высокого порядка малости o( x) = BC. В этих обозначениях формула приращения функции (6.1.1) принимает вид AC = AB + BC. Геометрический смысл формулы приближенного вычисления (6.1.1) состоит в том, что мы пренебрегаем величиной отрезка BC (при достаточно малых значениях x!) и считаем, что приближенно выполняется равенство f (x0 + x) ≈ f (x0 ) + AB (рис. 6.2).

ЗАМЕЧАНИЕ 6.1.1. На рис. 6.1 и рис. 6.2 мы ограничились изображением случая x = x1 −x0 > 0, полагая, что существование предела (6.1.4) соответствует совпадению левого предела при x = x1 −x0 < 0 и правого предела при x > 0, когда x → 0. Может случится, что в точке x0 существуют левый
и правый пределы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
f |
|
= f |
′(x |
|
− |
0), |
|
lim |
f |
= f ′(x |
+ 0), |
x |
0 |
x |
0 |
x |
|
→ |
x0 |
− |
|
|
|
|
→ |
x0 +0 |
x |
0 |
|
|
|
|
|
f ′(x0 |
− |
|
6 |
|
|
|
|
|
не равные между собой: |
|
|
|
0) = f ′(x0 + 0). Тогда говорят, что в точ- |
ке x0 существуют левая и правая производные, не равные друг другу. Это означает, что в точке x0 существуют
|
y |
|
|
левая касательная с угловым коэффици- |
|
|
|
|
ентом k1 = = tg α1 = f ′(x0 −0) и правая |
|
|
α2 |
касательная с угловым коэффициентом |
O |
|
α1 |
k2 = tg α2 = f ′(x0 + 0) (рис. 6.3). |
|
|
|
|
x |
|
|
|
x0 |
|
|
|
Рис. 6.3 |
УПРАЖНЕНИЕ 6.1.2. Показать, что функция |
|
|
sin x, при x 6 0 |
|
|
f (x) = ( x sin 1 , при x > 0 |
|
|
x |
|
|
|
|
в точке x0 = 0 имеет левую производную и левую касательную и не имеет правой производной и правой касательной.
6.1.6. Непрерывность и дифференцируемость
Функция f (x), дифференцируемая в точке x0 , будет в этой точке непрерывной. Это следует из формулы для приращений (6.1.2) для дифференцируемой функции. Действительно, согласно этой формуле и свойству абсо-
лютных величин, имеем неравенство |
|
|
|
| |
|
f |
| |
6 |
| |
f |
′(x ) x |
+ |
| |
x |
| |
|o( x)| |
= |
|
|
|
|
|
|
|
0 |
|| |
|
| |
|
|
| x| |
= | x| |
|f ′(x0 )|+ | |
|( x|)| |
6 | x|C, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
o x |
|
где |
| |
f |
′(x0 ) + |o( |
x)| |
6 C — const. |
|
|
|
|
|
|
|
|
|
| |
| |
x |
| |
|
|
|
|
|
|
|
|
|
Согласно этому неравенству для любого ε > 0 достаточно взять δ < ε ,
C
тогда будет
| x| < δ = | f | < C,
что означает непрерывность в точке x0 .
Обратное утверждение в общем случае не верно. Функция, непрерывная в точке x0 может в этой точке не иметь производной. Рассмотрим два примера.
ПРИМЕР 6.1.2. y = x |
|
x0 |
| |
= |
x −x0 , при x > x0 , |
Здесь y′(x0 + 0) = |
1 = |
1 = y′(x0 |
− |
0). |
| − |
|
|
−(x −x0 ), при x < x0 . |
|
6 − |
|
|
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
, при x 6= 0, |
|
ПРИМЕР 6.1.3. y = |
x sin |
|
|
x |
|
|
|
|
|
|
|
|
|
0, при x = 0. |
|
В этом примере при x = 0 не существует ни левая, ни правая производная, хотя эта функция непрерывная в точке x = 0.
Не имеет производной при x = 0 функция f (x) из упражнения 6.1.2 предыдущего пункта. Для нее f ′(x0 −0) = cos 0 = 1, а f ′(0 + 0) не определена.
§6.2. Свойства операции дифференцирования
Множество элементарных функций определялось в п 0.6.4 вводится как результат арифметических операций ±, ×, div, а также взятия обратной функции f −1 и композиции двух и более функций f ◦g ◦. . . ◦ϕ совершаемых в начале над тремя основными функциями ax + b, sin x, loga x, а затем над уже полученными функциями. Поэтому, чтобы выполнить дифференцирование произвольной элементарной функции, надо вывести правила дифференцирования исходных основных элементарных функций и указанных выше операций. Производные трех основных элементарных функций мы вычислили в п 6.1.3. В этом параграфе мы научимся дифференцировать указанные выше три типа операций.
6.2.1.Дифференцирование арифметических операций
Теорема 6.2.1. (арифметические свойства производной). Пусть функции f (x) и g(x) дифференцируемы в точке x, тогда
a) их сумма и разность дифференцируемы в x, причем
(f (x) ±g(x))′ = f ′(x) ±g′(x);
b)их произведение дифференцируемо в точке x, причем
( f (x)g(x))′ = f ′(x)g(x) + f (x)g′(x),
( f (x) ±g(x))′ = lim
вчастности (C f (x))′ = C f ′(x), если C —const;
c)их частное дифференцируемо в x, и, если g(x) 6= 0, то
(x) ′ = f (x)′g(x) − f (x)g′(x) . (x) g2 (x)
ДОКАЗАТЕЛЬСТВО. a) используя определение производной и свойство предела суммы, запишем
f (x + x) ±g(x + x) −( f (x) ±g(x)) =
x→0 |
x |
f |
|
|
g |
|
|
|
|
= lim |
± |
lim |
= f ′(x) |
± |
g′(x); |
|
x |
|
|
x→0 |
x→0 |
x |
|
b) для доказательства этого свойства запишем f (x + x) = f (x) + f , |
g(x + x) = g(x) + g. Тогда, по определению производной, с учетом арифметических свойств предела, находим
( f g)′(x) = lim |
f (x + |
x)g(x + |
|
x) − f (x)g(x) |
= |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
x→0 |
|
|
|
|
|
|
|
|
|
|
= lim |
( f (x) + |
f )(g(x) + |
g) − f (x)g(x) |
= |
|
|
|
x |
|
x→0 |
f |
|
|
g |
|
|
f |
|
|
= lim |
|
g(x) + lim f (x) |
|
+ lim |
g = |
|
|
|
|
|
|
x→0 x |
x→0 |
x |
x→0 x |
|
|
|
|
|
|
= f ′(x)g(x) + f (x)g′(x) + f ′(x) lim g. |
|
|
|
|
|
|
|
|
|
|
|
|
|
x→0 |
Приращение дифференцируемой функции |
g является бесконечно ма- |
лой функцией, см. п 6.1.6, поэтому |
g → 0 при |
x → 0 и мы получаем требу- |
емое правило b). Правило (C f (x))′ |
= C f ′(x) следует отсюда, если g(x) = C — |
const, так как C′ = 0; |
|
|
|
|
|
|
|
|
|
|
|
c) вначале преобразуем отношение приращения функции f (x)/g(x) к приращению аргумента x, предварительно заметив, что из дифференцируемости g(x) в точке x следует непрерывность g(x) и то, что g(x) =6 0 влечет это свойство g(x + x) =6 0 в некоторой окрестности x, поэтому определено
частное |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x + x) |
− |
f (x) |
|
|
f (x) + |
f |
− |
f (x) |
f |
g |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
g(x) − f (x) |
|
|
|
|
|
|
g(x + x) |
g(x) |
g(x) + |
g |
g(x) |
|
|
|
|
|
|
= |
|
|
= |
|
x |
|
x |
. |
|
|
x |
|
|
|
|
|
x |
|
|
|
|
g2 (x) + g(x) g |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Теперь, учитывая, что |
g → 0 при |
x → 0, и используя арифметические |
свойства предела, заключаем, что левая часть этих равенств стремится по
определению производной к величине |
f (x) |
|
′ |
|
, а правая часть — к величине |
g(x) |
f ′g −g′ f |
. Правило c), а вместе с ним и теорема 6.2.1 доказаны. |
g2 |
|
|
|
|
210
Следствие 6.2.1. Пусть f (x) = C1 f1 (x) + C2 f2(x) + ...+ +Cn fn(x), где C1 ,
C2 , . . . , Cn — const и все функции f1 (x), f2 (x), . . . , fn(x) дифференцируемы,
тогда
f ′(x) = C1 f1′(x) + . . . + Cn fn′(x).
Это следует из многократного применения свойств a) и b) теоремы 6.2.1.
Следствие 6.2.2. Если f (x) = u(x)v(x)w(x) и функции u(x), v(x), w(x) дифференцируемы, то, применяя правило b) дважды, получим
((uv)w)′ = (uv)′w + uvw′ = u′vw + uv′w + uvw′.
Аналогично дифференцируется произведение большего числа сомножителей.
Следствие 6.2.3. Пусть f (x) и g(x) дифференцируемы в точке x, тогда: a) определен дифференциал их суммы и разности:
d( f ±g) = d f ±g; b) определен дифференциал их произведения d( f g) = g d f + f dg,
в частности при g = C — const d(C f ) = C d f ;
c) определен дифференциал их частного и, если g(x) 6= 0, то |
g |
|
|
g2 |
d |
f |
|
= |
g d f − f dg |
. |
|
|
|
Проверка этих свойств основана на связи между дифференциалом и производной функции f (x) = f ′ dx:
a) d( f ±g) = (g ±g)′dx = f ′ dx ±g′ dx = d f ±dg;
b) d( f g) = ( f g)′dx = ( f ′ dx)g + f (g′ dx) = g d f + f dg, в частности если
g = C — const, то dg = C′ dx = 0 и мы получаем d(C f ) = C d f ; |
g |
|
g |
|
′ |
|
g2 |
|
g2 |
c) d |
f |
= |
|
f |
|
dx = |
( f ′ dx)g − f (g′ dx) |
= |
g d f − f dg |
. |
|
|
|
|
|
|
|
Теорема 6.2.1 позволяет расширить список функций, которые мы уже умеем дифференцировать. Рассмотрим примеры.
ПРИМЕР 6.2.1.
1. Вычислим (tg x)′.
Так как (sin x)′ = cos x, а (cos x)′ = −sin x, см. п 6.1.3, то согласно правилу
c) теоремы 6.2.1 находим |
|
|
|
|
|
|
|
|
|
|
|
|
|
sin x |
|
′ |
( |
sin x |
)′ |
cos x |
|
sin x cos x |
)′ |
|
|
|
|
|
|
(tg x) = |
|
|
= |
|
|
− |
( |
= |
|
|
|
|
|
cos x |
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
cos2 x |
|
|
cos2 x + sin2 x |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
cos2 x |
cos2 x |









