
Высшая_математика_Том1
.pdf
ПРИМЕР 3.4.3. Найти точку B, симметричную точке A(4, −3, 1) относительно плоскости x + 2y −z −3 = 0.
РЕШЕНИЕ. Точки A и B должны лежать на одной прямой, перпендикулярной плоскости, и одинаково отстоять от этой плоскости. Найдём уравнение прямой, проходящей через точку A и перпендикулярной плоскости
x −4 |
= |
y + 3 |
= |
z −1 |
. |
1 |
|
|
|||
2 |
|
−1 |
|||
Найдём точку пересечения этой прямой и плоскости: x = = 4 + t, y = −3 + 2t, z = 1 −t подставим в уравнение плоскости (4 + t) + 2(−3 + 2t) − (1 −t) −3 = 0; отсюда t = 1. Значит, точка пересеченияC(5, −1, 0). Она делит отрезок AB пополам. Но координаты середины отрезка равны полусумме
координат крайних точек. Значит, |
|
|
|
|
||||
xC = |
xA + xB |
, |
yC = |
yA + yB |
, |
zC = |
zA + zB |
. |
|
|
|
||||||
2 |
|
2 |
|
2 |
|
|||
Отсюда
xB = 2xC −xA = 6, yB = 2yC −yA = 1,
zB = 2zC −zA = −1.
Симметричная точка B(6, 1, −1) найдена.
3.4.6.Уравнение плоскости, проходящей через данную точку перпендикулярно заданной прямой
Очевидно, нормальным вектором к искомой плоскости может служить направляющий вектор прямой s = {l, m, n}. Применяя формулу (3.3.1), получаем уравнение искомой плоскости
l(x −x0 ) + m(y −y0) + n(z −z0) = 0.
ПРИМЕР 3.4.4. Найти расстояние точки A(7, 9, 7) от прямой
x −2 |
= |
y −1 |
= |
z |
. |
4 |
|
|
|||
3 |
2 |
||||
РЕШЕНИЕ. Запишем уравнение плоскости, проходящей через точку A перпендикулярно прямой:
4(x −7) + 3(y −3) + 2(z −7) = 0
или
4x + 3y + 2z −69 = 0.
Найдём точку пересечения прямой и плоскости B(10, 7, 4). Искомое рассто-
яние от точки A до прямой
q √
AB = (10 −7)2 + (7 −9)2 + (4 −7)2 = 22.
141

3.4.7.Угол между прямой и плоскостью. Условие перпендикулярности и параллельности прямой и плоскости
Пусть даны прямая L: x −x0 = y −y0 = z −z0 и плоскость P : Ax + By +
Cz + D = 0. |
|
|
|
l |
m |
n |
|||
|
|
|
|
|
|
||||
|
|
|
n |
|
|
|
L |
Угол между прямой и плоскостью — |
|
|
|
|
|
s |
это угол между прямой и проекцией пря- |
||||
|
|
|
|
|
|||||
|
|
|
|
|
|
||||
|
|
|
ψ |
ϕ |
|
|
|
мой на плоскость. Обозначим искомый |
|
|
|
|
|
|
|
|
угол ϕ. Пусть ψ — угол между нормаль- |
||
|
|
|
|
|
|
|
|
||
|
|
|
ψ1 |
|
|
|
ным вектором плоскости n = {A, B,C} |
||
|
P |
|
|
|
|
|
|
и направляющим вектором прямой s = |
|
|
|
|
n1 |
|
|
|
|
{l, m, n}, если этот угол острый и ψ1 , если |
|
|
|
|
|
|
|
|
этот угол — тупой (рис. 3.12). |
||
|
|
Рис. 3.12 |
π |
|
−ψ|. Значит, по формуле приведения |
||||
|
Очевидно, ϕ = | |
|
|
||||||
|
2 |
|
|||||||
sin ϕ = sin |π2 −ψ| = |cos ψ|.
Но cos ψ = cos(ns) = |
n ·s |
. |
|
|
|
|
|
||
|n||s| |
|
|
|
|
|
||||
Получаем |
формулу для угла между прямой и плоскостью |
|
|||||||
b |
|
|
|Al + Bm + Cn| |
|
|
||||
|
sin ϕ = |
|
|
. |
(3.4.8) |
||||
|
|
|
|
|
|
||||
|
|
√A2 + B2 + C2 √l2 + m2 + n2 |
|||||||
|
|
|
|
|
|
||||
Прямая и плоскость перпендикулярны в том и только в том случае, если
векторы n и s коллинеарны. Отсюда |
|
|
|
|
|
|
|
|
A |
|
B |
C |
(3.4.9) |
||
L P |
|
= |
|
= |
|
. |
|
l |
m |
n |
|||||
Прямая и плоскость параллельны в том и только в том случае, если векторы n и s ортогональны, то есть n ·s = 0, или
L k P Al + Bm + Cn = 0. |
(3.4.10) |
3.4.8. Векторные уравнения прямой и плоскости
Рассмотренные выше уравнения прямых и плоскостей иногда называют уравнениями в координатной форме, так как они связывают координаты точек M(x, y) или M(x, y, z), лежащих на этих прямых и плоскостях. При этом легко заметить внешнюю схожесть или однотипность канонических уравнений прямых на плоскости и в пространстве, параметрических уравнений этих же прямых, общего уравнения прямой на плоскости и общего уравнения плоскости. Это объясняется тем, что при выводе таких уравнений
142

мы использовали одни и те же свойства векторных операций. Например, канонические уравнения прямых выводились из условия коллинеарности прямой и ее направляющего вектора; общее уравнение прямой на плоскости и общее уравнение плоскости — их ортогональность вектору нормали. Можно ожидать, что в векторной форме эти уравнения будут одинаковыми. Векторную форму записи уравнений особенно удобно использовать при рассмотрении многих теоретических вопросов.
Выберем в пространстве произвольную точку O, называемую полюсом. Положение точки M в пространстве однозначно определяется вектором OM, который называется радиус-вектором этой точки: при выбранном полюсе O, каждой точке M соответствует единственный вектор OM, связывающий полюс с этой точкой, и, наоборот — каждому радиус-вектору r = OM соответствует единственная точка M — конец радиус-вектора r. Радиус-вектор точки M будем обозначать r = r(M), а радиус-вектор точки M0 обозначаем
r0 = r(M0 ).
Векторное уравнение — это уравнение, связывающее радиус-вектор r произвольной точки точки M, радиус-векторы ri заданных точек Mi и, возможно, заданные векторы (a, s, n, N и т. п.).
Пусть в пространстве задана декартова прямоугольная система координат Oxyz, причём полюс совпадает с началом координат. Орт оси Ox обозначим i, оси Oy — j, оси Oz — k. Тем самым в пространстве задан декартов прямоугольный базис.
Положение точки в пространстве однозначно определяется ее тремя координатами. Следовательно, чтобы задать точку, нужно задать или все три ее координаты, или задать три уравнения, которые однозначно задавали бы эти координаты. Если задано лишь два уравнения, то, в общем случае, они не могут определить единственную точку в пространстве — им удовлетворяют координаты бесконечного множества точек, лежащих на некоторой линии. Аналогично если задано лишь одно уравнение, то ему удовлетворяют координаты точек, лежащих на некоторой поверхности (опять же, если исключить вырожденные случаи типа x2 + y2 + z2 = 0 или x2 + y2 + z2 + 1 = 0, которые, очевидно, не задают никакой поверхности).
Если задано векторное уравнение, то оно может определять единственную точку или линию или поверхность и в каждом случае вопрос о том, что определяет данное уравнение решается его анализом. Рассмотрим, например, уравнение r ·a = 0. По основному геометрическому свойству скалярного произведения ему удовлетворяют все радиус-векторы r, перпендикулярные вектору a. Таким образом, это уравнение на плоскости определяет прямую, проходящую через полюс (ведь радиус-вектор r = 0 удовлетворяет данному уравнению), перпендикулярно вектору a, а в пространстве оно определяет плоскость, также проходящую через полюс перпендикулярно
143
вектору a.
Аналогично, уравнение r ×a = 0 определяет геометрическое место точек, радиус-векторы которых параллельны вектору a, т. е. и на плоскости и в пространстве оно задает прямую, проходящую через полюс параллельно вектору a.
Таким образом, используя свойства операций над векторами, можно определить геометрический образ, соответствующий данному векторному уравнению. Важно уметь решать обратную задачу — составлять уравнение данного геометрического места точек.
Пусть символ M(r) (или r(M)) означает, что вектор r является радиусвектором точки M.
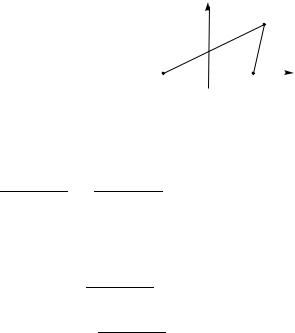
ПРИМЕР 3.4.5. Составить векторное уравнение плоскости, проходящей |
|||
через точку M0 (r0 ), параллельно неколлинеарным векторам p и q. |
|||
|
|
M |
РЕШЕНИЕ. Возьмем произвольную |
p |
|
точку M(r) в пространстве (рис. 3.13). Эта |
|
|
|
||
|
|
|
точка лежит на искомой плоскости тогда и |
M0 |
q |
|
только тогда, когда векторы M0 M = r −r0 , |
r0 |
|
|
p и q компланарны, а, значит, их смешан- |
r |
|
ное произведение равно нулю. Итак, ис- |
|
|
|
||
|
|
комое уравнение |
|
O |
|
|
|
|
|
(r −r0 ) ·p ·q = 0. |
|
|
Рис. 3.13 |
|
|
Легко получить векторное параметрическое уравнение данной плоско- |
|||
сти. Векторы p и q неколлинеарны и, следовательно, образуют базис на иско- |
|||
мой плоскости. Разлагая вектор M0 M = r −r0 , лежащий на той же плоскости |
|||
по базису p и q, получим уравнение искомой плоскости |
|||
|
|
|
r −r0 = t1 p + t2 q. |
Здесь t1 и t2 — параметры, т. е. произвольные действительные числа. |
|||
Аналогичными рассуждениями можно получить следующие векторные |
|||
уравнения прямых и плоскостей. |
|||
L.1) Параметрическое уравнение прямой, проходящей через точкуM0 (r0 ) |
|||
параллельно вектору s: |
|
|
|
|
r −r0 = ts. |
(3.4.11) |
L.2) |
Прямая проходит через точку M0 (r0 ) параллельно вектору s: |
|
|
(r −r0 ) ×s = 0. |
(3.4.12) |
L.3) |
Прямая, параллельная вектору s: |
|
|
r ×s = m. |
(3.4.13) |
L.4) Уравнение прямой, проходящей через две заданные точки M1 (r1 ) и
M2 (r2 ): |
(3.4.14) |
(r −r1 ) ×(r2 −r1 ) = 0. |
144
Это уравнение легко преобразуется к виду |
|
r ×(r2 −r1 ) = r1 ×r2 . |
(3.4.15) |
И, наконец, это же уравнение в параметрической форме: |
|
r = r1 + t(r2 −r1 ). |
(3.4.16) |
L.5) Уравнение прямой на плоскости, проходящей через точку M0 (r0 ), перпендикулярно вектору n:
(r −r0 ) ·n = 0. |
(3.4.17) |
Это уравнение можно преобразовать к виду |
|
r ·n + λ = 0, |
(3.4.18) |
где λ некоторый скаляр.
P.1) Уравнение плоскости, проходящей через точку M0 (r0 ), перпендику-
лярно вектору n: |
|
(r −r0 ) ·n = 0, |
(3.4.19) |
или |
|
r ·n + λ = 0. |
(3.4.20) |
P.2) Уравнение плоскости, проходящей через точку M0 (r0 ), параллельно неколлинеарным векторам p и q:
(r −r0) ·p ·q = 0. |
(3.4.21) |
P.3) Уравнение плоскости, проходящей через точку M0 (r0 ), параллельно неколлинеарным векторам p и q:
r −r0 = t1 p + t2q. |
(3.4.22) |
P.4) Уравнение плоскости, проходящей через точки M1 (r1 ), M2 (r2 ) и
M3 (r3 ) :
(r −r1 ) ·(r2 −r1 ) ·(r3 −r1 ) = 0. |
(3.4.23) |
Рекомендуем читателю обратить особое внимание на уравнения (3.4.11), (3.4.17), (3.4.19), (3.4.21), (3.4.22) и вывести эти формулы.
§ 3.5. Кривые второго порядка
До сих пор мы рассматривались уравнения линейных объектов — прямых и плоскостей, и это были уравнения первой степени. Пусть на плоскости задана декартова прямоугольная система координат. Рассмотрим общее алгебраическое уравнение второго порядка
a11 x2 + 2a12 xy + a22 y2 + a1 x + a2 y + a0 = 0. |
(3.5.1) |
Возможны следующие случаи:
1) уравнению (3.5.1) не удовлетворяет ни одна точка плоскости. Например, если уравнение имеет вид x2 + y2 + 1 = 0;
145
2)этому уравнению удовлетворяет единственная точка. Например, x2 + y2 = 0;
3)уравнению удовлетворяют точки, лежащие на одной прямой. Например, уравнение x2 −2xy + y2 = 0 эквивалентно уравнению (x −y)2 = 0, т. е. x −y = 0 — а это прямая;
4)уравнению удовлетворяют точки, лежащие на двух прямых. Например, x2 −2xy + y2 −1 = 0 эквивалентно уравнению (x −y)2 = 1, или (x −y) =
±1, а это — две прямые;
5)уравнению (3.5.1) удовлетворяют точки, лежащие на некоторой кривой (в обыденном понимании этого термина); такую кривую называют кри-
вой второго порядка. |
|
|
|
|
|
|
Последний случай и будет нас интересовать в этом разделе. Оказывается, |
||||||
таких кривых может быть всего лишь три: эллипс, гипербола и парабола. |
||||||
Возьмем на плоскости вторую декар- |
y |
|
|
|
|
|
|
|
|
|
|
|
|
тову прямоугольную систему координат, |
|
|
|
|
|
|
определяемую началом O′ и базисными |
|
y ’ |
|
|
|
|
векторами i′ и j′ (рис. 3.14). |
|
|
|
|
|
|
В подробных курсах аналитической гео- |
|
|
|
|
|
x ’ |
метрии доказывается, что переход от од- |
j |
j ’ |
|
|
||
ной системы координат к другой сводится |
|
i ’ |
|
|||
|
|
|
||||
|
|
O’ |
|
|||
к параллельному переносу вдоль вектора |
O |
|
|
|
||
OO′ и последующему повороту осей на |
|
|
|
|
|
|
|
|
i |
|
|
x |
|
угол ϕ. |
|
|
|
|
||
|
|
|
|
|
||
|
|
Рис. 3.14 |
|
|||
|
|
|
|
|||
Правда, это будет в том случае, когда базисные векторы направлены |
||||||
так, что кратчайшие повороты от i к j и от i′ к j′ совершаются в одном |
||||||
направлении. |
y |
|
|
|
|
|
|
|
|
|
x ’ |
|
|
|
|
|
|
|
|
|
Если кратчайшие повороты от i к j и |
|
|
|
|
|
|
от i′ к j′ совершаются в противополож- |
|
|
i ’ |
|
|
|
ных направлениях (рис. 3.15), то нужно |
|
|
|
|
||
еще изменить направление оси ординат |
|
’ |
ϕ |
|
|
|
|
|
O |
|
|
|
|
на противоположное. Такое преобразова- |
j |
|
|
|
|
|
ние нельзя свести к параллельному пере- |
|
|
|
|
|
|
|
|
|
j ’ |
|
|
|
носу и повороту, не выводящему из плос- |
|
|
|
y ’ |
|
|
O |
|
|
|
|
||
кости Oxy. |
|
|
|
|
||
|
|
|
|
|
||
|
|
|
|
|
x |
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
Рис. 3.15 Можно доказать, что при преобразовании системы координат кривая
второго порядка останется кривой второго порядка, но уравнение этой кривой изменится.
146
|
y |
|
|
|
|
|
Рассмотрим, например, уравнение |
|
|
|
|
y ’ |
|
|
|
x2 + y2 −4x −4y + 7 = 0. Выделяя полные |
|
|
|
|
|
|
|
|
|
квадраты, запишем это уравнение в ви- |
|
y |
|
|
M |
|
|
де (x −2)2 + (y− −2)2 = 1. Это — окруж- |
|
|
O’ |
|
|
|
|
ность радиуса R = 1 с центром в точке |
||
2 |
|
|
|
|
|
|
O′(2, 2) (рис. 3.16). Если начало координат |
|
|
|
|
|
|
x ’ |
|||
|
|
|
|
|
|
перенести в точку O′, то уравнение при- |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
нимает более простой вид: x′2 + y′2 = 1. |
|
O |
|
|
|
|
|
При параллельном переносе системы ко- |
|
|
|
|
|
|
x |
|
x |
ординат формулы, связывающие коорди- |
|
|
|
2 |
|
|
наты точки M в той и другой системах |
||
|
|
|
|
|
|
|||
|
|
|
Рис. 3.16 |
|
|
координат, особенно просты. |
||
|
|
Пусть точка M в системе координат Oxy имеет координаты (x, y), а в |
||||||
системе координат O′x′y′ — (x′, y′). Тогда (рис. 3.16): OM = OO′ + O′M. Предположим, что точка O′ в системе координат Oxy имеет координаты (x0 , y0 ). Отсюда находим векторы OO′ = {x0 , y0 }, O′M = {x′, y′} и OM = {x, y}. Следовательно {x, y} = {x0 , y0 } + {x′, y′} и получаем формулы, связывающие
«старые» координаты (x, y) точки M с её «новыми» координатами (x′, y′)
x = x0 + x′,
y= y0 + y′.
Всвязи с этим возникают две задачи.
1.Как выбрать систему координат, чтобы уравнение кривой имело простейший, или, как говорят, канонический вид?
2.Если кривая второго порядка задана «сложным» уравнением (3.5.1), то как и к какой системе координат перейти, чтобы эта кривая имела каноническое уравнение?
Вторая задача рассматривается ниже в теории приведения квадратичных форм к каноническому виду. Мы же остановимся на первой задаче.
3.5.1. Эллипс
Определение 3.5.1. Эллипсом называется геометрическое место точек плоскости, для которых сумма расстояний до двух данных точек F1 и F2 этой плоскости, называемых фокусами, есть величина постоянная (и равная 2a).
Ясно, что должно выполняться неравенство 2a > F1 F2 .
147
Для вывода канонического уравнения эллипса проведем ось Ox через фокусы F1 и F2 , а ось Oy перпендикулярно оси Ox через середину отрезка F1 F2 (рис. 3.17). Если фокусы совпадают, то оси координат проводим через фокус произвольно.
y
M(x, y)
|
O |
|
F1 (−c, 0) |
F2 (c, 0) |
x |
|
Рис. 3.17
Пусть длина отрезка F1 F2 равна 2c. Тогда точки F1 и F2 имеют координаты (−c, 0) и (c, 0) соответственно.
Возьмем точку M(x, y) на плоскости. Она будет лежать на эллипсе тогда и только тогда, когда MF1 + MF2 = 2a. Используя формулу расстояния между
точками (2.3.10), получим |
|
q(x + c)2 + y2 + q(x −c)2 + y2 = 2a. |
(3.5.2) |
Это равенство является необходимым и достаточным условием принадлежности точки M(x, y) данному эллипсу.
Перенесем в последнем равенстве один из корней вправо и возведем обе
части в квадрат
q
(x + c)2 + y2 = 4a2 −4a (x −c)2 + y2 + (x −c)2 + y2 .
Упростив это равенство и оставив корень справа,получим q
cx −a2 = −a (x −c)2 + y2 .
Снова возводим обе части в квадрат
c2 x2 −2a2 cx + a4 = a2 (x2 −2cx + c2 + y2 )
или
(a2 −c2 )x2 + a2 y2 = (a2 −c2 )y2 .
В любом треугольнике сумма двух его сторон больше третьей стороны. Значит MF1 + MF2 > F1 F2 , т. е. 2a > 2c (рис. 3.17). Отсюда a2 −c2 > 0. Обозначая b2 = a2 −c2 , получаем
b2 x2 + a2 y2 = b2 a2 . |
|
|||||
Разделим обе части этого равенства на b2 a2 : |
|
|||||
|
x2 |
y2 |
(3.5.3) |
|||
|
|
+ |
|
|
= 1, |
|
2 |
b |
2 |
||||
|
a |
|
|
|
||
где |
|
|
|
|
||
b2 = a2 −c2 . |
(3.5.4) |
|||||
При возведении в квадрат равенства (3.5.2) могли появиться «лишние корни», то есть такие точки M(x, y), которые удовлетворяют уравнению (3.5.3), но не удовлетворяют уравнению (3.5.2). Пусть координаты точки
148
M(x, y) удовлетворяют уравнению (3.5.3). Из этого уравнения найдём y2 =
b2 |
1 − |
x2 |
и подставим в уравнение (3.5.2) |
|
|
|
|
|||||||||
a2 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s(x + c)2 + b2 − |
2 x2 |
+ s(x −c)2 + b2 − |
b2 x2 |
||||||||||
|
|
|
b |
|
= 2a. |
|||||||||||
|
|
|
a2 |
a2 |
||||||||||||
После несложных преобразований получим |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r(a + |
c |
+ r(a − |
c |
|
|
|
|
|||||
|
|
|
|
|
·x)2 |
|
|
·x)2 = 2a. |
|
|||||||
|
|
|
|
a |
a |
|
||||||||||
Из уравнения (3.5.3) очевидно, что |
x2 |
6 1, т. е. |x| 6 a, и так как c < a, то |
|||||||
a2 |
|||||||||
|
c |
|
c |
|
|
|
c |
||
|
|
< 1. Следовательно, a + |
|
x > 0 |
и a − |
|
x > 0. Поэтому равенство (3.5.2) |
||
a |
a |
a |
|||||||
представляет собой верное числовое равенство 2a = 2a, то есть точка M(x, y) с координатами, удовлетворяющими уравнению (3.5.3), лежит на эллипсе.
Уравнение (3.5.3) называется каноническим уравнением зллипса.
Числа a и b называются большой и малой полуосями эллипса (так как a2 = b2 + c2 , то a > b, отсюда и термины — большая и малая).
Отметим, что если полуоси равны a = b = R, то эллипс представляет собой окружность x2 + y2 = R2 с центром в начале координат.
3.5.2. Эллипс. Исследование формы
2 |
2 |
|
||
Из канонического уравнения эллипса |
x |
+ |
y |
= 1 получаем: |
2 |
2 |
|||
|
a |
|
b |
|
1) эллипс симметричен относительно осей координат и относительно
начала координат.
Действительно, в уравнение эллипса x и y входят в четных степенях, поэтому если точка M1 (x, y) лежит на эллипсе, то точки M2 (−x, y) M3 (−x, −y) и M4 (x, −y) также лежат на на нём. А эти точки обладают указанной сим-
метрией (рис. 3.18); |
|
|
|
|
|
|
||
|
y |
|
|
|
y |
|
|
|
M2 (−x, y) |
|
M1 (x, y) |
|
|
B(0, b) |
|||
|
O |
|
|
x |
C(−a, 0) |
|
A(a, 0) |
|
|
|
|
|
|
O |
|
x |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
M3 (−x, −y) |
|
M4 (x, −y) |
|
|
D(0, b) |
|||
|
|
|
|
|
|
|
− |
|
149

Рис. 3.18 |
Рис. 3.19 |
2)эллипс пересекается с осями координат в точках A(a, 0), B(0, b),
C(−a, 0) и D(0, −b).
Действительно, полагая в уравнении эллипса y = 0, получаем x2 = a2 , то есть x = ±a. Аналогично, при x = 0 имеем y = ±b (рис. 3.19). Точки A, B, C
иD называются вершинами эллипса. Отрезок CA = 2a называется большой осью эллипса, DB = 2b — малой осью;
3)эллипс содержится внутри прямоугольника −a 6 x 6 a, −b 6 y 6 b (рис. 3.19).
В самом деле, из канонического уравнения эллипса имеем: x2 6 1 и a2
y2 6 1. Отсюда x2 6 a2 и y2 6 b2 , что эквивалентно неравенствам −a 6 x 6 a, b2
−b 6 y 6 b;
4) в силу симметрии эллипса достаточно построить его график для пер-
вой четверти плоскости Oxy. В этой четверти x > 0 и y > 0. Из каноническо- r
го уравнения эллипса находим y = = b 1 − x2 . Используя производные, a2
можно показать, что при 0 < x < a первая производная y′ 6 0 и вторая про-
изводная y′′ 6 0. В дифференциальном исчислении будет доказано, что это r
означает монотонное убывание графика функции y = b 1 − x2 и что этот a2
график является выпуклой вверх кривой.
На основании свойств 1)–4) строим эллипс (рис. 3.20).
Заметим, что если в уравнении эллипса b > a, например, уравнение име-
ет вид x2 + y2 = 1, то это означает, что фокусы эллипса располагаются на
42 92
оси ординат и он «вытянут» вдоль этой оси (рис. 3.21). В самом деле, переобозначая оси координат x и y: x′ = y, y′ = −x, получим рассмотренный случай — эллипс с фокусами на оси Ox′.
150
