
- •ПРЕДИСЛОВИЕ
- •ВВЕДЕНИЕ
- •ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ИНЖЕНЕРНОЙ ГРАФИКИ
- •Элберт Хаббард
- •ПРИНЯТЫЕ ОБОЗНАЧЕНИЯ
- •ГЛАВА 1
- •ОСНОВНЫЕ ПОНЯТИЯ В ТЕОРИИ ИЗОБРАЖЕНИЯ ГЕОМЕТРИЧЕСКИХ ОБЪЕКТОВ
- •1. ЧТО ТАКОЕ НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ?
- •2. ГЕОМЕТРИЧЕСКОЕ МОДЕЛИРОВАНИЕ – ИНСТРУМЕНТ ПОЗНАНИЯ ДЕЙСТВИТЕЛЬНОСТИ
- •4. ПРОЕКЦИОННОЕ ОТОБРАЖЕНИЕ – АНАЛОГ ПОНЯТИЯ ФУНКЦИИ
- •Свойства центрального проецирования
- •Свойства параллельного проецирования
- •5. МЕТОД ДВУХ ИЗОБРАЖЕНИЙ
- •6. МОДЕЛЬ ТОЧКИ В ОРТОГОНАЛЬНЫХ ПРОЕКЦИЯХ
- •ВЫВОДЫ
- •ПРЯМАЯ ЛИНИЯ И ПЛОСКОСТЬ
- •1. ПОЛОЖЕНИЕ ПРЯМОЙ В ПРОСТРАНСТВЕ
- •3. ВЗАИМНОЕ ПОЛОЖЕНИЕ ДВУХ ПРЯМЫХ
- •4. ПОЛОЖЕНИЕ ПЛОСКОСТИ В ПРОСТРАНСТВЕ
- •5. РАСПОЛОЖЕНИЕ ПЛОСКОСТИ ОТНОСИТЕЛЬНО ОСНОВНЫХ ПЛОСКОСТЕЙ ПРОЕКЦИЙ
- •Проецирующая плоскость
- •Плоскость уровня
- •ВЫВОДЫ
- •УПРАЖНЕНИЕ
- •Задача № 1
- •Порядок выполнения
- •Задача № 2
- •Порядок выполнения
- •Задача № 3
- •Порядок выполнения
- •Задача № 4
- •Порядок выполнения
- •Задача № 5
- •Порядок выполнения
- •ГЛАВА 3
- •СПОСОБЫ ПРЕОБРАЗОВАНИЯ ПРОЕКЦИЙ
- •1. ПРИНАДЛЕЖНОСТЬ ПРЯМОЙ ЛИНИИ ПЛОСКОСТИ
- •1.1. ПРЯМАЯ ОБЩЕГО ПОЛОЖЕНИЯ В ПЛОСКОСТИ
- •1.2. ГЛАВНЫЕ ЛИНИИ ПЛОСКОСТИ
- •Линии уровня
- •Линии наибольшего наклона плоскости
- •2. СПОСОБЫ ПРЕОБРАЗОВАНИЯ ПРОЕКЦИЙ
- •2.1. ПЛОСКОПАРАЛЛЕЛЬНОЕ ПЕРЕМЕЩЕНИЕ
- •2.2. ВРАЩЕНИЕ ВОКРУГ ОСЕЙ, ПЕРПЕНДИКУЛЯРНЫХ ПЛОСКОСТЯМ ПРОЕКЦИЙ
- •2.3. ВРАЩЕНИЕ ВОКРУГ ОСЕЙ, ПАРАЛЛЕЛЬНЫХ ПЛОСКОСТЯМ ПРОЕКЦИЙ
- •2.4. ВРАЩЕНИЕ ВОКРУГ ОСЕЙ, ЛЕЖАЩИХ В ПЛОСКОСТЯХ ПРОЕКЦИЙ (СОВМЕЩЕНИЕ С ПЛОСКОСТЯМИ ПРОЕКЦИЙ)
- •2.5. ЗАМЕНА ПЛОСКОСТЕЙ ПРОЕКЦИЙ
- •ВЫВОДЫ
- •УПРАЖНЕНИЕ
- •ГЛАВА 4
- •ОБОБЩЕННЫЕ ПОЗИЦИОННЫЕ ЗАДАЧИ
- •1.1. ПРЯМАЯ ЛИНИЯ, ПАРАЛЛЕЛЬНАЯ ПЛОСКОСТИ
- •1.2. ПРЯМАЯ ЛИНИЯ, ПЕРЕСЕКАЮЩАЯ ПЛОСКОСТЬ (ОБЩИЙ СЛУЧАЙ)
- •1.3. ПРЯМАЯ ЛИНИЯ, ПЕРПЕНДИКУЛЯРНАЯ ПЛОСКОСТИ
- •2. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПЛОСКОСТЕЙ
- •2.1. ПЛОСКОСТИ ПАРАЛЛЕЛЬНЫЕ
- •2.2. ПЛОСКОСТИ ПЕРЕСЕКАЮЩИЕСЯ (ОБЩИЙ СЛУЧАЙ)
- •2.3. ПЛОСКОСТИ ВЗАИМНО ПЕРПЕНДИКУЛЯРНЫЕ
- •3. ВЗАИМНО ПЕРПЕНДИКУЛЯРНЫЕ ПРЯМЫЕ
- •4. ОБОБЩЕННЫЕ ПОЗИЦИОННЫЕ ЗАДАЧИ
- •4.1. ПЕРЕСЕЧЕНИЕ КРИВОЙ ЛИНИИ С ПОВЕРХНОСТЬЮ
- •4.2. ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ
- •4.3. ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА
- •ВЫВОДЫ
- •УПРАЖНЕНИЕ
- •Задача № 1
- •Порядок выполнения
- •Задача № 2
- •Порядок выполнения
- •Задача № 3
- •Порядок выполнения
- •Задача № 4
- •Порядок выполнения
- •Задача № 5
- •Порядок выполнения
- •ГЛАВА 5
- •1. ОБ АНАЛОГИИ МЕЖДУ ПОНЯТИЯМИ «ФУНКЦИЯ» И «ОТОБРАЖЕНИЕ»
- •2. ПЕРСПЕКТИВНАЯ КОЛЛИНЕАЦИЯ
- •Теорема Дезарга
- •Гомология
- •3. ПЕРСПЕКТИВНО-АФФИННОЕ (РОДСТВЕННОЕ) СООТВЕТСТВИЕ
- •4. СРАВНЕНИЕ ДВУХ ГОМОЛОГИЙ
- •ВЫВОДЫ
- •УПРАЖНЕНИЕ
- •Порядок выполнения
- •ГЛАВА 6
- •ПРОЕКЦИОННЫЕ МОДЕЛИ ТРЕХМЕРНЫХ ОБЪЕКТОВ
- •1. ВНЕШНЯЯ ФОРМА ПРЕДМЕТОВ И НЕОБХОДИМОСТЬ ВЫЯВЛЕНИЯ ИХ ВНУТРЕННИХ КОНТУРОВ
- •2. СИСТЕМЫ РАСПОЛОЖЕНИЯ ИЗОБРАЖЕНИЙ
- •3. ВИДЫ
- •3.1. ОСНОВНЫЕ ВИДЫ
- •3.2. ДОПОЛНИТЕЛЬНЫЕ ВИДЫ
- •3.3. МЕСТНЫЕ ВИДЫ
- •4. РАЗРЕЗЫ
- •4.1. ВИДЫ РАЗРЕЗОВ
- •4.2. ОБОЗНАЧЕНИЕ РАЗРЕЗОВ
- •5. СЕЧЕНИЯ
- •ВЫВОДЫ
- •УПРАЖНЕНИЕ
- •Задача № 1
- •Порядок выполнения
- •Задача № 2
- •Порядок выполнения
- •КРИВЫЕ ЛИНИИ
- •1. СПОСОБЫ ОБРАЗОВАНИЯ КРИВЫХ ЛИНИЙ
- •2. КЛАССИФИКАЦИЯ КРИВЫХ ЛИНИЙ
- •3. СПОСОБЫ ЗАДАНИЯ КРИВЫХ ЛИНИЙ
- •4. КАСАТЕЛЬНАЯ И НОРМАЛЬ К КРИВОЙ ЛИНИИ
- •5. УРАВНЕНИЯ КАСАТЕЛЬНОЙ И НОРМАЛИ
- •6. ВЕКТОР-ФУНКЦИЯ
- •7. КРИВИЗНА КРИВОЙ
- •8. КРУГ КРИВИЗНЫ
- •9. ЭВОЛЮТА И ЭВОЛЬВЕНТА
- •10. КРИВИЗНА ОКРУЖНОСТИ
- •11. КРИВЫЕ ЛИНИИ ВТОРОГО ПОРЯДКА
- •11.1. ЭЛЛИПС
- •11.2. ПАРАБОЛА
- •11.3. ГИПЕРБОЛА
- •12. КОНИЧЕСКИЕ СЕЧЕНИЯ
- •13. ПРОЕКЦИИ КРИВЫХ ЛИНИЙ
- •14. ЭЛЛИПС – ФИГУРА, РОДСТВЕННАЯ ОКРУЖНОСТИ
- •15. ОКРУЖНОСТЬ В ПЛОСКОСТИ ОБЩЕГО ПОЛОЖЕНИЯ
- •15.2. ОПРЕДЕЛЕНИЕ ВЕЛИЧИНЫ МАЛОЙ ОСИ ЭЛЛИПСА МЕТОДОМ ЗАМЕНЫ ПЛОСКОСТЕЙ ПРОЕКЦИЙ
- •15.3. ОПРЕДЕЛЕНИЕ ВЕЛИЧИНЫ МАЛОЙ ОСИ ЭЛЛИПСА С ПРИМЕНЕНИЕМ ЛИНИИ НАИБОЛЬШЕГО НАКЛОНА ПЛОСКОСТИ
- •ВЫВОДЫ
- •УПРАЖНЕНИЕ
- •Порядок выполнения
- •ГЛАВА 8
- •КРИВЫЕ ЛИНИИ, ИМЕЮЩИЕ ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ.
- •ОБВОДЫ ПРИ ПРОЕКТИРОВАНИИ ПОВЕРХНОСТЕЙ
- •1. НЕКОТОРЫЕ ПЛОСКИЕ КРИВЫЕ, ИМЕЮЩИЕ ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ
- •1.1. ЦИКЛИЧЕСКИЕ КРИВЫЕ
- •Циклоида
- •Эпициклоиды
- •Гипоциклоиды
- •1.2. СПИРАЛИ
- •1.3. ПОДЕРЫ
- •2.ПЛОСКИЕ СОСТАВНЫЕ КРИВЫЕ ЛИНИИ (ОБВОДЫ) ПРИ ПРОЕКТИРОВАНИИ ПОВЕРХНОСТЕЙ
- •2.1. АППРОКСИМАЦИЯ ТОЧЕЧНЫХ МАССИВОВ
- •2.3. ХАРАКТЕРНЫЕ ТОЧКИ КРИВЫХ
- •2.4. ПОРЯДОК ГЛАДКОСТИ ОБВОДОВ
- •2.5. ОСНОВНЫЕ СПОСОБЫ ПОСТРОЕНИЯ ОБВОДОВ
- •2.5.1. ИНТЕРПОЛЯЦИЯ ДУГАМИ ОКРУЖНОСТЕЙ
- •2.5.2. ИНТЕРПОЛЯЦИЯ КРИВЫМИ ВТОРОГО ПОРЯДКА
- •2.5.3. ИНТЕРПОЛЯЦИЯ ОБВОДОВ СПЛАЙН-ФУНКЦИЯМИ
- •ВЫВОДЫ
- •ГЛАВА 9
- •МНОГОГРАННЫЕ ПОВЕРХНОСТИ И МНОГОГРАННИКИ.
- •СИСТЕМАТИЗАЦИЯ ПОВЕРХНОСТЕЙ
- •1. МНОГОГРАННЫЕ ПОВЕРХНОСТИ
- •2. НЕКОТОРЫЕ ВИДЫ МНОГОГРАННИКОВ
- •3. ПЕРЕСЕЧЕНИЕ МНОГОГРАННИКА ПЛОСКОСТЬЮ
- •5. ВЗАИМНОЕ ПЕРЕСЕЧЕНИЕ МНОГОГРАННИКОВ
- •6. РАЗВЕРТКИ МНОГОГРАННИКОВ
- •6.1. СПОСОБ НОРМАЛЬНОГО СЕЧЕНИЯ
- •6.2. СПОСОБ РАСКАТКИ
- •6.3. СПОСОБ ТРЕУГОЛЬНИКОВ (ТРИАНГУЛЯЦИИ)
- •7. СИСТЕМАТИЗАЦИЯ ПОВЕРХНОСТЕЙ
- •ВЫВОДЫ
- •УПРАЖНЕНИЕ
- •Порядок выполнения
- •СЛОЖНЫЕ ПОВЕРХНОСТИ
- •1. ОПРЕДЕЛЕНИЕ ПОВЕРХНОСТИ
- •2. СПОСОБЫ ОБРАЗОВАНИЯ ПОВЕРХНОСТЕЙ
- •2.1. ОБРАЗОВАНИЕ ПОВЕРХНОСТЕЙ ПРИ ПОМОЩИ ДВИЖУЩЕЙСЯ ЛИНИИ
- •2.2. ОБРАЗОВАНИЕ ПОВЕРХНОСТЕЙ ПРИ ПОМОЩИ ДВИЖУЩЕЙСЯ ПОВЕРХНОСТИ
- •3. СПОСОБЫ ЗАДАНИЯ ПОВЕРХНОСТЕЙ
- •3.1. ГРАФИЧЕСКИЙ СПОСОБ ЗАДАНИЯ КИНЕМАТИЧЕСКИХ ПОВЕРХНОСТЕЙ
- •3.2. АНАЛИТИЧЕСКИЙ СПОСОБ ЗАДАНИЯ ПОВЕРХНОСТЕЙ
- •3.3. ПРИМЕР АНАЛИТИЧЕСКОГО СПОСОБА ЗАДАНИЯ ПОВЕРХНОСТИ
- •4. ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ ПОВЕРХНОСТЕЙ
- •4.1. ТРЕХГРАННИК ФРЕНЕ
- •4.2. ЕСТЕСТВЕННЫЕ КООРДИНАТЫ ПРОСТРАНСТВЕННОЙ КРИВОЙ
- •5. КРИВЫЕ ЛИНИИ НА СФЕРЕ
- •6. КАСАТЕЛЬНЫЕ И НОРМАЛИ К ПОВЕРХНОСТИ ПРИ ОБРАБОТКЕ ЕЕ НА СТАНКАХ С ЧПУ
- •7.2. КАРКАСНО-КИНЕМАТИЧЕСКИЙ МЕТОД ПРОЕКТИРОВАНИЯ
- •ВЫВОДЫ
- •УПРАЖНЕНИЕ
- •Порядок выполнения
- •ПОВЕРХНОСТИ ВРАЩЕНИЯ И ВИНТОВЫЕ
- •1. ПОВЕРХНОСТИ ВРАЩЕНИЯ
- •3. ПРИМЕРЫ ПОВЕРХНОСТЕЙ ВРАЩЕНИЯ
- •3.1. СФЕРА
- •3.2. ЦИЛИНДР ВРАЩЕНИЯ
- •3.3. КОНУС ВРАЩЕНИЯ
- •3.4. ГИПЕРБОЛОИД ВРАЩЕНИЯ
- •4. ВИНТОВЫЕ ПОВЕРХНОСТИ
- •4.1. ПРЯМОЙ ГЕЛИКОИД
- •4.2. ДРУГИЕ ВИДЫ ВИНТОВЫХ ПОВЕРХНОСТЕЙ
- •ВЫВОДЫ
- •УПРАЖНЕНИЕ
- •Порядок выполнения
- •ЛИНЕЙЧАТЫЕ ПОВЕРХНОСТИ
- •1. СПОСОБ ОБРАЗОВАНИЯ ПОВЕРХНОСТЕЙ ДВИЖЕНИЕМ ПРЯМОЙ ЛИНИИ
- •2.1. КОНИЧЕСКИЕ ПОВЕРХНОСТИ
- •2.2. ЦИЛИНДРИЧЕСКИЕ ПОВЕРХНОСТИ
- •3. ЛИНЕЙЧАТЫЕ ПОВЕРХНОСТИ
- •3.1. ЦИЛИНДРОИД
- •3.2. КОНОИД
- •3.3. ГИПЕРБОЛИЧЕСКИЙ ПАРАБОЛОИД (КОСАЯ ПЛОСКОСТЬ)
- •ВЫВОДЫ
- •УПРАЖНЕНИЕ
- •Порядок выполнения
- •ГЛАВА 13
- •РАЗВЕРТКИ ПОВЕРХНОСТЕЙ
- •1. ПЛОСКОСТЬ, КАСАТЕЛЬНАЯ К ПОВЕРХНОСТИ
- •1.1. ОСНОВНЫЕ ПОНЯТИЯ
- •1.2. ПОСТРОЕНИЕ КАСАТЕЛЬНОЙ ПЛОСКОСТИ
- •2. РАЗВЕРТКИ ПОВЕРХНОСТЕЙ
- •2.1. ПОРЯДОК ПОСТРОЕНИЯ РАЗВЕРТОК В ОБЩЕМ СЛУЧАЕ
- •2.2. ОСНОВНЫЕ СВОЙСТВА РАЗВЕРТЫВАЮЩИХСЯ ПОВЕРХНОСТЕЙ
- •2.3. ПРИМЕРЫ РАЗВЕРТЫВАНИЯ КРИВЫХ ПОВЕРХНОСТЕЙ
- •Прямой круговой цилиндр
- •Наклонный цилиндр
- •Конус
- •2.4. РАЗВЕРТКИ НЕРАЗВЕРТЫВАЮЩИХСЯ ПОВЕРХНОСТЕЙ
- •ВЫВОДЫ
- •УПРАЖНЕНИЕ
- •Задача № 1
- •Порядок выполнения
- •Задача № 2
- •Порядок выполнения
- •Задача № 3
- •Порядок выполнения
- •Создание конуса с вырезом
- •Создание развертки
- •Задача № 4
- •Порядок выполнения
- •АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ
- •1. ОСНОВНЫЕ ПОНЯТИЯ
- •2. СУТЬ СПОСОБА ПОЛУЧЕНИЯ АКСОНОМЕТРИЧЕСКИХ ПРОЕКЦИЙ
- •5. СТАНДАРТНЫЕ ВИДЫ АКСОНОМЕТРИЧЕСКИХ ПРОЕКЦИЙ
- •5.1. ПРЯМОУГОЛЬНАЯ ИЗОМЕТРИЯ
- •5.1.1. ОКРУЖНОСТЬ В ПРЯМОУГОЛЬНОЙ ИЗОМЕТРИИ
- •5.2. ПРЯМОУГОЛЬНАЯ ДИМЕТРИЯ
- •6. КОСОУГОЛЬНЫЕ АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ
- •6.1. ФРОНТАЛЬНАЯ ИЗОМЕТРИЧЕСКАЯ ПРОЕКЦИЯ
- •6.2. ГОРИЗОНТАЛЬНАЯ ИЗОМЕТРИЧЕСКАЯ ПРОЕКЦИЯ
- •6.3. ФРОНТАЛЬНАЯ ДИМЕТРИЧЕСКАЯ ПРОЕКЦИЯ
- •ВЫВОДЫ
- •ГЛАВА 15
- •1. ПАРАМЕТРИЗАЦИЯ МАКРОГЕОМЕТРИИ ПОВЕРХНОСТЕЙ ТЕХНИЧЕСКИХ ИЗДЕЛИЙ
- •1.3. ЗАДАНИЕ РАЗМЕРОВ
- •1.3.1. БАЗИРОВАНИЕ И БАЗЫ
- •1.3.2. КОЛИЧЕСТВО РАЗМЕРОВ ДЛЯ ПОЛНОГО ОПРЕДЕЛЕНИЯ ФОРМЫ ДЕТАЛЕЙ
- •1.3.3. РАЗМЕРЫ ФОРМЫ И РАЗМЕРЫ ПОЛОЖЕНИЯ ПОВЕРХНОСТЕЙ
- •1.3.4. КОНСТРУКТИВНАЯ НЕОПРЕДЕЛЕННОСТЬ БАЗ
- •1.4. НАНЕСЕНИЕ РАЗМЕРОВ
- •1.5. ОСЕВЫЕ И ЦЕНТРОВЫЕ ЛИНИИ
- •2. ПАРАМЕТРИЗАЦИЯ МИКРОГЕОМЕТРИИ ПОВЕРХНОСТЕЙ ТЕХНИЧЕСКИХ ИЗДЕЛИЙ
- •ВЫВОДЫ
- •УПРАЖНЕНИЕ
- •Задача № 1
- •Задача № 2
- •Порядок выполнения
- •ЗАКЛЮЧЕНИЕ
- •БИБЛИОГРАФИЧЕСКИЙ СПИСОК
- •ОГЛАВЛЕНИЕ
Г л а в а 15. Параметризация макро- и микрогеометрии поверхностей технических изделий |
355 |
1.3.3. РАЗМЕРЫ ФОРМЫ И РАЗМЕРЫ ПОЛОЖЕНИЯ ПОВЕРХНОСТЕЙ
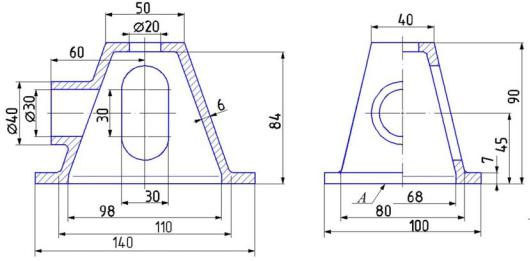
К размерам формы поверхностей относятся размеры определенных геометрических элементов. У детали, показанной на рис. 18, к таким размерам относятся:
•размеры 90; 100; 140; 40; 50;
•размеры 30 и 30 (фасонного выреза в наклонных стенках детали);
•размер 40 диаметра прилива;
•размер 30 диаметра отверстия в приливе;
•размер 20 диаметра отверстия на верхнем основании;
•размер 7 (толщины основания детали);
•размеры 98; 68; 84 внутреннего контура.
Рис. 18
К другой группе размеров относятся размеры, определяющие положение отмеченных геометрических элементов относительно поверхностей исходной внешней формы и других элементов:
•размер 45 указывает расстояние от привалочной плоскости А до оси отверстия в приливе и совпавшей с ней оси симметрии фасонного выреза;
•размер 60 задает расстояние от вертикальной оси до торца прилива;
•размер 6 (толщина стенок) определяет положение внутреннего контура относительно внешнего.
Различают размеры рабочие (исполнительные), каждый из которых используют при изготовлении изделия и его приемке (контроле), и справочные, ука-
356 |
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ИНЖЕНЕРНОЙ ГРАФИКИ |
зываемые только для большего удобства пользования чертежом. Измерение этих размеров при изготовлении изделия не допускается. Справочные размеры отмечают знаком «*», а в технических требованиях, расположенных над основной надписью, записывают: «* Размер (ы) для справки (вок)».
1.3.4. КОНСТРУКТИВНАЯ НЕОПРЕДЕЛЕННОСТЬ БАЗ
Конструктивная неопределенность баз – это неотличимость элементов детали, которые могут быть использованы в качестве технологических и измерительных баз, или наличие одной или нескольких пар симметрично расположенных и равных по величине размеров.
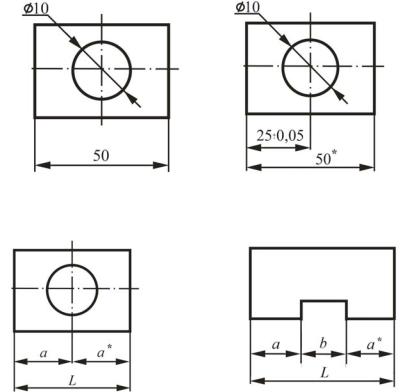
Задание размеров для таких деталей согласно ГОСТ 2.307–68 показано в двух вариантах на рис. 19, а, б.
Несимметричность отв. 10 |
* Размер для справок |
относительно контура не более… |
|
а |
б |
* Размер для справок |
* Размер для справок |
в |
г |
|
Рис. 19 |
Г л а в а 15. Параметризация макро- и микрогеометрии поверхностей технических изделий |
357 |
Оба варианта предусматривают определенную последовательность выполнения технологических операций: сначала выполнить отверстие, а затем обработать контур. Указание справочного размера на рис. 19, б теряет смысл, так как он выполняется всегда точнее, чем если бы был свободным. Поэтому в разных отраслях промышленности, например в отраслевом стандарте ОСТ НТО 010. 031 радиоэлектронной промышленности, предлагаются другие варианты назначения размеров. Они показаны на рис. 19, в, г и рекомендуются как предпочтительные.
1.4. НАНЕСЕНИЕ РАЗМЕРОВ
Правила нанесения размеров на чертежах установлены в ГОСТ 2.307–68, а также частично в ГОСТ 2.109–68.
Как уже было сказано выше, задать размеры – это значит определить, какие размеры нужны. Это первостепенная и важная задача конструктора, требующая для своего решения большого опыта и знаний. Нанесение же размеров требует только знания определенных правил, изложенных в указанных выше стандартах. Поэтому, грамотно определив, какие именно размеры нужны для конкретной детали, следует нанести их на чертеже по этим правилам.
1.5.ОСЕВЫЕ И ЦЕНТРОВЫЕ ЛИНИИ
Снанесением размеров связан вопрос о проведении на чертежах осевых и центровых линий, которые необходимы при изготовлении деталей. Они позволяют правильно задать места обработки – сверления отверстий, фрезерования пазов и т. п. Эти линии проводят на чертеже для выявления геометрических осей и центров и проекций плоскостей симметрии.
На рис. 20 показана деталь с цилиндрическим отверстием. Линия а1 на виде сверху выявляет ось отверстия. Центровые линии b позволяют координировать центр двумя размерами: 20 и 30.
Иногда смешивают два вида симметрии: симметрию детали в натуре и симметрию того или иного вида. Об этом подробно сказано в работе С.В. Розова [24], в которой приведены соответствующие иллюстрации. Так, на чертеже детали (рис. 21) проведены линии симметрии детали – проекции плоскостей симметрии α и β.
Кроме этих осей проведена горизонтальная ось симметрии профильного вида детали, что является ошибочным. На чертеже принято проводить оси симметрии детали, а не ее видов. Симметричная деталь всегда имеет симмет-
358 |
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ИНЖЕНЕРНОЙ ГРАФИКИ |
Рис. 20
Рис. 21
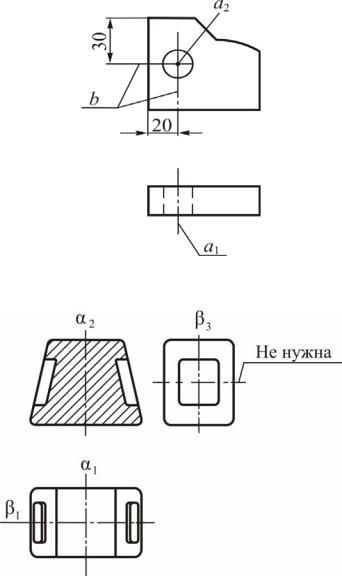
ричный вид на соответствующей плоскости проекций, а симметричный вид не всегда говорит о том, что деталь симметрична. Деталь (рис. 22) имеет одну плоскость симметрии α. Проекции плоскости симметрии α2 и α1 проводят на
чертеже штрихпунктирными линиями; буквенные обозначения не ставят.

Г л а в а 15. Параметризация макро- и микрогеометрии поверхностей технических изделий |
359 |
а б Рис. 22
Линия а3 является осевой линией цилиндрической части детали. Линия b2 есть центровая линия окружности, в виде которой изобразилась цилиндрическая часть детали на плоскости П2; вторая центровая линия с2 совпала с осью симметрии детали. Все поверхности вращения должны иметь на чертеже геометрическую ось (вращения) и соответствующие центровые линии. Геометрическую ось поверхности вращения и центровые линии проводят и в том случае, когда симметрия детали нарушена сечением или вырезом (рис. 23, а, б).
а
б
в
Рис. 23
360 |
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ИНЖЕНЕРНОЙ ГРАФИКИ |
Цилиндрическая деталь – |
штифт, имеет три плоскости симметрии |
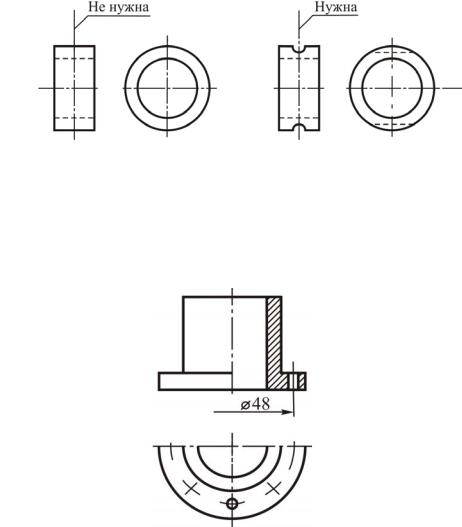
(рис. 23, в), однако проекцию плоскости симметрии, перпендикулярную к оси цилиндра, не следует изображать в виде осевой линии. То же подтверждается чертежом кольца (рис. 24, а): вторая осевая линия на главном виде не проводится. Если же кольцо имеет в середине выточку или отверстие, вторую осевую линию проводят (рис. 24, б).
а |
б |
Рис. 24
На чертежах деталей, имеющих ряд цилиндрических отверстий, расположенных на одной центровой окружности, не следует наносить горизонтальные и вертикальные центровые линии. В качестве одной центровой должна быть принята общая центровая окружность, в качестве второй – радиальная центровая, т. е. центровая, идущая в общий центр, по радиусу (рис. 25).
Рис. 25
При соединении вида с разрезом допускается не проводить осевых линий отверстий на виде; размерную линию в этом случае обрывают.
Г л а в а 15. Параметризация макро- и микрогеометрии поверхностей технических изделий |
361 |
1.6.ПРЕДЕЛЬНЫЕ ОТКЛОНЕНИЯ РАЗМЕРОВ
ИУКАЗАНИЕ ИХ НА ЧЕРТЕЖАХ
Размеры, указанные на чертеже, являются либо расчетными, либо назначенными из конструктивных или технологических соображений. Такие размеры называются номинальными.
Существует много причин, не позволяющих изготовить деталь с абсолютно точными размерами, поэтому конструктор указывает предельные отклонения их от номинальных, которые допустимы для обеспечения годности детали (изделия). В связи с этим различают наибольший предельный размер и наименьший. Предельные отклонения от номинального размера проставляются на чертеже рядом с этим размером со знаками плюс (+) и минус (–).
Предельные отклонения от номинальных размеров для многих видов соединений стандартизованы и даются в виде таблиц. В таблицах предельные отклонения указывают в микрометрах, а на чертежах – в миллиметрах более мелким шрифтом, например:
40+−0,030,013 ; 40−−0,0130,024 ; 40+0,011 .
При равенстве абсолютных величин отклонений их величину указывают один раз со знаком ± , например:
70 ± 0,2; 110° ± 20′.
Разность между наибольшим и наименьшим предельными значениями того или иного параметра называется допуском. Допуск определяет величину допустимого рассеяния действительных размеров годных деталей в партии, т. е. заданную точность изготовления.
Поле допуска – поле, ограниченное верхним и нижним отклонениями; задается его положением относительно номинального размера.
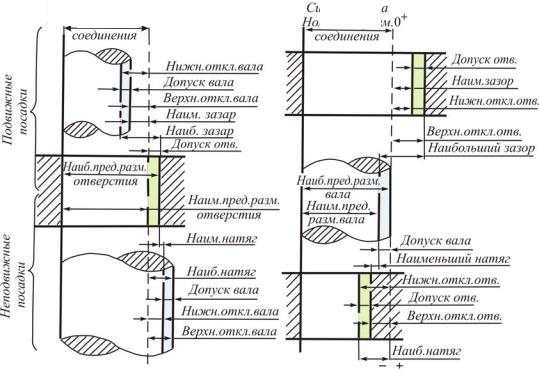
При соединении двух деталей образуется посадка. Посадкой называется характер соединения двух деталей, определяемый величиной получающихся зазоров или натягов. Она обеспечивает свободу относительного перемещения соединяемых деталей или степень сопротивления их взаимному смещению. В зависимости от взаимного расположения предельных отклонений отверстия и вала посадка может быть с зазором, с натягом или переходной, при которой возможно получение как зазора, так и натяга (рис. 26).
Внастоящее время большинство стран мира применяют системы допусков
ипосадок ISO. Стандартные посадки обозначаются буквой (буквами) латинского алфавита и цифрой. При этом заглавными буквами обозначают посадки отверстия, строчными – вала. Цифра в обозначении посадки соответствует номеру квалитета (степени точности).
362 |
|
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ИНЖЕНЕРНОЙ ГРАФИКИ |
||
|
Системаотверстия |
|
|
|
|
Системавала |
|||
|
Номинальн. разм. 0+ |
|
Номинальн. разм. 0+ |
|
|
|
|
|
|
а |
б |
Рис. 26
В каждом изделии детали разного назначения изготавливают с различной точностью. Для нормирования требуемых уровней точности установлены квалитеты изготовления деталей и изделий.
Под квалитетом понимают совокупность допусков, характеризуемых постоянной относительной точностью для всех размеров данного диапазона (например, от 1 до 500 мм). Точность в пределах одного квалитета изменяется только в зависимости от номинального размера. Квалитет определяет величину допуска на изготовление, а следовательно, и соответствующие методы и средства обработки деталей машин.
Разные виды посадок для данного квалитета и интервала номинальных размеров образуются либо за счет изменения размеров вала при неизменном основном отверстии (система отверстия), либо за счет изменения размеров отверстия при неизменном размере основного вала (система вала).
Система отверстия характеризуется тем, что в ней для всех посадок одной и той же степени точности (одного квалитета), отнесенных к одному и тому же
Г л а в а 15. Параметризация макро- и микрогеометрии поверхностей технических изделий |
363 |
номинальному диаметру, предельные размеры отверстия остаются постоянными. Различные посадки в системе отверстия достигаются соответствующим изменением предельных размеров вала. В системе отверстия наименьшим предельным размером отверстия является его номинальный размер.
Система вала характеризуется тем, что в ней для всех посадок одной и той же степени точности (одного квалитета), отнесенных к одному и тому же номинальному диаметру, предельные размеры вала остаются постоянными.
Различные посадки в системе вала достигаются за счет соответствующего изменения предельных размеров отверстия. В системе вала наибольшим предельным размером вала является его номинальный размер.
Допуск отверстия в системе отверстия всегда направлен в сторону увеличения диаметра отверстия (в тело), а допуск вала в системе вала – в сторону уменьшения диаметра вала (в тело).
Вмашиностроении принята преимущественно система отверстия, так как обработка вала проще, чем обработка отверстия.
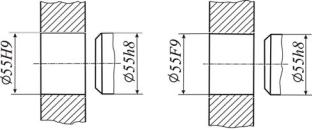
Всистеме отверстия (рис. 27, а) нижнее предельное отклонение размера основного отверстия равно нулю и условно обозначается буквой H. Посадки образуются за счет изменения размера вала при неизменном размере основного отверстия.
а б Рис. 27
В системе вала (рис. 27, б) верхнее отклонение размера основного вала равно нулю и условно обозначается буквой h. Посадки образуются за счет изменения предельных размеров отверстия. Система вала применяется в особых случаях, например при расположении на длинном валу нескольких деталей, имеющих различные посадки.
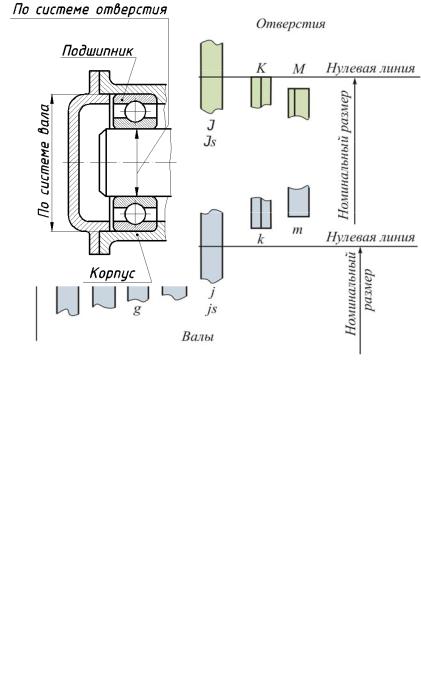
На рис. 28 показан фрагмент схемы расположения полей допусков для нескольких квалитетов отверстий и валов. Иногда размеры одного изделия выполняют в разных системах, например, наружный и внутренний диаметры подшипника (рис. 29).
364 |
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ИНЖЕНЕРНОЙ ГРАФИКИ |
Рис. 28
Рис. 29
Г л а в а 15. Параметризация макро- и микрогеометрии поверхностей технических изделий |
365 |
При разработке рабочих чертежей деталей конструктор назначает характер сопряжения их в сборочной единице и находит соответствующие квалитеты для размеров по таблицам.
1.7.ОТКЛОНЕНИЯ ФОРМЫ И РАСПОЛОЖЕНИЯ ПОВЕРХНОСТЕЙ
ИУКАЗАНИЕ ИХ НА ЧЕРТЕЖЕ
Под отклонением формы поверхности (или профиля) понимают отклонение формы реальной поверхности (реального профиля) от формы номинальной поверхности (номинального профиля). В основу нормирования и количественной оценки отклонения формы и расположения поверхностей положен принцип прилегающих прямых, поверхностей и профиля [22].
Прилегающие поверхности и профили соответствуют условиям сопряжения деталей при посадках с нулевым зазором. При измерении прилегающими поверхностями служат рабочие поверхности контрольных плит, интерференционных стекол, лекальных и поверочных линеек, калибров, контрольных оправок и т. п.
Количественно отклонение формы оценивается наибольшим расстоянием от точек реальной поверхности (профиля) до прилегающей поверхности (профиля) по нормали к последней.
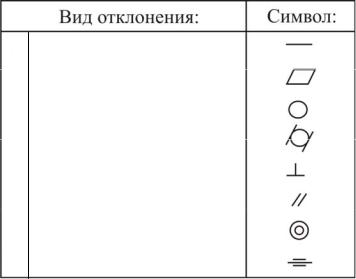
Приведем несколько знаков, установленных ГОСТ 2.308–79, определяющих вид отклонения (допуска) формы поверхностей.
Допуск
Вид допуска |
|
Знак |
прямолинейности
плоскостности
круглости
цилиндричности
перпендикулярности
параллельности
соосности
симметричности
366 |
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ИНЖЕНЕРНОЙ ГРАФИКИ |
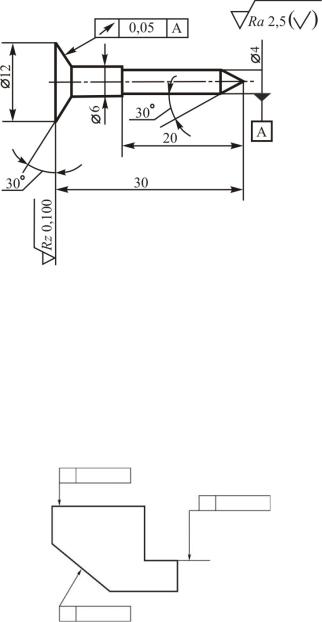
Пределы торцового или радиального биения (суммарный допуск формы и расположения) обозначают стрелкой. На рис. 30, приведенном в работе [23], изображена деталь с обозначением такого биения.
Рис. 30
Соответствующие данные о допуске указывают в прямоугольной рамке, выполняемой тонкими линиями, разделенной на две и более части, в которых помещают: в первой части – знак допуска по таблице, во второй – числовое значение допуска в миллиметрах, выбираемое из ГОСТ 24643–81, в третьей (и последующих) – буквенное обозначение базы (баз) или поверхности, с которой связан допуск расположения. Высота цифр, букв и знаков должна быть равна размеру шрифта размерных чисел. Рамку соединяют с элементом, к которому относится допуск, тонкой линией, заканчивающейся стрелкой. Соединительная линия может быть прямой или ломаной (рис. 31).
Рис. 31
Г л а в а 15. Параметризация макро- и микрогеометрии поверхностей технических изделий |
367 |
При этом если допуск относится к поверхности, то соединительная линия не должна быть продолжением размерной линии (рис. 32, а), если допуск относится к оси или плоскости симметрии, то соединительная линия должна быть продолжением размерной (рис. 32, б, в).
а |
б |
в |
Рис. 32
Базы обозначают зачерненным равносторонним треугольником, основание которого располагают на контурной линии поверхности (или ее продолжении), являющейся базовой. Высота треугольника должна быть равна размеру шрифта размерных чисел.
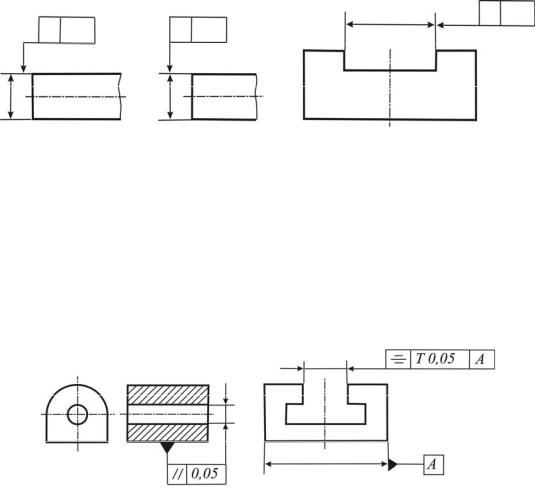
На рис. 33 приведены примеры обозначения допусков отклонений от расположения поверхностей:
а – допуск параллельности оси отверстия относительно основания 0,05 мм; б – допуск симметричности паза Т 0,05 мм.
а |
б |
Рис. 33
База – плоскость симметрии поверхностей А (сопоставьте с рис. 32, в). Пример применения знака отклонения от соосности (допуск соосности) дан
на рис. 34.
