Задача № 4

Построить точку пересечения прямой, заданной отрезком АВ: А (120, 15, 90), В (80, 85, 65), с плоскостью, заданной треугольником CDE: С (110, 25, 110),

D (230, 85, 80), E (60, 40, 60).

Порядок выполнения

Установить ПСК в заданную плоскость.

1.Построить проекцию отрезка АВ на эту плоскость.

2.Отметить точку пересечения отрезка АВ с его проекцией. На рис. 31 показан пример выполненной задачи № 4.

Рис. 31

Задача № 5

Построить линию пересечения двух плоскостей, заданных треугольниками ABC и DEF. Координаты вершин треугольников: А (175, 75, 45), В (85, 25, 95),

С (35, 85, 15), D (150, 30, 10), E (100, 120, 80), F (10, 20, 40).

Порядок выполнения

Искомая линия может быть найдена по двум точкам пересечения прямых одной плоскости с другой плоскостью.

Для этого нужно дважды решить задачу № 4 о пересечении прямой линии с плоскостью.

На рис. 32 показан пример выполненной задачи № 5.

Рис. 32

Решение приведенных задач методами виртуального моделирования полезно для лучшего усвоения изучаемого материала.

ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ

ИСАМОПОДГОТОВКИ

1.Какое взаимное положение могут занимать две плоскости?

2.Каков признак параллельности двух плоскостей?

3.Как взаимно располагаются фронтальные следы двух параллельных между собой фронтально проецирующих плоскостей?

4.В чем заключается в общем случае способ построения точки пересечения прямой с плоскостью?

5.Как определить видимость при пересечении прямой с плоскостью?

6.Чем определяется взаимная параллельность двух плоскостей?

7.Как проверить на чертеже, параллельны ли одна другой заданные плоскости?

8.Как располагаются проекции перпендикуляра к плоскости?

9.Как построить взаимно перпендикулярные плоскости?

ГЛАВА 5

СООТВЕТСТВИЕ ПЛОСКИХ ПОЛЕЙ* ПРИ ЦЕНТРАЛЬНОМ

И ПАРАЛЛЕЛЬНОМ ПРОЕЦИРОВАНИИ

Об аналогии между понятиями «функция» и «отображение» ≈ Перспективная коллинеация ≈ Перспективно-аффинное (родственное)

соответствие ≈ Сравнение двух гомологий

Мы уже отмечали тот факт, что прямоугольное параллельное проецирование является основным методом получения изображений в инженерной графике как частный случай параллельного, а параллельное, в свою очередь, является частным случаем центрального.

Посмотрим, как эти частные случаи связаны с общей теорией получения проекций геометрических образов. Но сначала об аналогии между понятиями «функция» и «отображение».

1.ОБ АНАЛОГИИ МЕЖДУ ПОНЯТИЯМИ «ФУНКЦИЯ»

И«ОТОБРАЖЕНИЕ»

Известно, что одним из фундаментальных понятий современной математики является понятие функции: y = f(x). У однозначных функций каждому значению x соответствует единственное значение y.

Геометрическим аналогом однозначной функции является ОТОБРАЖЕНИЕ.

Отображением одной геометрической фигуры на другую называют такое соответствие между ними, когда каждой точке первой фигуры отвечает един-

* Плоское поле – множество точек плоскости.

ственная точка второй фигуры и, наоборот, каждой точке второй фигуры соответствует единственная (прежняя) точка первой фигуры. Такое отображение называется изоморфизмом.

Отображение играет важную роль в начертательной геометрии, где изучают различные способы сопоставления абстрактных пространств и где под x и y понимают геометрические образы: точки, прямые, окружности и т.д.

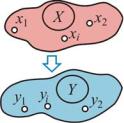
Рассмотрим два точечных множества X и Y (рис. 1). Каждой точке xi множества X ставится в соответствие единственная точка yi множества Y. Говорят, что X отображается на Y. Точка xi – прообраз точки yi, а yi – образ xi. Любая точка xi имеет единственный образ yi, но точка yi

может иметь несколько прообразов xi, xi1, xi2 и т. д. Выходит, что обратное соответствие x = f –1(y) в общем случае НЕОДНОЗНАЧНО. Отображение y = f(x) в одну сторону однозначно, а в другую – нет. Итак, отображение однозначно, когда каждому

элементу yi множества Y соответствует единственный прообраз множества X, т. е. прямое соответствие y = f(x) и обратное x = f –1(y) являются однозначными.

Есть ли взаимно однозначное соответствие между геометрическими образами при центральном и параллельном проецировании? Вернемся еще раз к рассмотрению центрального проецирования (рис. 2). Видим, что отмеченные точки А, В и С имеют свои проекции на плоскости П′, причем точка В находится за плоскостью, а точка С на самой плоскости (поэтому ее проекция C′ совпадает с самой точкой С).

Однако не для всех точек пространства могут быть найдены их центральные проекции. Так, для точки D проецирующий луч оказывается параллельным плоскости П′ и мы не в состоянии указать ее проекцию на П′. Точка D не является единственной: такой же особенностью расположения обладают все точки плоскости, проходящей через центр проекций параллельно плоскости проекций. Выходит, что не все точки пространства имеют свои проекции. Центральное проецирование имеет нарушение закономерности: не для всякой точки пространства можно построить ее проекцию на данную плоскость.

Как устранить это нарушение, этот «дефект»? Рассмотрим такую ситуацию. Пусть нужно спроецировать точки некоторой плоскости П на плоскость П′ из центра S (рис. 3).

Рис. 2

Рис. 3

Предположим, что точка А плоскости П спроецировалась в точку А′ плоскости П′, а точка В – в точку В′. Таким же способом могут быть найдены проекции бесчисленного множества точек плоскости П. Устанавливается взаимно однозначное соответствие между множеством точек плоскости П и множеством точек плоскости П′: каждой точке плоскости П соответствует единственная точка плоскости П′ (ее проекция) и наоборот. Но такое соответствие нарушается, если мы возьмем такую точку K плоскости П, что прямая SK будет параллельна плоскости П′. Это же относится ко всякой точке прямой l, проведенной в плоскости П параллельно плоскости П′. Точно так же мы не найдем соответствующей точки на плоскости П для точки М′ плоскости П′, если луч SМ′ параллелен плоскости П (а следовательно, и для всех точек прямой n′, лучи через которые проведены параллельно плоскости П).

Этот существенный недостаток центрального проецирования устраняется ДОПОЛНЕНИЕМ ЕВКЛИДОВА* ПРОСТРАНСТВА так называемыми «бесконечно удаленными» или «несобственными» элементами. Это делается следующим образом.

а) Две параллельные прямые считаются пересекающимися в несобственной точке. Следовательно, все прямые пространства, параллельные данной прямой, проходят через одну и ту же несобственную точку (имеем связку прямых с несобственным центром) (рис. 4).

Рис. 4

б) Совокупность несобственных точек данной плоскости считается несобственной прямой этой плоскости (рис. 5).

в) Две параллельные плоскости пересекаются по несобственной прямой. Следовательно, все плоскости пространства, параллельные данной плоскости, пересекаются по одной и той же несобственной прямой (рис. 6). Имеем

пучок плоскостей с несобственной осью.

* Евклидово пространство – пространство, изучаемое в элементарной геометрии. Названо в честь великого геометра древности, автора фундаментального труда по геометрии – Евклида.

Рис. 5

Рис. 6

г) Совокупность всех несобственных точек пространства считается несобственной плоскостью (трудно выразить графически).

Введенные дополнения делают центральное проецирование выполнимым для всех точек пространства без исключения.

Так, можно сказать, что прямая l (см. рис. 3) плоскости П проецируется в несобственную прямую l′ плоскости П′, а прямой n′ плоскости П′ соответствует несобственная прямая n плоскости П. При этом плоскость, образованная точкой S и прямой l, оказывается параллельной плоскости П′, а плоскость, образованная точкой S и прямой n′, – плоскости П.