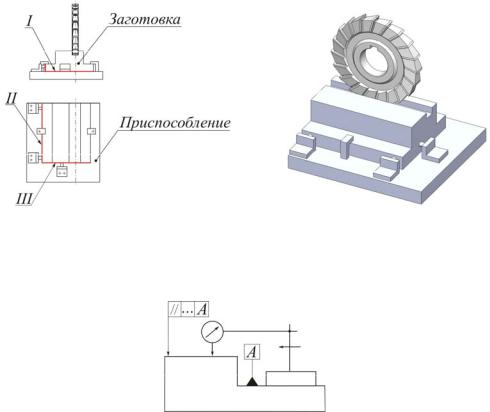
I, II, III – комплект технологических баз, определяющих положение заготовки в приспособлении

Рис. 10

A – измерительная база детали

Рис. 11

Различают и другие виды баз, например, базы по ограничению степеням свободы (установочные, направляющие, опорные и др.), или базы по характеру проявления (явные, скрытые).

1.3.2. КОЛИЧЕСТВО РАЗМЕРОВ ДЛЯ ПОЛНОГО ОПРЕДЕЛЕНИЯ ФОРМЫ ДЕТАЛЕЙ

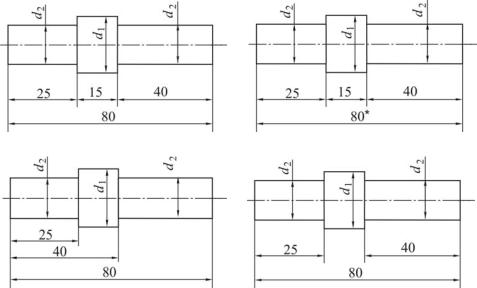
Для передачи всей полноты информации о форме детали необходимо определенное количество размеров, которое не зависит от того, как они будут заданы. От конструктора зависит выбор наиболее целесообразного варианта задания размеров. На рис. 12 показан валик, имеющий два соосных цилиндра вращения. Для его изготовления достаточно задать шесть размеров. Однако они могут быть заданы различным образом, и от конструктора зависит выбор

наиболее целесообразного варианта. Седьмой размер 80 на рис. 12, а только затрудняет понимание чертежа, так как становится неясным, от левого или правого торца надо отсчитывать размеры. Размерная цепь оказалась замкнутой. Если же размер 80 сделать справочным, для чего пометить его звездочкой (рис. 12, б), то такой вариант простановки будет правильным. Другие варианты (рис. 12, в, г) – тоже правильные, но они отвечают различным конструктивным и технологическим требованиям.

Рис. 12

Размер d2 проставлен дважды, поскольку если деталь имеет несколько одинаковых по форме и размерам элементов, в неясных случаях, например при отсутствии симметрии, размеры этих элементов повторяют. В других же случаях повторение размеров может привести к ошибкам, поэтому размер на чертеже наносят только один раз и на том изображении, где наиболее понятно, какую величину элемента этот размер указывает. Если бы валик был симмет-

ричным по форме, то диаметр d2 следовало бы указать один раз.

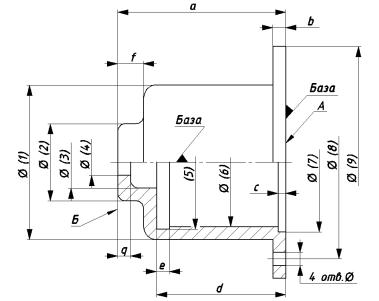
Правильный выбор баз – необходимое условие создания работоспособного изделия. На рис. 13 привалочная плоскость А и ось детали – конструкторские базы. От них отсчитывают размеры b, c, d, диаметры 1, 2 и т. д. Поверхность Б является вспомогательной (литейной) базой. От этой базы отсчитывается размер а до привалочной плоскости А.

Рис. 13

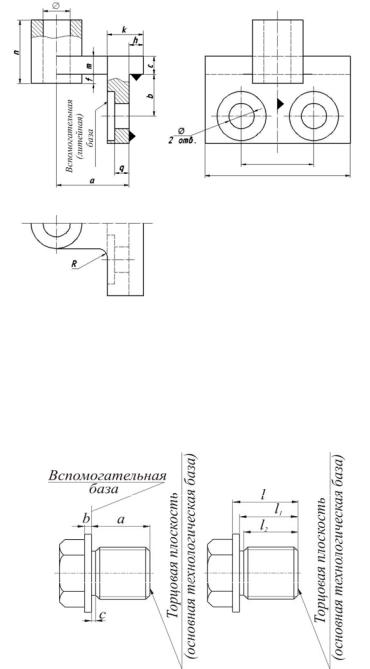
У детали, показанной на рис. 14, две плоскости и ось, условно отмеченные зачерненными треугольниками, – конструкторские базы. Сочетание поверхностей, образованных литьем и механической обработкой приводит к необходимости вводить еще одну вспомогательную конструкторскую базу (литейную), которая используется для изготовления литейной модели и приемки (контроля) отливки.

Согласно ГОСТ 2.307–68 на рабочих чертежах деталей, изготовляемых отливкой, штамповкой, ковкой или прокаткой с последующей механической обработкой части поверхности детали, указывают не более одного размера по каждому координатному направлению, связывающего механически обрабатываемые поверхности с поверхностями, не подвергаемыми механической обработке.

Размеры, определяющие литейную форму детали (отливки), проставляют от необрабатываемых поверхностей – литейных баз, от которых при обработке будут контролировать расстояния до конструкторских баз и проверять размеры на отливке. В горизонтальном направлении только один размер k проставлен от черной (литой) поверхности (вспомогательной конструкторской базы) до механически обрабатываемой поверхности. Все другие размеры в этом направлении проставлены только между механически обрабатываемыми поверхностями. В вертикальном направлении только один размер f связывает литую поверхность с нижним торцом прилива в виде втулки.

Рис. 14

Размеры некоторых элементов удобно отсчитывать от вспомогательных баз, ориентируя последние от основных. На рис. 15, а размеры b и c даны от вспомогательной базы. Вспомогательные базы вводят для того, чтобы при изготовлении деталей можно было проще контролировать и точнее определять заданные чертежом размеры без промежуточных замеров и вычислений. На рис. 15, б размеры заданы от одной базы, что неправильно.

а б Рис. 15

На рис. 16 показаны два варианта задания размеров конического отверстия. В первом варианте (рис. 16, а) глубина отверстия обусловлена подачей инструмента (сверла или зенкера). Данный вариант задания размера считается технологическим. В случае конструктивной необходимости этот размер заменяется размером диаметра основания конуса, полученного после обработки

(рис. 16, б).

Рис. 16

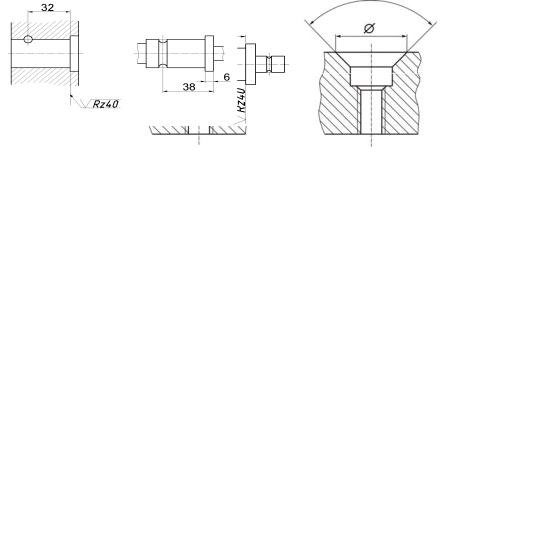
Назначение размеров с учетом только технологии изготовления не всегда может удовлетворять конструктивным требованиям. Так, на рис. 17, а приведен один из способов соединения ходового винта с подвижной частью слесарных тисков. Для отсчета сопрягаемого размера 32 на обеих деталях (рис. 17, б, в) выбрана поверхность, которая определяет взаимное положение деталей при работе. Задание сопрягаемого размера для этой канавки от правого торца кольцевого выступа, как показано на рис. 17, г, потребует задания уже не одного, а двух линейных размеров (38 и 6) с большей точностью, что усложнит технологический процесс изготовления, а следовательно, повысит стоимость детали.

Рис. 17