
- •ПРЕДИСЛОВИЕ
- •ВВЕДЕНИЕ
- •ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ИНЖЕНЕРНОЙ ГРАФИКИ
- •Элберт Хаббард
- •ПРИНЯТЫЕ ОБОЗНАЧЕНИЯ
- •ГЛАВА 1
- •ОСНОВНЫЕ ПОНЯТИЯ В ТЕОРИИ ИЗОБРАЖЕНИЯ ГЕОМЕТРИЧЕСКИХ ОБЪЕКТОВ
- •1. ЧТО ТАКОЕ НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ?
- •2. ГЕОМЕТРИЧЕСКОЕ МОДЕЛИРОВАНИЕ – ИНСТРУМЕНТ ПОЗНАНИЯ ДЕЙСТВИТЕЛЬНОСТИ
- •4. ПРОЕКЦИОННОЕ ОТОБРАЖЕНИЕ – АНАЛОГ ПОНЯТИЯ ФУНКЦИИ
- •Свойства центрального проецирования
- •Свойства параллельного проецирования
- •5. МЕТОД ДВУХ ИЗОБРАЖЕНИЙ
- •6. МОДЕЛЬ ТОЧКИ В ОРТОГОНАЛЬНЫХ ПРОЕКЦИЯХ
- •ВЫВОДЫ
- •ПРЯМАЯ ЛИНИЯ И ПЛОСКОСТЬ
- •1. ПОЛОЖЕНИЕ ПРЯМОЙ В ПРОСТРАНСТВЕ
- •3. ВЗАИМНОЕ ПОЛОЖЕНИЕ ДВУХ ПРЯМЫХ
- •4. ПОЛОЖЕНИЕ ПЛОСКОСТИ В ПРОСТРАНСТВЕ
- •5. РАСПОЛОЖЕНИЕ ПЛОСКОСТИ ОТНОСИТЕЛЬНО ОСНОВНЫХ ПЛОСКОСТЕЙ ПРОЕКЦИЙ
- •Проецирующая плоскость
- •Плоскость уровня
- •ВЫВОДЫ
- •УПРАЖНЕНИЕ
- •Задача № 1
- •Порядок выполнения
- •Задача № 2
- •Порядок выполнения
- •Задача № 3
- •Порядок выполнения
- •Задача № 4
- •Порядок выполнения
- •Задача № 5
- •Порядок выполнения
- •ГЛАВА 3
- •СПОСОБЫ ПРЕОБРАЗОВАНИЯ ПРОЕКЦИЙ
- •1. ПРИНАДЛЕЖНОСТЬ ПРЯМОЙ ЛИНИИ ПЛОСКОСТИ
- •1.1. ПРЯМАЯ ОБЩЕГО ПОЛОЖЕНИЯ В ПЛОСКОСТИ
- •1.2. ГЛАВНЫЕ ЛИНИИ ПЛОСКОСТИ
- •Линии уровня
- •Линии наибольшего наклона плоскости
- •2. СПОСОБЫ ПРЕОБРАЗОВАНИЯ ПРОЕКЦИЙ
- •2.1. ПЛОСКОПАРАЛЛЕЛЬНОЕ ПЕРЕМЕЩЕНИЕ
- •2.2. ВРАЩЕНИЕ ВОКРУГ ОСЕЙ, ПЕРПЕНДИКУЛЯРНЫХ ПЛОСКОСТЯМ ПРОЕКЦИЙ
- •2.3. ВРАЩЕНИЕ ВОКРУГ ОСЕЙ, ПАРАЛЛЕЛЬНЫХ ПЛОСКОСТЯМ ПРОЕКЦИЙ
- •2.4. ВРАЩЕНИЕ ВОКРУГ ОСЕЙ, ЛЕЖАЩИХ В ПЛОСКОСТЯХ ПРОЕКЦИЙ (СОВМЕЩЕНИЕ С ПЛОСКОСТЯМИ ПРОЕКЦИЙ)
- •2.5. ЗАМЕНА ПЛОСКОСТЕЙ ПРОЕКЦИЙ
- •ВЫВОДЫ
- •УПРАЖНЕНИЕ
- •ГЛАВА 4
- •ОБОБЩЕННЫЕ ПОЗИЦИОННЫЕ ЗАДАЧИ
- •1.1. ПРЯМАЯ ЛИНИЯ, ПАРАЛЛЕЛЬНАЯ ПЛОСКОСТИ
- •1.2. ПРЯМАЯ ЛИНИЯ, ПЕРЕСЕКАЮЩАЯ ПЛОСКОСТЬ (ОБЩИЙ СЛУЧАЙ)
- •1.3. ПРЯМАЯ ЛИНИЯ, ПЕРПЕНДИКУЛЯРНАЯ ПЛОСКОСТИ
- •2. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПЛОСКОСТЕЙ
- •2.1. ПЛОСКОСТИ ПАРАЛЛЕЛЬНЫЕ
- •2.2. ПЛОСКОСТИ ПЕРЕСЕКАЮЩИЕСЯ (ОБЩИЙ СЛУЧАЙ)
- •2.3. ПЛОСКОСТИ ВЗАИМНО ПЕРПЕНДИКУЛЯРНЫЕ
- •3. ВЗАИМНО ПЕРПЕНДИКУЛЯРНЫЕ ПРЯМЫЕ
- •4. ОБОБЩЕННЫЕ ПОЗИЦИОННЫЕ ЗАДАЧИ
- •4.1. ПЕРЕСЕЧЕНИЕ КРИВОЙ ЛИНИИ С ПОВЕРХНОСТЬЮ
- •4.2. ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ
- •4.3. ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА
- •ВЫВОДЫ
- •УПРАЖНЕНИЕ
- •Задача № 1
- •Порядок выполнения
- •Задача № 2
- •Порядок выполнения
- •Задача № 3
- •Порядок выполнения
- •Задача № 4
- •Порядок выполнения
- •Задача № 5
- •Порядок выполнения
- •ГЛАВА 5
- •1. ОБ АНАЛОГИИ МЕЖДУ ПОНЯТИЯМИ «ФУНКЦИЯ» И «ОТОБРАЖЕНИЕ»
- •2. ПЕРСПЕКТИВНАЯ КОЛЛИНЕАЦИЯ
- •Теорема Дезарга
- •Гомология
- •3. ПЕРСПЕКТИВНО-АФФИННОЕ (РОДСТВЕННОЕ) СООТВЕТСТВИЕ
- •4. СРАВНЕНИЕ ДВУХ ГОМОЛОГИЙ
- •ВЫВОДЫ
- •УПРАЖНЕНИЕ
- •Порядок выполнения
- •ГЛАВА 6
- •ПРОЕКЦИОННЫЕ МОДЕЛИ ТРЕХМЕРНЫХ ОБЪЕКТОВ
- •1. ВНЕШНЯЯ ФОРМА ПРЕДМЕТОВ И НЕОБХОДИМОСТЬ ВЫЯВЛЕНИЯ ИХ ВНУТРЕННИХ КОНТУРОВ
- •2. СИСТЕМЫ РАСПОЛОЖЕНИЯ ИЗОБРАЖЕНИЙ
- •3. ВИДЫ
- •3.1. ОСНОВНЫЕ ВИДЫ
- •3.2. ДОПОЛНИТЕЛЬНЫЕ ВИДЫ
- •3.3. МЕСТНЫЕ ВИДЫ
- •4. РАЗРЕЗЫ
- •4.1. ВИДЫ РАЗРЕЗОВ
- •4.2. ОБОЗНАЧЕНИЕ РАЗРЕЗОВ
- •5. СЕЧЕНИЯ
- •ВЫВОДЫ
- •УПРАЖНЕНИЕ
- •Задача № 1
- •Порядок выполнения
- •Задача № 2
- •Порядок выполнения
- •КРИВЫЕ ЛИНИИ
- •1. СПОСОБЫ ОБРАЗОВАНИЯ КРИВЫХ ЛИНИЙ
- •2. КЛАССИФИКАЦИЯ КРИВЫХ ЛИНИЙ
- •3. СПОСОБЫ ЗАДАНИЯ КРИВЫХ ЛИНИЙ
- •4. КАСАТЕЛЬНАЯ И НОРМАЛЬ К КРИВОЙ ЛИНИИ
- •5. УРАВНЕНИЯ КАСАТЕЛЬНОЙ И НОРМАЛИ
- •6. ВЕКТОР-ФУНКЦИЯ
- •7. КРИВИЗНА КРИВОЙ
- •8. КРУГ КРИВИЗНЫ
- •9. ЭВОЛЮТА И ЭВОЛЬВЕНТА
- •10. КРИВИЗНА ОКРУЖНОСТИ
- •11. КРИВЫЕ ЛИНИИ ВТОРОГО ПОРЯДКА
- •11.1. ЭЛЛИПС
- •11.2. ПАРАБОЛА
- •11.3. ГИПЕРБОЛА
- •12. КОНИЧЕСКИЕ СЕЧЕНИЯ
- •13. ПРОЕКЦИИ КРИВЫХ ЛИНИЙ
- •14. ЭЛЛИПС – ФИГУРА, РОДСТВЕННАЯ ОКРУЖНОСТИ
- •15. ОКРУЖНОСТЬ В ПЛОСКОСТИ ОБЩЕГО ПОЛОЖЕНИЯ
- •15.2. ОПРЕДЕЛЕНИЕ ВЕЛИЧИНЫ МАЛОЙ ОСИ ЭЛЛИПСА МЕТОДОМ ЗАМЕНЫ ПЛОСКОСТЕЙ ПРОЕКЦИЙ
- •15.3. ОПРЕДЕЛЕНИЕ ВЕЛИЧИНЫ МАЛОЙ ОСИ ЭЛЛИПСА С ПРИМЕНЕНИЕМ ЛИНИИ НАИБОЛЬШЕГО НАКЛОНА ПЛОСКОСТИ
- •ВЫВОДЫ
- •УПРАЖНЕНИЕ
- •Порядок выполнения
- •ГЛАВА 8
- •КРИВЫЕ ЛИНИИ, ИМЕЮЩИЕ ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ.
- •ОБВОДЫ ПРИ ПРОЕКТИРОВАНИИ ПОВЕРХНОСТЕЙ
- •1. НЕКОТОРЫЕ ПЛОСКИЕ КРИВЫЕ, ИМЕЮЩИЕ ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ
- •1.1. ЦИКЛИЧЕСКИЕ КРИВЫЕ
- •Циклоида
- •Эпициклоиды
- •Гипоциклоиды
- •1.2. СПИРАЛИ
- •1.3. ПОДЕРЫ
- •2.ПЛОСКИЕ СОСТАВНЫЕ КРИВЫЕ ЛИНИИ (ОБВОДЫ) ПРИ ПРОЕКТИРОВАНИИ ПОВЕРХНОСТЕЙ
- •2.1. АППРОКСИМАЦИЯ ТОЧЕЧНЫХ МАССИВОВ
- •2.3. ХАРАКТЕРНЫЕ ТОЧКИ КРИВЫХ
- •2.4. ПОРЯДОК ГЛАДКОСТИ ОБВОДОВ
- •2.5. ОСНОВНЫЕ СПОСОБЫ ПОСТРОЕНИЯ ОБВОДОВ
- •2.5.1. ИНТЕРПОЛЯЦИЯ ДУГАМИ ОКРУЖНОСТЕЙ
- •2.5.2. ИНТЕРПОЛЯЦИЯ КРИВЫМИ ВТОРОГО ПОРЯДКА
- •2.5.3. ИНТЕРПОЛЯЦИЯ ОБВОДОВ СПЛАЙН-ФУНКЦИЯМИ
- •ВЫВОДЫ
- •ГЛАВА 9
- •МНОГОГРАННЫЕ ПОВЕРХНОСТИ И МНОГОГРАННИКИ.
- •СИСТЕМАТИЗАЦИЯ ПОВЕРХНОСТЕЙ
- •1. МНОГОГРАННЫЕ ПОВЕРХНОСТИ
- •2. НЕКОТОРЫЕ ВИДЫ МНОГОГРАННИКОВ
- •3. ПЕРЕСЕЧЕНИЕ МНОГОГРАННИКА ПЛОСКОСТЬЮ
- •5. ВЗАИМНОЕ ПЕРЕСЕЧЕНИЕ МНОГОГРАННИКОВ
- •6. РАЗВЕРТКИ МНОГОГРАННИКОВ
- •6.1. СПОСОБ НОРМАЛЬНОГО СЕЧЕНИЯ
- •6.2. СПОСОБ РАСКАТКИ
- •6.3. СПОСОБ ТРЕУГОЛЬНИКОВ (ТРИАНГУЛЯЦИИ)
- •7. СИСТЕМАТИЗАЦИЯ ПОВЕРХНОСТЕЙ
- •ВЫВОДЫ
- •УПРАЖНЕНИЕ
- •Порядок выполнения
- •СЛОЖНЫЕ ПОВЕРХНОСТИ
- •1. ОПРЕДЕЛЕНИЕ ПОВЕРХНОСТИ
- •2. СПОСОБЫ ОБРАЗОВАНИЯ ПОВЕРХНОСТЕЙ
- •2.1. ОБРАЗОВАНИЕ ПОВЕРХНОСТЕЙ ПРИ ПОМОЩИ ДВИЖУЩЕЙСЯ ЛИНИИ
- •2.2. ОБРАЗОВАНИЕ ПОВЕРХНОСТЕЙ ПРИ ПОМОЩИ ДВИЖУЩЕЙСЯ ПОВЕРХНОСТИ
- •3. СПОСОБЫ ЗАДАНИЯ ПОВЕРХНОСТЕЙ
- •3.1. ГРАФИЧЕСКИЙ СПОСОБ ЗАДАНИЯ КИНЕМАТИЧЕСКИХ ПОВЕРХНОСТЕЙ
- •3.2. АНАЛИТИЧЕСКИЙ СПОСОБ ЗАДАНИЯ ПОВЕРХНОСТЕЙ
- •3.3. ПРИМЕР АНАЛИТИЧЕСКОГО СПОСОБА ЗАДАНИЯ ПОВЕРХНОСТИ
- •4. ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ ПОВЕРХНОСТЕЙ
- •4.1. ТРЕХГРАННИК ФРЕНЕ
- •4.2. ЕСТЕСТВЕННЫЕ КООРДИНАТЫ ПРОСТРАНСТВЕННОЙ КРИВОЙ
- •5. КРИВЫЕ ЛИНИИ НА СФЕРЕ
- •6. КАСАТЕЛЬНЫЕ И НОРМАЛИ К ПОВЕРХНОСТИ ПРИ ОБРАБОТКЕ ЕЕ НА СТАНКАХ С ЧПУ
- •7.2. КАРКАСНО-КИНЕМАТИЧЕСКИЙ МЕТОД ПРОЕКТИРОВАНИЯ
- •ВЫВОДЫ
- •УПРАЖНЕНИЕ
- •Порядок выполнения
- •ПОВЕРХНОСТИ ВРАЩЕНИЯ И ВИНТОВЫЕ
- •1. ПОВЕРХНОСТИ ВРАЩЕНИЯ
- •3. ПРИМЕРЫ ПОВЕРХНОСТЕЙ ВРАЩЕНИЯ
- •3.1. СФЕРА
- •3.2. ЦИЛИНДР ВРАЩЕНИЯ
- •3.3. КОНУС ВРАЩЕНИЯ
- •3.4. ГИПЕРБОЛОИД ВРАЩЕНИЯ
- •4. ВИНТОВЫЕ ПОВЕРХНОСТИ
- •4.1. ПРЯМОЙ ГЕЛИКОИД
- •4.2. ДРУГИЕ ВИДЫ ВИНТОВЫХ ПОВЕРХНОСТЕЙ
- •ВЫВОДЫ
- •УПРАЖНЕНИЕ
- •Порядок выполнения
- •ЛИНЕЙЧАТЫЕ ПОВЕРХНОСТИ
- •1. СПОСОБ ОБРАЗОВАНИЯ ПОВЕРХНОСТЕЙ ДВИЖЕНИЕМ ПРЯМОЙ ЛИНИИ
- •2.1. КОНИЧЕСКИЕ ПОВЕРХНОСТИ
- •2.2. ЦИЛИНДРИЧЕСКИЕ ПОВЕРХНОСТИ
- •3. ЛИНЕЙЧАТЫЕ ПОВЕРХНОСТИ
- •3.1. ЦИЛИНДРОИД
- •3.2. КОНОИД
- •3.3. ГИПЕРБОЛИЧЕСКИЙ ПАРАБОЛОИД (КОСАЯ ПЛОСКОСТЬ)
- •ВЫВОДЫ
- •УПРАЖНЕНИЕ
- •Порядок выполнения
- •ГЛАВА 13
- •РАЗВЕРТКИ ПОВЕРХНОСТЕЙ
- •1. ПЛОСКОСТЬ, КАСАТЕЛЬНАЯ К ПОВЕРХНОСТИ
- •1.1. ОСНОВНЫЕ ПОНЯТИЯ
- •1.2. ПОСТРОЕНИЕ КАСАТЕЛЬНОЙ ПЛОСКОСТИ
- •2. РАЗВЕРТКИ ПОВЕРХНОСТЕЙ
- •2.1. ПОРЯДОК ПОСТРОЕНИЯ РАЗВЕРТОК В ОБЩЕМ СЛУЧАЕ
- •2.2. ОСНОВНЫЕ СВОЙСТВА РАЗВЕРТЫВАЮЩИХСЯ ПОВЕРХНОСТЕЙ
- •2.3. ПРИМЕРЫ РАЗВЕРТЫВАНИЯ КРИВЫХ ПОВЕРХНОСТЕЙ
- •Прямой круговой цилиндр
- •Наклонный цилиндр
- •Конус
- •2.4. РАЗВЕРТКИ НЕРАЗВЕРТЫВАЮЩИХСЯ ПОВЕРХНОСТЕЙ
- •ВЫВОДЫ
- •УПРАЖНЕНИЕ
- •Задача № 1
- •Порядок выполнения
- •Задача № 2
- •Порядок выполнения
- •Задача № 3
- •Порядок выполнения
- •Создание конуса с вырезом
- •Создание развертки
- •Задача № 4
- •Порядок выполнения
- •АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ
- •1. ОСНОВНЫЕ ПОНЯТИЯ
- •2. СУТЬ СПОСОБА ПОЛУЧЕНИЯ АКСОНОМЕТРИЧЕСКИХ ПРОЕКЦИЙ
- •5. СТАНДАРТНЫЕ ВИДЫ АКСОНОМЕТРИЧЕСКИХ ПРОЕКЦИЙ
- •5.1. ПРЯМОУГОЛЬНАЯ ИЗОМЕТРИЯ
- •5.1.1. ОКРУЖНОСТЬ В ПРЯМОУГОЛЬНОЙ ИЗОМЕТРИИ
- •5.2. ПРЯМОУГОЛЬНАЯ ДИМЕТРИЯ
- •6. КОСОУГОЛЬНЫЕ АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ
- •6.1. ФРОНТАЛЬНАЯ ИЗОМЕТРИЧЕСКАЯ ПРОЕКЦИЯ
- •6.2. ГОРИЗОНТАЛЬНАЯ ИЗОМЕТРИЧЕСКАЯ ПРОЕКЦИЯ
- •6.3. ФРОНТАЛЬНАЯ ДИМЕТРИЧЕСКАЯ ПРОЕКЦИЯ
- •ВЫВОДЫ
- •ГЛАВА 15
- •1. ПАРАМЕТРИЗАЦИЯ МАКРОГЕОМЕТРИИ ПОВЕРХНОСТЕЙ ТЕХНИЧЕСКИХ ИЗДЕЛИЙ
- •1.3. ЗАДАНИЕ РАЗМЕРОВ
- •1.3.1. БАЗИРОВАНИЕ И БАЗЫ
- •1.3.2. КОЛИЧЕСТВО РАЗМЕРОВ ДЛЯ ПОЛНОГО ОПРЕДЕЛЕНИЯ ФОРМЫ ДЕТАЛЕЙ
- •1.3.3. РАЗМЕРЫ ФОРМЫ И РАЗМЕРЫ ПОЛОЖЕНИЯ ПОВЕРХНОСТЕЙ
- •1.3.4. КОНСТРУКТИВНАЯ НЕОПРЕДЕЛЕННОСТЬ БАЗ
- •1.4. НАНЕСЕНИЕ РАЗМЕРОВ
- •1.5. ОСЕВЫЕ И ЦЕНТРОВЫЕ ЛИНИИ
- •2. ПАРАМЕТРИЗАЦИЯ МИКРОГЕОМЕТРИИ ПОВЕРХНОСТЕЙ ТЕХНИЧЕСКИХ ИЗДЕЛИЙ
- •ВЫВОДЫ
- •УПРАЖНЕНИЕ
- •Задача № 1
- •Задача № 2
- •Порядок выполнения
- •ЗАКЛЮЧЕНИЕ
- •БИБЛИОГРАФИЧЕСКИЙ СПИСОК
- •ОГЛАВЛЕНИЕ

330 |
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ИНЖЕНЕРНОЙ ГРАФИКИ |
5.2.ПРЯМОУГОЛЬНАЯ ДИМЕТРИЯ
Вто время как прямоугольная изометрия существует только одна, прямоугольных диметрий можно построить бесчисленное множество. Наиболее простую и распространенную диметрию получают, если
u = w и v = u2 .
Вычислим показатели искажений по осям. Из уравнения u2 + v2 + w2 = 2 имеем:
u2 + u2 +u2 = 2 , 4
откуда
u = 2 32 ≈ 0,94 ,
тогда
u = w = 0, 94; v = u2 = ≈ 0,942 ≈ 0, 47 .
Итак, диметрический масштаб измерения по двум осям x′ и z′ равен ≈ 0,94, а по оси y′ равен ≈ 0,47, т. е. по аксонометрическим осям происходит
сокращение размеров на эти величины.
На практике пользуются приведенными показателями искажения: вместо 0,94 принимают 1, а вместо 0,47 – 0,5. Тогда изображение становится увеличенным в 1,06 раза по сравнению с диметрией, построенной с помощью точ-
ных показателей искажения |
1 |
= |
0,5 |
=1, 06 . |
|
0,94 |
0, 47 |
||||
|
|
|
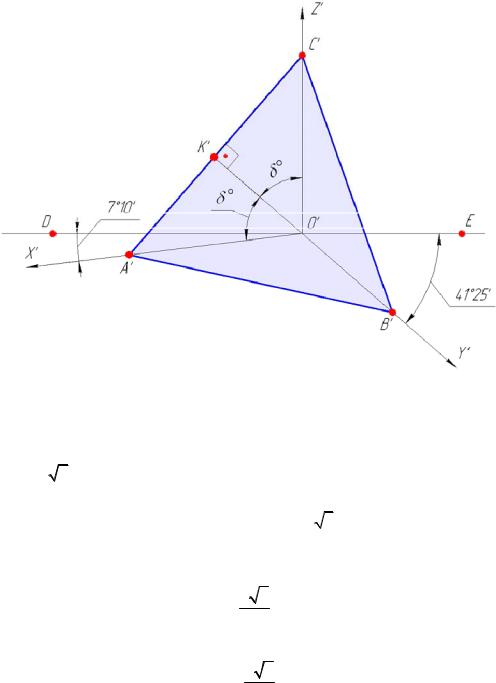
Определим углы между осями прямоугольной диметрии, для чего воспользуемся треугольником следов A′ B′ C′ (рис. 12). Так как из-за равенства показателей искажения по осям x′и z′ он – равнобедренный, то его высота является в то же время и медианой, т. е. A′K′= K′ C′. Из прямоугольного треугольника O′ K′ C′ имеем:
sin δ = OK′′CC′′ = 2AO′C′C′′ , так как K′C′ = 12 A′C′.
Г л а в а 14. Аксонометрические проекции |
331 |
Рис. 12
Чтобы определить это соотношение, выразим оба его члена через отрезок
OC |
′ |
натуральной координатной оси z. Равнобедренный треугольник |
′ ′ ′ |
|||||||||
|
A O C |
|||||||||||
является проекцией прямоугольного треугольника |
|
′ |
′ |
(см. рис. 5), поэтому |
||||||||
A OC |
|
|||||||||||
′ ′ |
= OC |
′ |
2 . |
|
|
|
|
|
|
|
|
|
A C |
|
|
|
|
|
|
|
|
|
|||
Далее имеем |
|
|
|
|
|
|
|
|
||||
|
|
|
|
′ ′ |
′ |
, но ω= |
2 |
2 |
. |
|
|
|
|
|
|
|
3 |
|
|
|
|||||
|
|
|
|
O C |
= ω OC |
|
|
|
||||
Поэтому
O′C′ = 2 32 OC′,
откуда
2O′C′ = 4 32 OC′.
332 |
|
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ИНЖЕНЕРНОЙ ГРАФИКИ |
|||||||||
Следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
2 |
|
|
3 |
|
|
|
|
|
sin δ = (OC′ |
2) |
: |
|
|
OC′ |
= |
4 |
= 0,75. |
|
|
|
|
3 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||
что соответствует равенству угла δ° |
|
′ |
. Тогда угол |
′ ′ |
′ |
равняется |
|||||
= 48°35 |
A O C |
|
|||||||||
двум углам δ°, т. е. 97°10′.
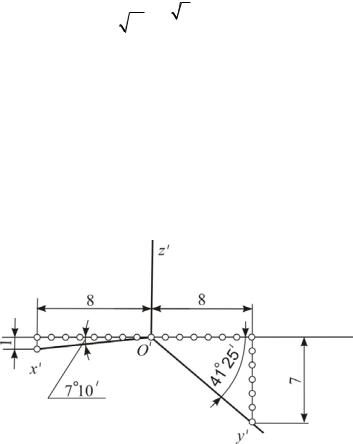
Обычно ось z′ при построении диметрических проекций располагают вертикально, тогда треугольник следов и его высоты (аксонометрические оси)
займут положение, |
показанное |
на |
рис. 12. В этом |
|
случае угол |
′ ′ |
= |
||||
|
DO A |
||||||||||
′ |
|
′ |
′ |
|
′ |
|
′ |
′ |
′ |
′ |
|
= (97°10 |
−90°) = 7°10 , угол |
DO K |
|
= (δ−7°10 ) = (48°35 |
−7°10 ) = 41°25 . |
|
|||||
Расположение аксонометрических осей показано на рис. 13: ось z′ – вертикально, ось x′ составляет с горизонтальной линией угол 7°10′ , а ось y′ –
41°25′.
Рис. 13
Углы между осями можно брать из соотношения катетов прямоугольных треугольников, гипотенузы которых указывают направление осей. Так,
′ |
= |
1 |
; |
′ |
= |
7 |
tg 7°10 |
8 |
tg 41°25 |
8 . |
При построении точной прямоугольной диметрии значения координат по направлению осей x′ и z′ умножают на величину 0,94, а по оси y′ – на величи-
ну 0,47.
На практике пользуются ПРИВЕДЕННЫМИ показателями искажений, равными 1 и 0,5, при этом все элементы изображения увеличиваются в 1/0,94 = = 1,06 раза.
Г л а в а 14. Аксонометрические проекции |
333 |
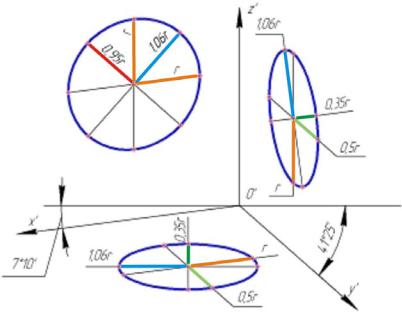
На рис. 14 показаны три эллипса, изображающие окружности, расположенные в плоскостях, параллельных координатным плоскостям в прямоугольной диметрии.
Рис. 14
В диметрии, так же как в изометрии, большие оси эллипсов перпендикулярны осям, отсутствующим в плоскости изображаемой окружности, а малые имеют направления аксонометрических осей. В натуральной диметрии большие оси эллипсов равны диаметру d окружности, а в приведенной они равны 1,06d. На рис. 14 указаны размеры осей эллипсов с учетом приведенных показателей искажения.
На практике часто эллипсы заменяют овалами. Для их построения в плоскостях xOy и yOz (и им параллельных) проводят большие и малые оси
D = AB =1, 06d и d |
|
= СD = |
1 |
D |
|
, затем на продолжении малой оси от точ- |
|
0 |
|
|
|||||
|
0 |
3 |
0 |
|
|||
|
|
|
|
|
|
||
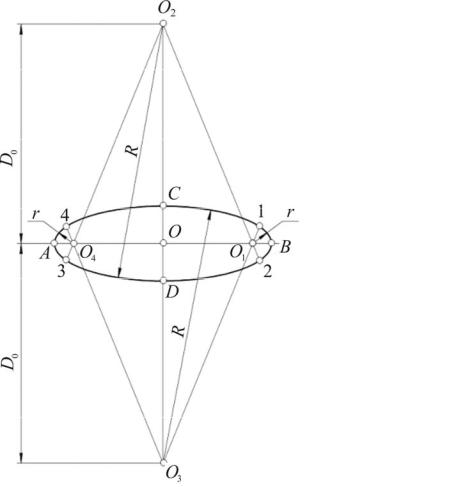
ки О в ту и другую стороны откладывают размер D0, получая центры О2 и О3 (рис. 15). Из этих центров через точки С и D проводят дуги радиусом
R = D0 + 12 d0 .
334 |
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ИНЖЕНЕРНОЙ ГРАФИКИ |
Из центров О1 и О4, отстоящих от концов А и В большой оси на расстоянии
14 d0, проводят дуги радиусом r. Эти дуги доводят до точек сопряжения 1 и 2, 3 и 4, полученных на продолжении линии центров сопрягаемых дуг.
АВ z или AB x AB = D0 = 1,06d
1
СD = d0 = 3 D0 = 0,35d
1
R = D0 + 2 d0
1
r = 4 d0
d – диаметр окружности
Рис. 15
Для построения овала, расположенного в плоскости xOz (или в плоскости, параллельной ей), проводят прямую, перпендикулярную оси y, отсутствующей в данной плоскости (рис. 16). На этой прямой откладывают величину большой
оси D0 = АВ. Малую ось d0 = СD откладывают на прямой, совпадающей
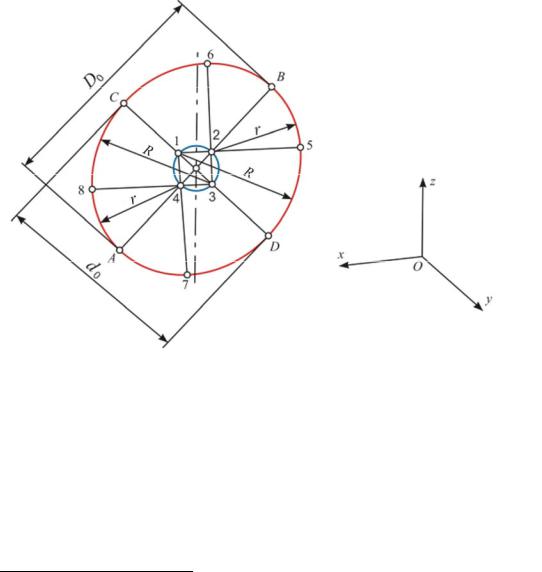
Г л а в а 14. Аксонометрические проекции |
335 |
снаправлением оси y, перпендикулярной АВ. Из точки пересечения большой
ималой осей проводят окружность диаметра d1 = 0,2d, получая центры 1, 2, 3 и 4. Из центров 1 и 3 проводят дуги радиусом R, а из центров 2 и 4 – дуги радиусом r. Дуги радиусами R и r доводят до точек сопряжения 5 и 6, полученных на продолжении линии центров сопрягаемых дуг.
АВ y
AB = D0 = 1,06d
СD = d0 = 0,94d
d – диаметр окружности
Рис. 16
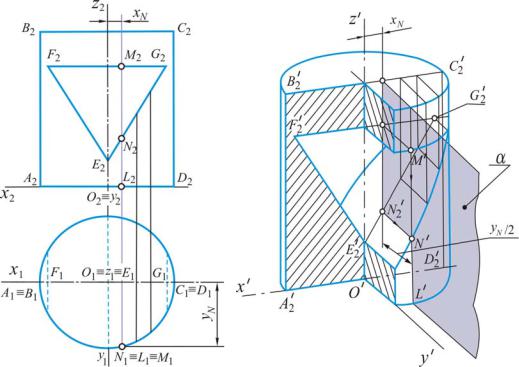
Пример. Построить прямоугольную диметрию цилиндра со сквозным отверстием треугольной формы (рис. 17)*.
Начало координат совместим с центром нижнего основания, а ось z c осью цилиндра. В данном случае вторичную проекцию целесообразно построить на координатной плоскости x′O′z′ , поскольку для этого потребуется провести только прямые линии. Такой проекцией служит параллелограмм A2′B2′C2′D2′ и
треугольник E2′F2′G2′ . Для того чтобы придать чертежу большую наглядность, цилиндр изобразим с вырезом одной четверти.
* Пример приведен из работы [19].
336 |
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ИНЖЕНЕРНОЙ ГРАФИКИ |
Рис. 17
Не останавливаясь на вычерчивании эллипсов – контуров верхнего и нижнего оснований цилиндра, рассмотрим построение одной из точек N′ эллиптической дуги, по которой наклонная плоскость треугольного отверстия пересекает цилиндрическую поверхность.
Аксонометрическую проекцию N′ точки N можно найти как с помощью ортогонального чертежа, так и независимо от него. В первом случае на ортогональных проекциях определяем две прямоугольные координаты xN и yN
этой точки. Затем с помощью координаты xN на прямой E2′G2′ показываем вторичную проекцию N2′ . Наконец, через N2′ проводим прямую, параллельную оси y′, и откладываем на ней от точки N2′ отрезок, равный 0,5 yN . Дру-
гими словами, N′ строим способом координат.
Та же точка может быть определена пересечением образующей L′M ′ цилиндра и горизонтали N2′N′ наклонной плоскости отверстия, причем и обра-
зующая, и горизонталь должны принадлежать одной плоскости α, параллельной координатной плоскости y′O′z′. На рис. 17 аналогично найдены и осталь-
ные точки кривой наклонного сечения.
