
- •ПРЕДИСЛОВИЕ
- •ВВЕДЕНИЕ
- •ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ИНЖЕНЕРНОЙ ГРАФИКИ
- •Элберт Хаббард
- •ПРИНЯТЫЕ ОБОЗНАЧЕНИЯ
- •ГЛАВА 1
- •ОСНОВНЫЕ ПОНЯТИЯ В ТЕОРИИ ИЗОБРАЖЕНИЯ ГЕОМЕТРИЧЕСКИХ ОБЪЕКТОВ
- •1. ЧТО ТАКОЕ НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ?
- •2. ГЕОМЕТРИЧЕСКОЕ МОДЕЛИРОВАНИЕ – ИНСТРУМЕНТ ПОЗНАНИЯ ДЕЙСТВИТЕЛЬНОСТИ
- •4. ПРОЕКЦИОННОЕ ОТОБРАЖЕНИЕ – АНАЛОГ ПОНЯТИЯ ФУНКЦИИ
- •Свойства центрального проецирования
- •Свойства параллельного проецирования
- •5. МЕТОД ДВУХ ИЗОБРАЖЕНИЙ
- •6. МОДЕЛЬ ТОЧКИ В ОРТОГОНАЛЬНЫХ ПРОЕКЦИЯХ
- •ВЫВОДЫ
- •ПРЯМАЯ ЛИНИЯ И ПЛОСКОСТЬ
- •1. ПОЛОЖЕНИЕ ПРЯМОЙ В ПРОСТРАНСТВЕ
- •3. ВЗАИМНОЕ ПОЛОЖЕНИЕ ДВУХ ПРЯМЫХ
- •4. ПОЛОЖЕНИЕ ПЛОСКОСТИ В ПРОСТРАНСТВЕ
- •5. РАСПОЛОЖЕНИЕ ПЛОСКОСТИ ОТНОСИТЕЛЬНО ОСНОВНЫХ ПЛОСКОСТЕЙ ПРОЕКЦИЙ
- •Проецирующая плоскость
- •Плоскость уровня
- •ВЫВОДЫ
- •УПРАЖНЕНИЕ
- •Задача № 1
- •Порядок выполнения
- •Задача № 2
- •Порядок выполнения
- •Задача № 3
- •Порядок выполнения
- •Задача № 4
- •Порядок выполнения
- •Задача № 5
- •Порядок выполнения
- •ГЛАВА 3
- •СПОСОБЫ ПРЕОБРАЗОВАНИЯ ПРОЕКЦИЙ
- •1. ПРИНАДЛЕЖНОСТЬ ПРЯМОЙ ЛИНИИ ПЛОСКОСТИ
- •1.1. ПРЯМАЯ ОБЩЕГО ПОЛОЖЕНИЯ В ПЛОСКОСТИ
- •1.2. ГЛАВНЫЕ ЛИНИИ ПЛОСКОСТИ
- •Линии уровня
- •Линии наибольшего наклона плоскости
- •2. СПОСОБЫ ПРЕОБРАЗОВАНИЯ ПРОЕКЦИЙ
- •2.1. ПЛОСКОПАРАЛЛЕЛЬНОЕ ПЕРЕМЕЩЕНИЕ
- •2.2. ВРАЩЕНИЕ ВОКРУГ ОСЕЙ, ПЕРПЕНДИКУЛЯРНЫХ ПЛОСКОСТЯМ ПРОЕКЦИЙ
- •2.3. ВРАЩЕНИЕ ВОКРУГ ОСЕЙ, ПАРАЛЛЕЛЬНЫХ ПЛОСКОСТЯМ ПРОЕКЦИЙ
- •2.4. ВРАЩЕНИЕ ВОКРУГ ОСЕЙ, ЛЕЖАЩИХ В ПЛОСКОСТЯХ ПРОЕКЦИЙ (СОВМЕЩЕНИЕ С ПЛОСКОСТЯМИ ПРОЕКЦИЙ)
- •2.5. ЗАМЕНА ПЛОСКОСТЕЙ ПРОЕКЦИЙ
- •ВЫВОДЫ
- •УПРАЖНЕНИЕ
- •ГЛАВА 4
- •ОБОБЩЕННЫЕ ПОЗИЦИОННЫЕ ЗАДАЧИ
- •1.1. ПРЯМАЯ ЛИНИЯ, ПАРАЛЛЕЛЬНАЯ ПЛОСКОСТИ
- •1.2. ПРЯМАЯ ЛИНИЯ, ПЕРЕСЕКАЮЩАЯ ПЛОСКОСТЬ (ОБЩИЙ СЛУЧАЙ)
- •1.3. ПРЯМАЯ ЛИНИЯ, ПЕРПЕНДИКУЛЯРНАЯ ПЛОСКОСТИ
- •2. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПЛОСКОСТЕЙ
- •2.1. ПЛОСКОСТИ ПАРАЛЛЕЛЬНЫЕ
- •2.2. ПЛОСКОСТИ ПЕРЕСЕКАЮЩИЕСЯ (ОБЩИЙ СЛУЧАЙ)
- •2.3. ПЛОСКОСТИ ВЗАИМНО ПЕРПЕНДИКУЛЯРНЫЕ
- •3. ВЗАИМНО ПЕРПЕНДИКУЛЯРНЫЕ ПРЯМЫЕ
- •4. ОБОБЩЕННЫЕ ПОЗИЦИОННЫЕ ЗАДАЧИ
- •4.1. ПЕРЕСЕЧЕНИЕ КРИВОЙ ЛИНИИ С ПОВЕРХНОСТЬЮ
- •4.2. ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ
- •4.3. ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА
- •ВЫВОДЫ
- •УПРАЖНЕНИЕ
- •Задача № 1
- •Порядок выполнения
- •Задача № 2
- •Порядок выполнения
- •Задача № 3
- •Порядок выполнения
- •Задача № 4
- •Порядок выполнения
- •Задача № 5
- •Порядок выполнения
- •ГЛАВА 5
- •1. ОБ АНАЛОГИИ МЕЖДУ ПОНЯТИЯМИ «ФУНКЦИЯ» И «ОТОБРАЖЕНИЕ»
- •2. ПЕРСПЕКТИВНАЯ КОЛЛИНЕАЦИЯ
- •Теорема Дезарга
- •Гомология
- •3. ПЕРСПЕКТИВНО-АФФИННОЕ (РОДСТВЕННОЕ) СООТВЕТСТВИЕ
- •4. СРАВНЕНИЕ ДВУХ ГОМОЛОГИЙ
- •ВЫВОДЫ
- •УПРАЖНЕНИЕ
- •Порядок выполнения
- •ГЛАВА 6
- •ПРОЕКЦИОННЫЕ МОДЕЛИ ТРЕХМЕРНЫХ ОБЪЕКТОВ
- •1. ВНЕШНЯЯ ФОРМА ПРЕДМЕТОВ И НЕОБХОДИМОСТЬ ВЫЯВЛЕНИЯ ИХ ВНУТРЕННИХ КОНТУРОВ
- •2. СИСТЕМЫ РАСПОЛОЖЕНИЯ ИЗОБРАЖЕНИЙ
- •3. ВИДЫ
- •3.1. ОСНОВНЫЕ ВИДЫ
- •3.2. ДОПОЛНИТЕЛЬНЫЕ ВИДЫ
- •3.3. МЕСТНЫЕ ВИДЫ
- •4. РАЗРЕЗЫ
- •4.1. ВИДЫ РАЗРЕЗОВ
- •4.2. ОБОЗНАЧЕНИЕ РАЗРЕЗОВ
- •5. СЕЧЕНИЯ
- •ВЫВОДЫ
- •УПРАЖНЕНИЕ
- •Задача № 1
- •Порядок выполнения
- •Задача № 2
- •Порядок выполнения
- •КРИВЫЕ ЛИНИИ
- •1. СПОСОБЫ ОБРАЗОВАНИЯ КРИВЫХ ЛИНИЙ
- •2. КЛАССИФИКАЦИЯ КРИВЫХ ЛИНИЙ
- •3. СПОСОБЫ ЗАДАНИЯ КРИВЫХ ЛИНИЙ
- •4. КАСАТЕЛЬНАЯ И НОРМАЛЬ К КРИВОЙ ЛИНИИ
- •5. УРАВНЕНИЯ КАСАТЕЛЬНОЙ И НОРМАЛИ
- •6. ВЕКТОР-ФУНКЦИЯ
- •7. КРИВИЗНА КРИВОЙ
- •8. КРУГ КРИВИЗНЫ
- •9. ЭВОЛЮТА И ЭВОЛЬВЕНТА
- •10. КРИВИЗНА ОКРУЖНОСТИ
- •11. КРИВЫЕ ЛИНИИ ВТОРОГО ПОРЯДКА
- •11.1. ЭЛЛИПС
- •11.2. ПАРАБОЛА
- •11.3. ГИПЕРБОЛА
- •12. КОНИЧЕСКИЕ СЕЧЕНИЯ
- •13. ПРОЕКЦИИ КРИВЫХ ЛИНИЙ
- •14. ЭЛЛИПС – ФИГУРА, РОДСТВЕННАЯ ОКРУЖНОСТИ
- •15. ОКРУЖНОСТЬ В ПЛОСКОСТИ ОБЩЕГО ПОЛОЖЕНИЯ
- •15.2. ОПРЕДЕЛЕНИЕ ВЕЛИЧИНЫ МАЛОЙ ОСИ ЭЛЛИПСА МЕТОДОМ ЗАМЕНЫ ПЛОСКОСТЕЙ ПРОЕКЦИЙ
- •15.3. ОПРЕДЕЛЕНИЕ ВЕЛИЧИНЫ МАЛОЙ ОСИ ЭЛЛИПСА С ПРИМЕНЕНИЕМ ЛИНИИ НАИБОЛЬШЕГО НАКЛОНА ПЛОСКОСТИ
- •ВЫВОДЫ
- •УПРАЖНЕНИЕ
- •Порядок выполнения
- •ГЛАВА 8
- •КРИВЫЕ ЛИНИИ, ИМЕЮЩИЕ ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ.
- •ОБВОДЫ ПРИ ПРОЕКТИРОВАНИИ ПОВЕРХНОСТЕЙ
- •1. НЕКОТОРЫЕ ПЛОСКИЕ КРИВЫЕ, ИМЕЮЩИЕ ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ
- •1.1. ЦИКЛИЧЕСКИЕ КРИВЫЕ
- •Циклоида
- •Эпициклоиды
- •Гипоциклоиды
- •1.2. СПИРАЛИ
- •1.3. ПОДЕРЫ
- •2.ПЛОСКИЕ СОСТАВНЫЕ КРИВЫЕ ЛИНИИ (ОБВОДЫ) ПРИ ПРОЕКТИРОВАНИИ ПОВЕРХНОСТЕЙ
- •2.1. АППРОКСИМАЦИЯ ТОЧЕЧНЫХ МАССИВОВ
- •2.3. ХАРАКТЕРНЫЕ ТОЧКИ КРИВЫХ
- •2.4. ПОРЯДОК ГЛАДКОСТИ ОБВОДОВ
- •2.5. ОСНОВНЫЕ СПОСОБЫ ПОСТРОЕНИЯ ОБВОДОВ
- •2.5.1. ИНТЕРПОЛЯЦИЯ ДУГАМИ ОКРУЖНОСТЕЙ
- •2.5.2. ИНТЕРПОЛЯЦИЯ КРИВЫМИ ВТОРОГО ПОРЯДКА
- •2.5.3. ИНТЕРПОЛЯЦИЯ ОБВОДОВ СПЛАЙН-ФУНКЦИЯМИ
- •ВЫВОДЫ
- •ГЛАВА 9
- •МНОГОГРАННЫЕ ПОВЕРХНОСТИ И МНОГОГРАННИКИ.
- •СИСТЕМАТИЗАЦИЯ ПОВЕРХНОСТЕЙ
- •1. МНОГОГРАННЫЕ ПОВЕРХНОСТИ
- •2. НЕКОТОРЫЕ ВИДЫ МНОГОГРАННИКОВ
- •3. ПЕРЕСЕЧЕНИЕ МНОГОГРАННИКА ПЛОСКОСТЬЮ
- •5. ВЗАИМНОЕ ПЕРЕСЕЧЕНИЕ МНОГОГРАННИКОВ
- •6. РАЗВЕРТКИ МНОГОГРАННИКОВ
- •6.1. СПОСОБ НОРМАЛЬНОГО СЕЧЕНИЯ
- •6.2. СПОСОБ РАСКАТКИ
- •6.3. СПОСОБ ТРЕУГОЛЬНИКОВ (ТРИАНГУЛЯЦИИ)
- •7. СИСТЕМАТИЗАЦИЯ ПОВЕРХНОСТЕЙ
- •ВЫВОДЫ
- •УПРАЖНЕНИЕ
- •Порядок выполнения
- •СЛОЖНЫЕ ПОВЕРХНОСТИ
- •1. ОПРЕДЕЛЕНИЕ ПОВЕРХНОСТИ
- •2. СПОСОБЫ ОБРАЗОВАНИЯ ПОВЕРХНОСТЕЙ
- •2.1. ОБРАЗОВАНИЕ ПОВЕРХНОСТЕЙ ПРИ ПОМОЩИ ДВИЖУЩЕЙСЯ ЛИНИИ
- •2.2. ОБРАЗОВАНИЕ ПОВЕРХНОСТЕЙ ПРИ ПОМОЩИ ДВИЖУЩЕЙСЯ ПОВЕРХНОСТИ
- •3. СПОСОБЫ ЗАДАНИЯ ПОВЕРХНОСТЕЙ
- •3.1. ГРАФИЧЕСКИЙ СПОСОБ ЗАДАНИЯ КИНЕМАТИЧЕСКИХ ПОВЕРХНОСТЕЙ
- •3.2. АНАЛИТИЧЕСКИЙ СПОСОБ ЗАДАНИЯ ПОВЕРХНОСТЕЙ
- •3.3. ПРИМЕР АНАЛИТИЧЕСКОГО СПОСОБА ЗАДАНИЯ ПОВЕРХНОСТИ
- •4. ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ ПОВЕРХНОСТЕЙ
- •4.1. ТРЕХГРАННИК ФРЕНЕ
- •4.2. ЕСТЕСТВЕННЫЕ КООРДИНАТЫ ПРОСТРАНСТВЕННОЙ КРИВОЙ
- •5. КРИВЫЕ ЛИНИИ НА СФЕРЕ
- •6. КАСАТЕЛЬНЫЕ И НОРМАЛИ К ПОВЕРХНОСТИ ПРИ ОБРАБОТКЕ ЕЕ НА СТАНКАХ С ЧПУ
- •7.2. КАРКАСНО-КИНЕМАТИЧЕСКИЙ МЕТОД ПРОЕКТИРОВАНИЯ
- •ВЫВОДЫ
- •УПРАЖНЕНИЕ
- •Порядок выполнения
- •ПОВЕРХНОСТИ ВРАЩЕНИЯ И ВИНТОВЫЕ
- •1. ПОВЕРХНОСТИ ВРАЩЕНИЯ
- •3. ПРИМЕРЫ ПОВЕРХНОСТЕЙ ВРАЩЕНИЯ
- •3.1. СФЕРА
- •3.2. ЦИЛИНДР ВРАЩЕНИЯ
- •3.3. КОНУС ВРАЩЕНИЯ
- •3.4. ГИПЕРБОЛОИД ВРАЩЕНИЯ
- •4. ВИНТОВЫЕ ПОВЕРХНОСТИ
- •4.1. ПРЯМОЙ ГЕЛИКОИД
- •4.2. ДРУГИЕ ВИДЫ ВИНТОВЫХ ПОВЕРХНОСТЕЙ
- •ВЫВОДЫ
- •УПРАЖНЕНИЕ
- •Порядок выполнения
- •ЛИНЕЙЧАТЫЕ ПОВЕРХНОСТИ
- •1. СПОСОБ ОБРАЗОВАНИЯ ПОВЕРХНОСТЕЙ ДВИЖЕНИЕМ ПРЯМОЙ ЛИНИИ
- •2.1. КОНИЧЕСКИЕ ПОВЕРХНОСТИ
- •2.2. ЦИЛИНДРИЧЕСКИЕ ПОВЕРХНОСТИ
- •3. ЛИНЕЙЧАТЫЕ ПОВЕРХНОСТИ
- •3.1. ЦИЛИНДРОИД
- •3.2. КОНОИД
- •3.3. ГИПЕРБОЛИЧЕСКИЙ ПАРАБОЛОИД (КОСАЯ ПЛОСКОСТЬ)
- •ВЫВОДЫ
- •УПРАЖНЕНИЕ
- •Порядок выполнения
- •ГЛАВА 13
- •РАЗВЕРТКИ ПОВЕРХНОСТЕЙ
- •1. ПЛОСКОСТЬ, КАСАТЕЛЬНАЯ К ПОВЕРХНОСТИ
- •1.1. ОСНОВНЫЕ ПОНЯТИЯ
- •1.2. ПОСТРОЕНИЕ КАСАТЕЛЬНОЙ ПЛОСКОСТИ
- •2. РАЗВЕРТКИ ПОВЕРХНОСТЕЙ
- •2.1. ПОРЯДОК ПОСТРОЕНИЯ РАЗВЕРТОК В ОБЩЕМ СЛУЧАЕ
- •2.2. ОСНОВНЫЕ СВОЙСТВА РАЗВЕРТЫВАЮЩИХСЯ ПОВЕРХНОСТЕЙ
- •2.3. ПРИМЕРЫ РАЗВЕРТЫВАНИЯ КРИВЫХ ПОВЕРХНОСТЕЙ
- •Прямой круговой цилиндр
- •Наклонный цилиндр
- •Конус
- •2.4. РАЗВЕРТКИ НЕРАЗВЕРТЫВАЮЩИХСЯ ПОВЕРХНОСТЕЙ
- •ВЫВОДЫ
- •УПРАЖНЕНИЕ
- •Задача № 1
- •Порядок выполнения
- •Задача № 2
- •Порядок выполнения
- •Задача № 3
- •Порядок выполнения
- •Создание конуса с вырезом
- •Создание развертки
- •Задача № 4
- •Порядок выполнения
- •АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ
- •1. ОСНОВНЫЕ ПОНЯТИЯ
- •2. СУТЬ СПОСОБА ПОЛУЧЕНИЯ АКСОНОМЕТРИЧЕСКИХ ПРОЕКЦИЙ
- •5. СТАНДАРТНЫЕ ВИДЫ АКСОНОМЕТРИЧЕСКИХ ПРОЕКЦИЙ
- •5.1. ПРЯМОУГОЛЬНАЯ ИЗОМЕТРИЯ
- •5.1.1. ОКРУЖНОСТЬ В ПРЯМОУГОЛЬНОЙ ИЗОМЕТРИИ
- •5.2. ПРЯМОУГОЛЬНАЯ ДИМЕТРИЯ
- •6. КОСОУГОЛЬНЫЕ АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ
- •6.1. ФРОНТАЛЬНАЯ ИЗОМЕТРИЧЕСКАЯ ПРОЕКЦИЯ
- •6.2. ГОРИЗОНТАЛЬНАЯ ИЗОМЕТРИЧЕСКАЯ ПРОЕКЦИЯ
- •6.3. ФРОНТАЛЬНАЯ ДИМЕТРИЧЕСКАЯ ПРОЕКЦИЯ
- •ВЫВОДЫ
- •ГЛАВА 15
- •1. ПАРАМЕТРИЗАЦИЯ МАКРОГЕОМЕТРИИ ПОВЕРХНОСТЕЙ ТЕХНИЧЕСКИХ ИЗДЕЛИЙ
- •1.3. ЗАДАНИЕ РАЗМЕРОВ
- •1.3.1. БАЗИРОВАНИЕ И БАЗЫ
- •1.3.2. КОЛИЧЕСТВО РАЗМЕРОВ ДЛЯ ПОЛНОГО ОПРЕДЕЛЕНИЯ ФОРМЫ ДЕТАЛЕЙ
- •1.3.3. РАЗМЕРЫ ФОРМЫ И РАЗМЕРЫ ПОЛОЖЕНИЯ ПОВЕРХНОСТЕЙ
- •1.3.4. КОНСТРУКТИВНАЯ НЕОПРЕДЕЛЕННОСТЬ БАЗ
- •1.4. НАНЕСЕНИЕ РАЗМЕРОВ
- •1.5. ОСЕВЫЕ И ЦЕНТРОВЫЕ ЛИНИИ
- •2. ПАРАМЕТРИЗАЦИЯ МИКРОГЕОМЕТРИИ ПОВЕРХНОСТЕЙ ТЕХНИЧЕСКИХ ИЗДЕЛИЙ
- •ВЫВОДЫ
- •УПРАЖНЕНИЕ
- •Задача № 1
- •Задача № 2
- •Порядок выполнения
- •ЗАКЛЮЧЕНИЕ
- •БИБЛИОГРАФИЧЕСКИЙ СПИСОК
- •ОГЛАВЛЕНИЕ
Г л а в а 14. Аксонометрические проекции |
323 |
5. СТАНДАРТНЫЕ ВИДЫ АКСОНОМЕТРИЧЕСКИХ ПРОЕКЦИЙ
На практике пользуются аксонометрическими проекциями, которые обеспечивают простоту построений. Для них стандартизованы углы между осями, показатели искажений и т. д.
Согласно ГОСТ 2.317–69 из прямоугольных аксонометрических проекций рекомендуется применять прямоугольные изометрию и диметрию, из косоугольных – фронтальную и горизонтальную изометрические проекции, а также фронтальную диметрическую проекцию.
Наиболее распространенными аксонометрическими проекциями являются прямоугольные.
Приведем краткие сведения об этих проекциях.
5.1. ПРЯМОУГОЛЬНАЯ ИЗОМЕТРИЯ
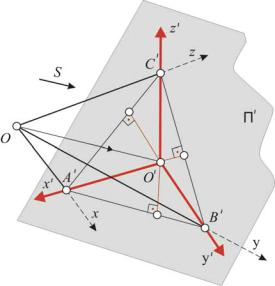
Показатели искажений по трем осям одинаковы: u = v = w. Плоскость аксонометрических проекций наклонена к координатным осям под равными углами и отсекает на всех трех осях равные отрезки ОА′ = ОВ′ = ОС′. В этом случае треугольник следов А′В′С′ равносторонний (рис. 5).
Рис. 5
324 |
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ИНЖЕНЕРНОЙ ГРАФИКИ |
В теории ортогональных аксонометрических проекций доказывается, что аксонометрические оси являются высотами треугольника следов. Из элементарной геометрии известно, что в равностороннем треугольнике высоты попарно пересекаются между собой под углом 120°. Поэтому совпадающие с ними аксонометрические оси в ортогональной изометрии образуют между собой углы в 120°. Обычно ось z принимают вертикальной. Мы уже знаем, что
в прямоугольной аксонометрии u2 + v2 + w2 = 2, а в изометрии u = v = w. Это значит, что 3u2 = 2, откуда
u = |
2 |
≈0,82, |
|
3 |
|
т. е. изометрический масштаб измерения равен 0,82 натурального.
Значения координат любой из точек пространства при построении ее аксонометрической проекции надо умножать на коэффициент 0,82, а соответствующие этим числам отрезки откладывать по направлениям аксонометрических осей.
На практике при построении аксонометрических изображений коэффициент искажения берут равным единице. Изометрические изображения тогда становятся увеличенными в 1,22 раза (1 : 0,82 = 1,22).
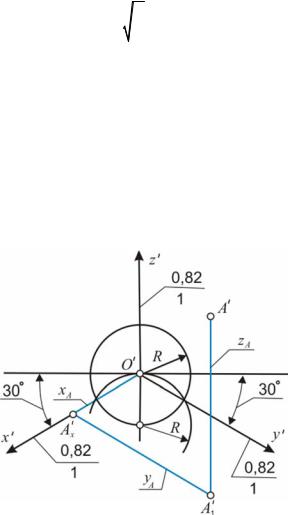
На рис. 6 показано построение изометрической проекции точки А. Построение осей выполнено с помощью окружности произвольного радиуса R.
Рис. 6
Г л а в а 14. Аксонометрические проекции |
325 |
5.1.1. ОКРУЖНОСТЬ В ПРЯМОУГОЛЬНОЙ ИЗОМЕТРИИ
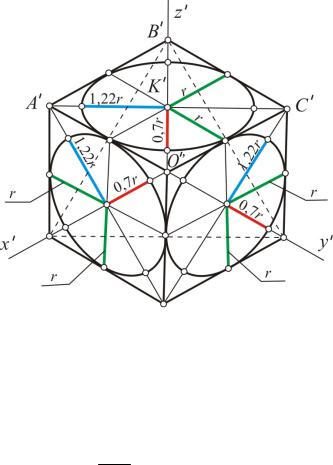
Построим изометрическую проекцию куба (рис. 7). Аксонометрические оси x′, y′, z′ совпадают с направлением ребер куба. Очевидно, грани куба (квадра-
ты) изобразятся ромбами, а окружности – эллипсами. Центры симметрии
Рис. 7
квадратов (окружностей) в изометрии являются центрами симметрии ромбов (эллипсов). Диаметры окружностей, параллельные координатным осям, изображаются сопряженными диаметрами эллипсов (их величина равна диаметру окружности). Из прямоугольного треугольника B′K′A′ , расположенного в верхней грани куба (на рис. 8 он показан отдельно), имеем
BA′′KK′′ = tg 30° = 0,58.
Очевидно, что и отношение полуосей эллипса то же: ba = 0,58 , откуда b = 0,58a.
Здесь большая ось эллипса равна диаметру d окружности, т. е. 2а = d, а малая ось 2b = 0,58 · 2a = 0,58d. Если не учитывать показателей искажения, все
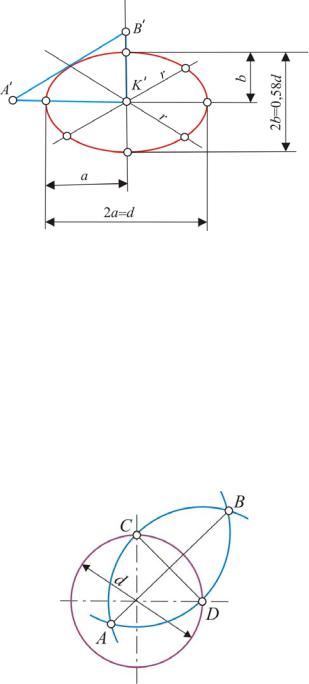
326 |
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ИНЖЕНЕРНОЙ ГРАФИКИ |
d – диаметр окружности r – радиус окружности
Рис. 8
размеры изображения увеличиваются в 1,22 раза. Увеличиваются и оси эллипсов:
2a = 1,22d;
2b = 1,22 · 0,58d = 0,71d.
Таким образом, у эллипса: большая ось равна 1,22d; малая ось равна 0,71d.
На рис. 7 эти увеличенные оси помечены своими половинами – 1,22r и 0,7r.
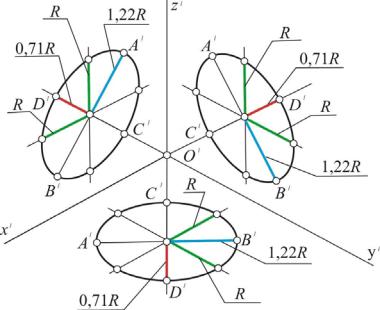
Рис. 9
Г л а в а 14. Аксонометрические проекции |
327 |
Величины осей эллипса можно определить графически (рис. 9). Малая ось эллипса СD равняется хорде, стягивающей одну четвертую часть изображаемой окружности диаметром d.
Концы А и В большой оси находят засечками из центров C и D радиусом
R = CD.
Направление большой оси эллипса в прямоугольной аксонометрии всегда перпендикулярно к той оси, которая отсутствует в плоскости изображаемой окружности: А′В′ z′ в плоскости x′O′y′, А′В′ y′ в плоскости x′O′z′, А′В′ x′ в плоскости y′O′z′ (рис. 10).
Рис. 10
Эллипсы целесообразно строить по следующему плану:
•найти проекцию центра эллипса;
•через найденную точку провести прямую, перпендикулярную соответствующей аксонометрической оси, и на ней отложить по обе стороны от проекции центра по 1,22R, где R – радиус окружности;
•провести прямую, перпендикулярную большой оси, и на ней от проекции центра по обе стороны отложить по 0,7R;
•на прямых, параллельных аксонометрическим осям, отложить отрезки длиной r;
328 |
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ИНЖЕНЕРНОЙ ГРАФИКИ |
• полученные таким образом восемь точек соединить плавной кривой линией.
Изометрические проекции применяют в тех случаях, когда элементы предмета по трем взаимно перпендикулярным направлениям одинаково важны.
5.1.2.ПРИМЕР ПОСТРОЕНИЯ ГЕОМЕТРИЧЕСКОГО ОБЪЕКТА
ВПРЯМОУГОЛЬНОЙ ИЗОМЕТРИИ
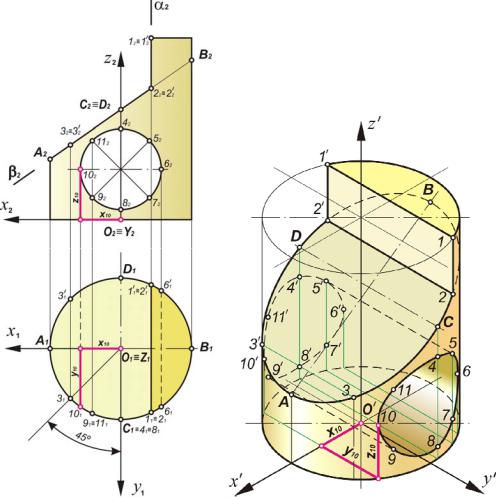
Построить прямоугольную изометрию прямого кругового цилиндра с вырезом и сквозным отверстием цилиндрической формы (рис. 11). Вырез образован плоскостями: профильной α и фронтально проецирующей β . Плоскость
α пересекает верхнее основание цилиндра по линии 1−1′, которая проецируется в натуральную величину на горизонтальной проекции. Фронтально проецирующая прямая, получающаяся от пересечения плоскостей α и β, ограни-
чена на цилиндрической поверхности точками 2 −2′. Следовательно, площадка, образованная сечением цилиндра плоскостью α , представляет прямоугольник 1−1′– 2′−2 .
Плоскость β, наклоненная к оси цилиндра, пересекает его поверхность по
эллипсу, большой осью которого является отрезок АВ, а величина малой оси CD равна диаметру цилиндра. В нашем случае эллипс будет неполным, так как ограничен линией 2 −2′. Горизонтальная проекция эллипса совпадает с горизонтальной проекцией цилиндрической поверхности – окружностью.
Для построения изометрии цилиндра вначале соотносим его на ортогональном чертеже с прямоугольной системой декартовых координат, обозначив оси буквами x , y , z . Начало координат удобно поместить в центре ок-
ружности нижнего основания. Теперь на свободном месте чертежа проводим направления аксонометрических осей x′ , y′ , z′ для прямоугольной изо-
метрии.
Определив величины большой и малой осей эллипса (графический способ показан на рис. 9), построим нижнее и верхнее основания цилиндра, а затем весь цилиндр в тонких линиях с изображением вертикальной площадки в виде прямоугольника 1−1′– 2′−2 .
При построении эллипса, получаемого сечением цилиндра плоскостью β,
отмеченных характерных точек |
′ |
A − B, C − D недостаточно, поэтому |
2 −2 , |
отметим хотя бы еще пару точек 3 −3′. Для удобства построения их в аксонометрии пусть они находятся на равном расстоянии от осей x , y , что видно на
Г л а в а 14. Аксонометрические проекции |
329 |
Рис. 11
горизонтальной проекции цилиндра, где показан угол 45°. Построение аксонометрической проекции любой точки объекта делается посредством измерения ее координат на ортогональном чертеже и нанесения их значений на соответствующие аксонометрические оси. Это показано для одной из отмеченных на контуре цилиндрического выреза точки 10. Соединив построенные таким образом точки в аксонометрии плавными кривыми линиями, получим изображение эллипса с его осями: большой – АВ и малой – CD и цилиндрического отверстия.
