рых является ребро возврата. Если пересечь торсовую поверхность плоскостью, перпендикулярной к образующей в точке ее касания, то в сечении получается кривая линия вида MKN. Точка K этой линии является особой точкой – точкой возврата. Таким образом, все точки ребра возврата являются особыми точками, т. е. точками возврата. Поэтому и направляющая кривая линия называется ребром возврата. Это ребро возврата служит определителем торсовой

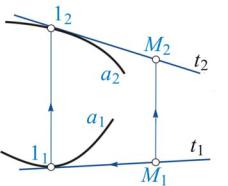
поверхности. На эпюре торсовая поверхность Ф задается проекциями a1 и a2 ребра возврата (рис. 8).

Рис. 8

Для построения точки М Ф по одной заданной проекции, например M1, проводим горизонтальную проекцию образующей – прямую t1, касательную к

a1 (M1 t1).

Отмечаем точку касания 11, находим ее фронтальную проекцию 12 a2 и проводим фронтальную проекцию t2 образующей, касающуюся a2 в точке 12.

Фронтальная проекция M2 точки M принадлежит t2.

Если ребро возврата преобразовать в плоскуюкривую, то поверхность торса выродится в отсек плоскости, если ребро возврата преобразовать в точку, то получится коническая поверхность с вершиной в этой точке (если точка собственная) или цилиндрическая поверхность (если точка несобственная).

2.1. КОНИЧЕСКИЕ ПОВЕРХНОСТИ

Коническая поверхность образуется перемещением прямой, проходящей через неподвижную точку S (вершину) и пересекающей некоторую линию m

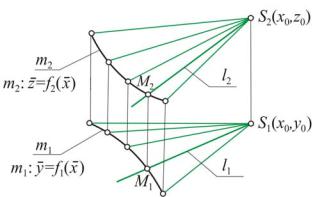
(направляющую). На эпюре Монжа поверхность задается проекциями S(S1, S2) и направляющей m(m1, m2) (рис. 9).

Рис. 9

Пусть некоторая прямая l (l1, l2) проходит через точку М направляющей и вершину S. Эта линия является образующей конической поверхности. Изображение поверхности проекциями вершины и направляющей не наглядно, поэтому его пополняют проекциями l1, l2, …, ln достаточно плотного каркаса образующих.

Уравнение прямой, проходящей через вершину S и точку М с координатами М1( x, y ) и М2( x, z ), имеет вид

Так как точка М перемещается по линии m, то к уравнению прямой надо добавить еще уравнения проекций m1 и m2:

m1 : y = f1 (x ); m2 : z = f2 (x ).

Уравнение конической поверхности выводится из совместного решения уравнений образующей l и направляющей m. Исключая x, y, z , получаем

уравнение конической поверхности F (x, y, z) = 0.

2.2. ЦИЛИНДРИЧЕСКИЕ ПОВЕРХНОСТИ

Цилиндрические поверхности – это поверхности, образованные перемещением прямой образующей l, при котором она, оставаясь параллельной одной и той же прямой s, пересекает некоторую линию а (направляющую).

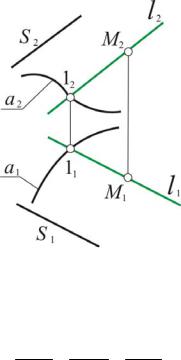
На эпюре Монжа достаточно задать проекции а1, а2 направляющей а и направление образующей s (рис. 10). Полноту задания цилиндрической поверхности проверяем построением проекции М1 точки М Ф(а, s). Через точку М1 проводим l1 // s1. Отмечаем точку 11 пересечения l1 и а1. По линии связи на а2 находим точку 12, через которую проводим l2 // s2. По линии связи на l2 отмечаем искомую точку М2.

Рис. 10

Уравнение цилиндрической поверхности выводится совместным решением уравнений образующей и направляющей:

x −mx1 = y −n y1 = z −pz1 ,

a1: y1 = f1(x1),

a2: z2 = f2(x2).

Исключая x1, y1, z1, получаем уравнение цилиндрической поверхности

Ф (x, y, z) = 0.

3.ЛИНЕЙЧАТЫЕ ПОВЕРХНОСТИ

СДВУМЯ НАПРАВЛЯЮЩИМИ

ИПЛОСКОСТЬЮ ПАРАЛЛЕЛИЗМА (ПОВЕРХНОСТИ КАТАЛАНА)

Линейчатая поверхность, образованная движением прямой линии (образующей) по двум направляющим линиям параллельно какой-либо плоскости, называется поверхностью с плоскостью параллелизма.

В зависимости от формы направляющих получаются разные виды поверхностей: цилиндроиды, коноиды и гиперболические параболоиды. Эти поверхности впервые подробно исследовал бельгийский ученый Е. Каталан, поэтому их еще называют поверхностями Каталана. Рассмотрим эти поверхности.

3.1. ЦИЛИНДРОИД

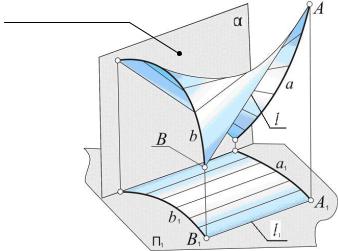
Цилиндроид – неразвертывающаяся линейчатая поверхность, имеющая плоскость параллелизма и две криволинейные направляющие (рис. 11).

Плоскость

параллелизма

Рис. 11

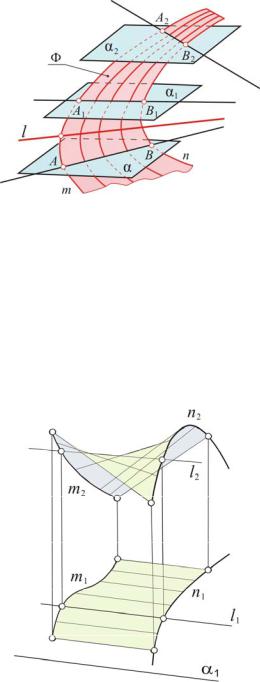
Пусть дана некоторая плоскость α и две какие-нибудь кривые m и n (рис. 12). Будем перемещать прямую l так, чтобы она пересекала их, оставаясь все время параллельной этой плоскости.

Рис. 12

Плоскость α называется плоскостью параллелизма, а поверхность Ф, образованная движением прямой l, называется цилиндроидом. Семейство параллельных плоскостей, проходящих через отдельные положения образующей, пересекаются между собой по несобственной прямой, которая является третьей направляющей, удаленной в бесконечность.

Таким образом, каждая образующая пересекает плоскость α в несобственной точке, находящейся на этой третьей направляющей. Определитель поверхности: Ф [m, n, α], где m, n – направляющие; α – плоскость параллелизма.

На рис. 13 показан цилиндроид в прямоугольных проекциях (на эпюре).

Рис. 13

Аналитическое выражение цилиндроида. Пусть даны уравнения проек-

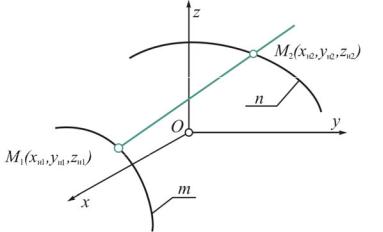
ций двух направляющих линий m и n цилиндроида (рис. 14): m: y1 = f1(xн1),

z1 = ϕ1 (xн1),

n: y2 = f2(xн2),

z2 = ϕ2 (xн2)

иплоскости параллелизма в нормальном виде:

xcos α + y cos β + z cos γ – p = 0,

где cos α, cos β, cos γ – направляющие косинусы нормали к плоскости; p – расстояние от начала координат до плоскости.

Рис. 14

Возьмем точки М1 и М2 на направляющих m и n, тогда: yн1 = f1(xн1); zн1 = ϕ1 (xн1);

yн2 = f2(xн2); zн2 = ϕ2 (xн2); M1 [xн1, f1(xн1), ϕ1 (xн1)]; M2 [xн2, f2(xн2), ϕ2 (xн2)].