
- •ПРЕДИСЛОВИЕ
- •ВВЕДЕНИЕ
- •ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ИНЖЕНЕРНОЙ ГРАФИКИ
- •Элберт Хаббард
- •ПРИНЯТЫЕ ОБОЗНАЧЕНИЯ
- •ГЛАВА 1
- •ОСНОВНЫЕ ПОНЯТИЯ В ТЕОРИИ ИЗОБРАЖЕНИЯ ГЕОМЕТРИЧЕСКИХ ОБЪЕКТОВ
- •1. ЧТО ТАКОЕ НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ?
- •2. ГЕОМЕТРИЧЕСКОЕ МОДЕЛИРОВАНИЕ – ИНСТРУМЕНТ ПОЗНАНИЯ ДЕЙСТВИТЕЛЬНОСТИ
- •4. ПРОЕКЦИОННОЕ ОТОБРАЖЕНИЕ – АНАЛОГ ПОНЯТИЯ ФУНКЦИИ
- •Свойства центрального проецирования
- •Свойства параллельного проецирования
- •5. МЕТОД ДВУХ ИЗОБРАЖЕНИЙ
- •6. МОДЕЛЬ ТОЧКИ В ОРТОГОНАЛЬНЫХ ПРОЕКЦИЯХ
- •ВЫВОДЫ
- •ПРЯМАЯ ЛИНИЯ И ПЛОСКОСТЬ
- •1. ПОЛОЖЕНИЕ ПРЯМОЙ В ПРОСТРАНСТВЕ
- •3. ВЗАИМНОЕ ПОЛОЖЕНИЕ ДВУХ ПРЯМЫХ
- •4. ПОЛОЖЕНИЕ ПЛОСКОСТИ В ПРОСТРАНСТВЕ
- •5. РАСПОЛОЖЕНИЕ ПЛОСКОСТИ ОТНОСИТЕЛЬНО ОСНОВНЫХ ПЛОСКОСТЕЙ ПРОЕКЦИЙ
- •Проецирующая плоскость
- •Плоскость уровня
- •ВЫВОДЫ
- •УПРАЖНЕНИЕ
- •Задача № 1
- •Порядок выполнения
- •Задача № 2
- •Порядок выполнения
- •Задача № 3
- •Порядок выполнения
- •Задача № 4
- •Порядок выполнения
- •Задача № 5
- •Порядок выполнения
- •ГЛАВА 3
- •СПОСОБЫ ПРЕОБРАЗОВАНИЯ ПРОЕКЦИЙ
- •1. ПРИНАДЛЕЖНОСТЬ ПРЯМОЙ ЛИНИИ ПЛОСКОСТИ
- •1.1. ПРЯМАЯ ОБЩЕГО ПОЛОЖЕНИЯ В ПЛОСКОСТИ
- •1.2. ГЛАВНЫЕ ЛИНИИ ПЛОСКОСТИ
- •Линии уровня
- •Линии наибольшего наклона плоскости
- •2. СПОСОБЫ ПРЕОБРАЗОВАНИЯ ПРОЕКЦИЙ
- •2.1. ПЛОСКОПАРАЛЛЕЛЬНОЕ ПЕРЕМЕЩЕНИЕ
- •2.2. ВРАЩЕНИЕ ВОКРУГ ОСЕЙ, ПЕРПЕНДИКУЛЯРНЫХ ПЛОСКОСТЯМ ПРОЕКЦИЙ
- •2.3. ВРАЩЕНИЕ ВОКРУГ ОСЕЙ, ПАРАЛЛЕЛЬНЫХ ПЛОСКОСТЯМ ПРОЕКЦИЙ
- •2.4. ВРАЩЕНИЕ ВОКРУГ ОСЕЙ, ЛЕЖАЩИХ В ПЛОСКОСТЯХ ПРОЕКЦИЙ (СОВМЕЩЕНИЕ С ПЛОСКОСТЯМИ ПРОЕКЦИЙ)
- •2.5. ЗАМЕНА ПЛОСКОСТЕЙ ПРОЕКЦИЙ
- •ВЫВОДЫ
- •УПРАЖНЕНИЕ
- •ГЛАВА 4
- •ОБОБЩЕННЫЕ ПОЗИЦИОННЫЕ ЗАДАЧИ
- •1.1. ПРЯМАЯ ЛИНИЯ, ПАРАЛЛЕЛЬНАЯ ПЛОСКОСТИ
- •1.2. ПРЯМАЯ ЛИНИЯ, ПЕРЕСЕКАЮЩАЯ ПЛОСКОСТЬ (ОБЩИЙ СЛУЧАЙ)
- •1.3. ПРЯМАЯ ЛИНИЯ, ПЕРПЕНДИКУЛЯРНАЯ ПЛОСКОСТИ
- •2. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПЛОСКОСТЕЙ
- •2.1. ПЛОСКОСТИ ПАРАЛЛЕЛЬНЫЕ
- •2.2. ПЛОСКОСТИ ПЕРЕСЕКАЮЩИЕСЯ (ОБЩИЙ СЛУЧАЙ)
- •2.3. ПЛОСКОСТИ ВЗАИМНО ПЕРПЕНДИКУЛЯРНЫЕ
- •3. ВЗАИМНО ПЕРПЕНДИКУЛЯРНЫЕ ПРЯМЫЕ
- •4. ОБОБЩЕННЫЕ ПОЗИЦИОННЫЕ ЗАДАЧИ
- •4.1. ПЕРЕСЕЧЕНИЕ КРИВОЙ ЛИНИИ С ПОВЕРХНОСТЬЮ
- •4.2. ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ
- •4.3. ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА
- •ВЫВОДЫ
- •УПРАЖНЕНИЕ
- •Задача № 1
- •Порядок выполнения
- •Задача № 2
- •Порядок выполнения
- •Задача № 3
- •Порядок выполнения
- •Задача № 4
- •Порядок выполнения
- •Задача № 5
- •Порядок выполнения
- •ГЛАВА 5
- •1. ОБ АНАЛОГИИ МЕЖДУ ПОНЯТИЯМИ «ФУНКЦИЯ» И «ОТОБРАЖЕНИЕ»
- •2. ПЕРСПЕКТИВНАЯ КОЛЛИНЕАЦИЯ
- •Теорема Дезарга
- •Гомология
- •3. ПЕРСПЕКТИВНО-АФФИННОЕ (РОДСТВЕННОЕ) СООТВЕТСТВИЕ
- •4. СРАВНЕНИЕ ДВУХ ГОМОЛОГИЙ
- •ВЫВОДЫ
- •УПРАЖНЕНИЕ
- •Порядок выполнения
- •ГЛАВА 6
- •ПРОЕКЦИОННЫЕ МОДЕЛИ ТРЕХМЕРНЫХ ОБЪЕКТОВ
- •1. ВНЕШНЯЯ ФОРМА ПРЕДМЕТОВ И НЕОБХОДИМОСТЬ ВЫЯВЛЕНИЯ ИХ ВНУТРЕННИХ КОНТУРОВ
- •2. СИСТЕМЫ РАСПОЛОЖЕНИЯ ИЗОБРАЖЕНИЙ
- •3. ВИДЫ
- •3.1. ОСНОВНЫЕ ВИДЫ
- •3.2. ДОПОЛНИТЕЛЬНЫЕ ВИДЫ
- •3.3. МЕСТНЫЕ ВИДЫ
- •4. РАЗРЕЗЫ
- •4.1. ВИДЫ РАЗРЕЗОВ
- •4.2. ОБОЗНАЧЕНИЕ РАЗРЕЗОВ
- •5. СЕЧЕНИЯ
- •ВЫВОДЫ
- •УПРАЖНЕНИЕ
- •Задача № 1
- •Порядок выполнения
- •Задача № 2
- •Порядок выполнения
- •КРИВЫЕ ЛИНИИ
- •1. СПОСОБЫ ОБРАЗОВАНИЯ КРИВЫХ ЛИНИЙ
- •2. КЛАССИФИКАЦИЯ КРИВЫХ ЛИНИЙ
- •3. СПОСОБЫ ЗАДАНИЯ КРИВЫХ ЛИНИЙ
- •4. КАСАТЕЛЬНАЯ И НОРМАЛЬ К КРИВОЙ ЛИНИИ
- •5. УРАВНЕНИЯ КАСАТЕЛЬНОЙ И НОРМАЛИ
- •6. ВЕКТОР-ФУНКЦИЯ
- •7. КРИВИЗНА КРИВОЙ
- •8. КРУГ КРИВИЗНЫ
- •9. ЭВОЛЮТА И ЭВОЛЬВЕНТА
- •10. КРИВИЗНА ОКРУЖНОСТИ
- •11. КРИВЫЕ ЛИНИИ ВТОРОГО ПОРЯДКА
- •11.1. ЭЛЛИПС
- •11.2. ПАРАБОЛА
- •11.3. ГИПЕРБОЛА
- •12. КОНИЧЕСКИЕ СЕЧЕНИЯ
- •13. ПРОЕКЦИИ КРИВЫХ ЛИНИЙ
- •14. ЭЛЛИПС – ФИГУРА, РОДСТВЕННАЯ ОКРУЖНОСТИ
- •15. ОКРУЖНОСТЬ В ПЛОСКОСТИ ОБЩЕГО ПОЛОЖЕНИЯ
- •15.2. ОПРЕДЕЛЕНИЕ ВЕЛИЧИНЫ МАЛОЙ ОСИ ЭЛЛИПСА МЕТОДОМ ЗАМЕНЫ ПЛОСКОСТЕЙ ПРОЕКЦИЙ
- •15.3. ОПРЕДЕЛЕНИЕ ВЕЛИЧИНЫ МАЛОЙ ОСИ ЭЛЛИПСА С ПРИМЕНЕНИЕМ ЛИНИИ НАИБОЛЬШЕГО НАКЛОНА ПЛОСКОСТИ
- •ВЫВОДЫ
- •УПРАЖНЕНИЕ
- •Порядок выполнения
- •ГЛАВА 8
- •КРИВЫЕ ЛИНИИ, ИМЕЮЩИЕ ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ.
- •ОБВОДЫ ПРИ ПРОЕКТИРОВАНИИ ПОВЕРХНОСТЕЙ
- •1. НЕКОТОРЫЕ ПЛОСКИЕ КРИВЫЕ, ИМЕЮЩИЕ ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ
- •1.1. ЦИКЛИЧЕСКИЕ КРИВЫЕ
- •Циклоида
- •Эпициклоиды
- •Гипоциклоиды
- •1.2. СПИРАЛИ
- •1.3. ПОДЕРЫ
- •2.ПЛОСКИЕ СОСТАВНЫЕ КРИВЫЕ ЛИНИИ (ОБВОДЫ) ПРИ ПРОЕКТИРОВАНИИ ПОВЕРХНОСТЕЙ
- •2.1. АППРОКСИМАЦИЯ ТОЧЕЧНЫХ МАССИВОВ
- •2.3. ХАРАКТЕРНЫЕ ТОЧКИ КРИВЫХ
- •2.4. ПОРЯДОК ГЛАДКОСТИ ОБВОДОВ
- •2.5. ОСНОВНЫЕ СПОСОБЫ ПОСТРОЕНИЯ ОБВОДОВ
- •2.5.1. ИНТЕРПОЛЯЦИЯ ДУГАМИ ОКРУЖНОСТЕЙ
- •2.5.2. ИНТЕРПОЛЯЦИЯ КРИВЫМИ ВТОРОГО ПОРЯДКА
- •2.5.3. ИНТЕРПОЛЯЦИЯ ОБВОДОВ СПЛАЙН-ФУНКЦИЯМИ
- •ВЫВОДЫ
- •ГЛАВА 9
- •МНОГОГРАННЫЕ ПОВЕРХНОСТИ И МНОГОГРАННИКИ.
- •СИСТЕМАТИЗАЦИЯ ПОВЕРХНОСТЕЙ
- •1. МНОГОГРАННЫЕ ПОВЕРХНОСТИ
- •2. НЕКОТОРЫЕ ВИДЫ МНОГОГРАННИКОВ
- •3. ПЕРЕСЕЧЕНИЕ МНОГОГРАННИКА ПЛОСКОСТЬЮ
- •5. ВЗАИМНОЕ ПЕРЕСЕЧЕНИЕ МНОГОГРАННИКОВ
- •6. РАЗВЕРТКИ МНОГОГРАННИКОВ
- •6.1. СПОСОБ НОРМАЛЬНОГО СЕЧЕНИЯ
- •6.2. СПОСОБ РАСКАТКИ
- •6.3. СПОСОБ ТРЕУГОЛЬНИКОВ (ТРИАНГУЛЯЦИИ)
- •7. СИСТЕМАТИЗАЦИЯ ПОВЕРХНОСТЕЙ
- •ВЫВОДЫ
- •УПРАЖНЕНИЕ
- •Порядок выполнения
- •СЛОЖНЫЕ ПОВЕРХНОСТИ
- •1. ОПРЕДЕЛЕНИЕ ПОВЕРХНОСТИ
- •2. СПОСОБЫ ОБРАЗОВАНИЯ ПОВЕРХНОСТЕЙ
- •2.1. ОБРАЗОВАНИЕ ПОВЕРХНОСТЕЙ ПРИ ПОМОЩИ ДВИЖУЩЕЙСЯ ЛИНИИ
- •2.2. ОБРАЗОВАНИЕ ПОВЕРХНОСТЕЙ ПРИ ПОМОЩИ ДВИЖУЩЕЙСЯ ПОВЕРХНОСТИ
- •3. СПОСОБЫ ЗАДАНИЯ ПОВЕРХНОСТЕЙ
- •3.1. ГРАФИЧЕСКИЙ СПОСОБ ЗАДАНИЯ КИНЕМАТИЧЕСКИХ ПОВЕРХНОСТЕЙ
- •3.2. АНАЛИТИЧЕСКИЙ СПОСОБ ЗАДАНИЯ ПОВЕРХНОСТЕЙ
- •3.3. ПРИМЕР АНАЛИТИЧЕСКОГО СПОСОБА ЗАДАНИЯ ПОВЕРХНОСТИ
- •4. ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ ПОВЕРХНОСТЕЙ
- •4.1. ТРЕХГРАННИК ФРЕНЕ
- •4.2. ЕСТЕСТВЕННЫЕ КООРДИНАТЫ ПРОСТРАНСТВЕННОЙ КРИВОЙ
- •5. КРИВЫЕ ЛИНИИ НА СФЕРЕ
- •6. КАСАТЕЛЬНЫЕ И НОРМАЛИ К ПОВЕРХНОСТИ ПРИ ОБРАБОТКЕ ЕЕ НА СТАНКАХ С ЧПУ
- •7.2. КАРКАСНО-КИНЕМАТИЧЕСКИЙ МЕТОД ПРОЕКТИРОВАНИЯ
- •ВЫВОДЫ
- •УПРАЖНЕНИЕ
- •Порядок выполнения
- •ПОВЕРХНОСТИ ВРАЩЕНИЯ И ВИНТОВЫЕ
- •1. ПОВЕРХНОСТИ ВРАЩЕНИЯ
- •3. ПРИМЕРЫ ПОВЕРХНОСТЕЙ ВРАЩЕНИЯ
- •3.1. СФЕРА
- •3.2. ЦИЛИНДР ВРАЩЕНИЯ
- •3.3. КОНУС ВРАЩЕНИЯ
- •3.4. ГИПЕРБОЛОИД ВРАЩЕНИЯ
- •4. ВИНТОВЫЕ ПОВЕРХНОСТИ
- •4.1. ПРЯМОЙ ГЕЛИКОИД
- •4.2. ДРУГИЕ ВИДЫ ВИНТОВЫХ ПОВЕРХНОСТЕЙ
- •ВЫВОДЫ
- •УПРАЖНЕНИЕ
- •Порядок выполнения
- •ЛИНЕЙЧАТЫЕ ПОВЕРХНОСТИ
- •1. СПОСОБ ОБРАЗОВАНИЯ ПОВЕРХНОСТЕЙ ДВИЖЕНИЕМ ПРЯМОЙ ЛИНИИ
- •2.1. КОНИЧЕСКИЕ ПОВЕРХНОСТИ
- •2.2. ЦИЛИНДРИЧЕСКИЕ ПОВЕРХНОСТИ
- •3. ЛИНЕЙЧАТЫЕ ПОВЕРХНОСТИ
- •3.1. ЦИЛИНДРОИД
- •3.2. КОНОИД
- •3.3. ГИПЕРБОЛИЧЕСКИЙ ПАРАБОЛОИД (КОСАЯ ПЛОСКОСТЬ)
- •ВЫВОДЫ
- •УПРАЖНЕНИЕ
- •Порядок выполнения
- •ГЛАВА 13
- •РАЗВЕРТКИ ПОВЕРХНОСТЕЙ
- •1. ПЛОСКОСТЬ, КАСАТЕЛЬНАЯ К ПОВЕРХНОСТИ
- •1.1. ОСНОВНЫЕ ПОНЯТИЯ
- •1.2. ПОСТРОЕНИЕ КАСАТЕЛЬНОЙ ПЛОСКОСТИ
- •2. РАЗВЕРТКИ ПОВЕРХНОСТЕЙ
- •2.1. ПОРЯДОК ПОСТРОЕНИЯ РАЗВЕРТОК В ОБЩЕМ СЛУЧАЕ
- •2.2. ОСНОВНЫЕ СВОЙСТВА РАЗВЕРТЫВАЮЩИХСЯ ПОВЕРХНОСТЕЙ
- •2.3. ПРИМЕРЫ РАЗВЕРТЫВАНИЯ КРИВЫХ ПОВЕРХНОСТЕЙ
- •Прямой круговой цилиндр
- •Наклонный цилиндр
- •Конус
- •2.4. РАЗВЕРТКИ НЕРАЗВЕРТЫВАЮЩИХСЯ ПОВЕРХНОСТЕЙ
- •ВЫВОДЫ
- •УПРАЖНЕНИЕ
- •Задача № 1
- •Порядок выполнения
- •Задача № 2
- •Порядок выполнения
- •Задача № 3
- •Порядок выполнения
- •Создание конуса с вырезом
- •Создание развертки
- •Задача № 4
- •Порядок выполнения
- •АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ
- •1. ОСНОВНЫЕ ПОНЯТИЯ
- •2. СУТЬ СПОСОБА ПОЛУЧЕНИЯ АКСОНОМЕТРИЧЕСКИХ ПРОЕКЦИЙ
- •5. СТАНДАРТНЫЕ ВИДЫ АКСОНОМЕТРИЧЕСКИХ ПРОЕКЦИЙ
- •5.1. ПРЯМОУГОЛЬНАЯ ИЗОМЕТРИЯ
- •5.1.1. ОКРУЖНОСТЬ В ПРЯМОУГОЛЬНОЙ ИЗОМЕТРИИ
- •5.2. ПРЯМОУГОЛЬНАЯ ДИМЕТРИЯ
- •6. КОСОУГОЛЬНЫЕ АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ
- •6.1. ФРОНТАЛЬНАЯ ИЗОМЕТРИЧЕСКАЯ ПРОЕКЦИЯ
- •6.2. ГОРИЗОНТАЛЬНАЯ ИЗОМЕТРИЧЕСКАЯ ПРОЕКЦИЯ
- •6.3. ФРОНТАЛЬНАЯ ДИМЕТРИЧЕСКАЯ ПРОЕКЦИЯ
- •ВЫВОДЫ
- •ГЛАВА 15
- •1. ПАРАМЕТРИЗАЦИЯ МАКРОГЕОМЕТРИИ ПОВЕРХНОСТЕЙ ТЕХНИЧЕСКИХ ИЗДЕЛИЙ
- •1.3. ЗАДАНИЕ РАЗМЕРОВ
- •1.3.1. БАЗИРОВАНИЕ И БАЗЫ
- •1.3.2. КОЛИЧЕСТВО РАЗМЕРОВ ДЛЯ ПОЛНОГО ОПРЕДЕЛЕНИЯ ФОРМЫ ДЕТАЛЕЙ
- •1.3.3. РАЗМЕРЫ ФОРМЫ И РАЗМЕРЫ ПОЛОЖЕНИЯ ПОВЕРХНОСТЕЙ
- •1.3.4. КОНСТРУКТИВНАЯ НЕОПРЕДЕЛЕННОСТЬ БАЗ
- •1.4. НАНЕСЕНИЕ РАЗМЕРОВ
- •1.5. ОСЕВЫЕ И ЦЕНТРОВЫЕ ЛИНИИ
- •2. ПАРАМЕТРИЗАЦИЯ МИКРОГЕОМЕТРИИ ПОВЕРХНОСТЕЙ ТЕХНИЧЕСКИХ ИЗДЕЛИЙ
- •ВЫВОДЫ
- •УПРАЖНЕНИЕ
- •Задача № 1
- •Задача № 2
- •Порядок выполнения
- •ЗАКЛЮЧЕНИЕ
- •БИБЛИОГРАФИЧЕСКИЙ СПИСОК
- •ОГЛАВЛЕНИЕ
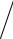
Г л а в а 10. Сложные поверхности |
233 |
6. КАСАТЕЛЬНЫЕ И НОРМАЛИ К ПОВЕРХНОСТИ ПРИ ОБРАБОТКЕ ЕЕ НА СТАНКАХ С ЧПУ
При работе станков с числовым программным управлением (ЧПУ) бывает необходимо вычислять смещения фрезы в трехмерном пространстве [10]. Для этого нужно найти нормаль к тому участку поверхности, который подлежит обработке. Поскольку при обработке поверхности r = r(u, v) фреза следует параметрическим кривым u = const и v = const, в некоторых приложениях большое значение имеют и касательные к этим кривым. Касательный вектор к параметрической кривой r = r(u, v0), где v0 – константа, кратен вектору ∂r/∂u . Подобным же образом касательный вектор к кривой r = r(u0, v) кратен вектору ∂r/∂v . Плоскость, касательная к этим кривым в точке их пересечения r = r(u0, v0), содержит оба указанных выше касательных вектора. Следовательно, нормаль к рассматриваемой поверхности в данной точке кратна векторному произведению этих векторов (рис. 10). Единичный нормальный вектор n определяется по формуле
∂r |
|
∂r |
|
|
∂r |
|
∂r |
|
||
|
|
|
|
|||||||
n = ± |
|
× |
|
|
|
|
× |
|
, |
|
∂u |
∂u |
∂v |
||||||||
|
|
∂v |
|
|
|
|
||||
где производные вычисляются в точке u = u0, v = v0. Ориентация вектора n выбирается в соответствии с рассматриваемым случаем.
Исключительные точки, в которых частные производные не существуют или в которых (∂r/∂u)×(∂r/∂v) = 0 , соответствуют либо особым точкам пара-
метризации, либо гребням или заострениям поверхности.
Предположим, что мы фрезеруем поверхность r = r(u, v) вдоль кривой u = u0 фрезой, имеющей сферический конец радиусом R (рис. 11). Тогда путь верхушки фрезы описывается соотношением
r = r(u0, v) + R(n – u),
где n – единичная нормаль в точке u = u0, а u – единичный вектор оси фрезы; r(u0, v) – точка касания, R(n – u) – смещение фрезы.

234 |
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ИНЖЕНЕРНОЙ ГРАФИКИ |
Рис. 10
Рис. 11
Ориентацию нормали к поверхности следует выбирать таким образом, чтобы вектор n был направлен наружу от обрабатываемой детали.
Г л а в а 10. Сложные поверхности |
235 |
7.ОБВОДЫ ПОВЕРХНОСТЕЙ
ИМЕТОДЫ ИХ ПРОЕКТИРОВАНИЯ
Если посмотреть на такие поверхности, как сфера, эллипсоид вращения, цилиндр или другие поверхности, определяемые уравнениями, то не возникает необходимости употреблять термин «обвод», так как мы имеем дело с цельной поверхностью. По определению профессора В.А. Осипова [17], обводом поверхности называется двумерный комплексный геометрический объект (КГО), составленный из определенных, отвечающих наперед заданным условиям кусков двумерных элементарных геометрических объектов (ЭГО), состыкованных между собой согласно заданным условиям. Куски двумерных ЭГО стыкуются между собой по одномерным ЭГО-линиям плоским или пространственным, вдоль которых необходимо выполнить ряд наперед заданных условий стыковки: порядок гладкости, порядок фиксации и другие дифференциально-геомет- рические характеристики.
Обводы поверхностей формируются двумя методами: каркасно-кусочным (лоскутным), известным под названием метод Кунса, и каркасно-кинематиче- ским. Методы реализуются средствами интерполяции и аппроксимации и отличаются методологией формирования математических моделей объектов.
7.1.КАРКАСНО-КУСОЧНЫЙ МЕТОД ПРОЕКТИРОВАНИЯ
Споявлением ЭВМ процесс проектирования кривых линий и поверхностей стал осуществляться быстрее и с более высокой степенью пространственной целостности, чем при использовании графических методов. Прежде для представления поверхности нужно было построить некоторое множество продольных гладких кривых, проводя их через точки, определяемые предварительно построенным набором поперечных сечений (плазовый метод). Во многих новых методах поперечные и продольные кривые играют одну и ту же роль, разбивая поверхность на некоторую совокупность криволинейных четырехугольных порций. Каждую из этих порций поверхности можно однозначно описать с помощью математической формулы. В 1967 г. Кунс предложил общую теорию построения порций поверхности. Он показал, как соединить четыре произвольные граничные кривые гладкой порцией поверхности и обеспечить непрерывность градиентов и кривизны между ее отдельными порциями.
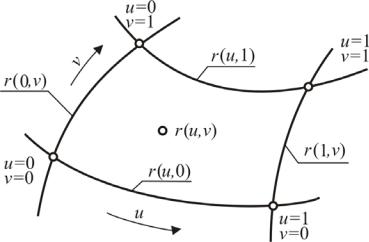
На рис. 12 показана параметрически заданная порция поверхности, взятая из уже построенной каким-либо образом сетки кривых (см. рис. 6). Сетка кривых делит поверхность на совокупность топологически прямоугольных пор-
236 |
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ИНЖЕНЕРНОЙ ГРАФИКИ |
ций, каждая из которых ограничена парой u-кривых и парой v-кривых. Задача определения порции поверхности сводится к нахождению функции r(u, v) c подходящим типом «хорошего поведения», которая при u = 0, u = 1, v = 0 или v = 1 представляет нужную граничную кривую.
Рис. 12
Новые методы в отличие от старых, которые позволяли определять лишь систему линий, лежащих на проектируемой поверхности, но не саму поверхность, явились большим шагом вперед в области проектирования сложных поверхностей.
Большим достижением в области математики было также введение Безье (1971) системы UNISURF, полностью автоматизированной. С ее помощью оператор, не имеющий специальной математической подготовки, может легко проектировать отдельные участки кривых или поверхностей, пользуясь для этого только элементарными геометрическими понятиями. Эта система была первой практической системой проектирования поверхностей, когда проектировщик определяет незамкнутую ломаную, образованную прямолинейными отрезками, изображение которой выводится на дисплей. Система аппроксимирует эту ломаную гладкой кривой. Внося различные модификации в исходную ломаную, проектировщик может изменять аппроксимирующую кривую до тех пор, пока она не будет удовлетворять желаемым критериям. Подобным же образом проектируются и поверхности, но для этого предварительно строится незамкнутая полиэдральная поверхность. Современные компьютерные технологии в полной мере используют эти достижения.
