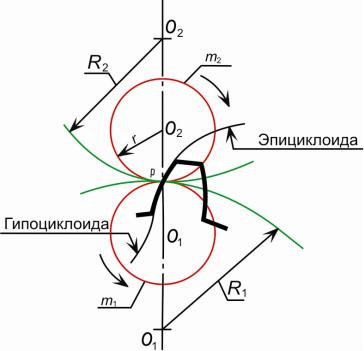
На рис. 11 показан пример применения эпициклоиды и гипоциклоиды при профилировании зубьев зубчатых колес. Головка зуба очерчена по дуге эпи-

циклоиды, а ножка – по дуге гипоциклоиды.

Рис. 11

1.2. СПИРАЛИ

Спирали (от лат. spira – изгиб, виток) – плоские кривые линии, бесчисленное множество раз обходящие некоторую точку, с каждым обходом приближаясь или удаляясь от нее. В технике широко применяют спираль Архимеда. Она образуется точкой, равномерно движущейся по прямой, которая, в свою очередь, равномерно вращается вокруг неподвижной точки. Построение по заданному шагу а: окружность и ее радиус, равный шагу, делят на одинаковое число равных частей и проводят лучи, как показано на рис. 12.

На первом луче откладывают отрезок, равный а/n, на втором 2а/n и т. д. Примером применения спирали Архимеда являются направляющие для кулачков, зажимающих детали в патроне токарного станка.

Рис. 12

Эвольвенты также относятся к спиралям. Они, как и спираль Архимеда, имеют две ветви в зависимости от направления развертывания.

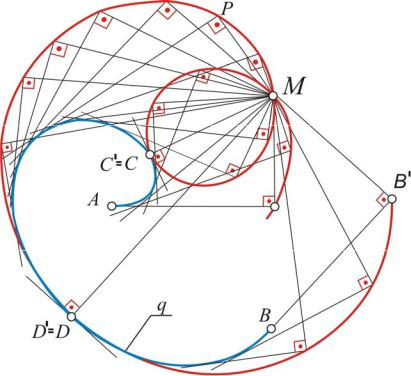
На практике используют и спирали, составленные из дуг окружностей, проводимых из двух, трех и более центров, расположенных в вершинах правильных многоугольников. Такие спирали называют завитками. На рис. 13

показана спираль с двумя центрами – О1 и О2. На рис. 14 приведен пример использования четырехцентрового завитка в очертании кожуха вентилятора.

1.3. ПОДЕРЫ

Подерой (греч. podos – нога) данной плоской кривой называют множество оснований перпендикуляров, опущенных из какой-либо точки плоскости (полюса) кривой на касательные к ней (рис. 15).

Рис. 15

Любая кривая (называемая в этом случае антиподерой) имеет бесчисленное множество подер, вид которых зависит от выбора полюса.

Свойство подер используется при решении различных технических и геометрических задач.

1.4.КРИВЫЕ ЛИНИ В ПРИРОДЕ (ЖУК-ГЕОМЕТР)

Вприроде можно встретить закономерные кривые линии. В работе [21] приведен пример использования эволюты жучками-листовертами. Для своего потомства они свертывают из листьев (березы, винограда) домики в виде тру-

бочек конической формы. Чтобы домики были прочными, трубочки должны быть аккуратными, иметь ровные края, их не должны растрепать ветры и ливни. Но как свернуть из листьев, имеющих неровные края, такую трубочку?

Будем рассуждать. Если бы лист имел форму круга, то трубочку с ровными краями можно было бы сделать очень просто: надо разрезать его по радиусу и свернуть (рис. 16).

Рис. 16

Трубочка получится очень аккуратная: ведь она представляет собой коническую поверхность, у которой все образующие равны, они имеют размер радиуса одного и того же круга.

Возьмем теперь лист, ограниченный не окружностью, а какой то другой кривой, например такой, как показано на рис. 17.

Рис. 17

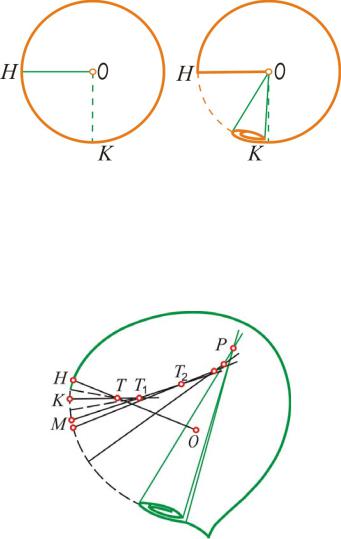
Если взять произвольную точку О внутри контура листа, сделать разрез по линии ОН и свернуть трубочку, то она получится плохой, потому что образующие конической поверхности будут разной длины.

Возьмем теперь какую-нибудь точку K на краю листа. Примем контур листа между точками H и K за дугу окружности и найдем центр этой окружности. С этой целью проведем в точках Н и K нормали к окружности. Точка Т пересечения нормалей будет искомым центром. Теперь рассмотрим контур листа между точками K и М. Его тоже можно без большой погрешности считать дугой окружности, но центр этой окружности не совпадает с центром в точке Т. Проведя нормали к контуру листа в точках K и М, мы найдем точку их пересе-

чения Т1, не совпадающую с точкой Т. Поступая таким же образом и дальше,

получим точку Т2 и вообще – целый ряд центров, около которых нужно заворачивать лист, чтобы получить аккуратную трубочку.

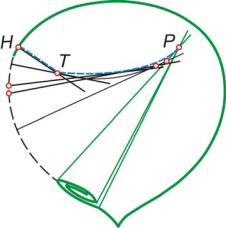
Если заменить ломаную линию Т Т1 Т2 … плавной кривой, как это показано на рис. 18, то будет получена огибающая нормалей, проведенных из точек на кромке листа, а это, как мы знаем, является эволютой кромки (контура) листа. Значит, для того чтобы свернуть из листа наиболее аккуратную трубочку, нужно предварительно разрезать лист по отрезку прямой HТ (нормали), а затем – по эволюте ТР его контура. И вот жучок-листоверт (жуки из родов Rhynchites, Byctiscus и др.) прекрасно решает сложную математическую задачу. Он прогрызает лист по эволюте контура и лишь после этого свертывает его. На рис. 19 изображен березовый листоверт и разрезанный им лист. На рис. 20 изображен увеличенный виноградный листоверт и его трубочка.

Рис. 18