Если поместить шарик в произвольную точку М и предоставить самому себе, то он начнет совершать колебания, причем период этих колебаний не будет зависеть от выбора точки М. Если даже под влиянием трения и сопротивления воздуха размах колебаний будет уменьшаться, время колебания маятника останется неизменным. Гюйгенс доказал, что часы с обыкновенным круговым маятником не могут идти точно. Применение в часовых механизмах равномерности движения маятника по циклоиде позволило создать самые точные часы, которые до появления атомных часов обеспечивали службу времени в астрономических обсерваториях.

Если подвижная центроида будет двигаться не по прямой линии, а по окружности, то получатся другие виды циклоид. Они называются эпициклоидами или гипоциклоидами в зависимости от того, по наружной или внутренней стороне окружности перекатывается подвижная центроида.

Окружность, обкатывающая внешнюю сторону направляющей окружности, образует эпициклоиды, внутреннюю – гипоциклоиды. Способы их построения и проведения к ним касательных и нормалей в общем случае такие же, как и для циклоиды, с тем лишь отличием, что длину обкатывающей окружности откладывают на направляющей.

В зависимости от соотношения между радиусами неподвижной и подвижной окружностей будут получаться различные, хотя и родственные кривые.

Эпициклоиды

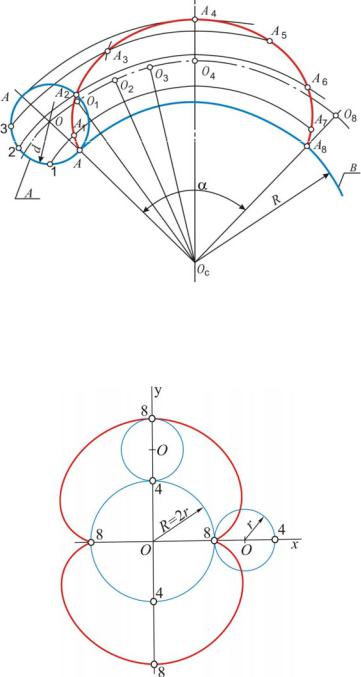
Эпициклоидой называется траектория точки некоторой окружности А (производящей) (рис. 4), перекатывающейся без скольжения по неподвижной окружности В (направляющей) с наружной стороны. Центральный угол α определяется по формуле

α =180° DR .

Уравнения эпициклоиды:

x = (R + r)cos ϕ – r cos R r+r ϕ; y = (R + r)sin ϕ – r sin R r+r ϕ,

где R – радиус направляющей окружности; r – радиус производящей окружности; ϕ – угол поворота производящей окружности.

Рис. 4

Если радиус производящей окружности вдвое меньше радиуса окружности направляющей, то получится кривая с двумя остриями – «точками возврата»

(рис. 5).

Рис. 5

Если это соотношение меньше в три, четыре или шесть раз, то получатся кривые с соответствующим количеством точек возврата.

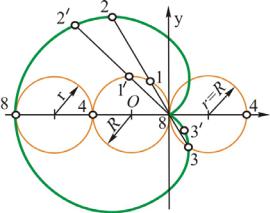
Если радиусы производящей и направляющей окружностей одинаковые, то получается эпициклоида с одной аркой, которая называется кардиоидой (рис. 6). Слово «кардиоида» означает по-гречески «сердцевидная».

Рис. 6

Для любого луча, выходящего из точки 8, справедливо равенство 1–2 = = 1′−2′= 1–3 = 1′−3′… = 2r. На этом основан простой способ построения кардиоиды: проводят лучи и на них откладывают от точек 1, 1′, … по обе стороны отрезки, равные 2r.

Уравнения кардиоиды:

x = r(2cos ϕ – cos 2ϕ);

y = r(2sin ϕ – sin 2ϕ),

где r – радиус производящей и направляющей окружностей; ϕ – угол поворо-

та производящей окружности.

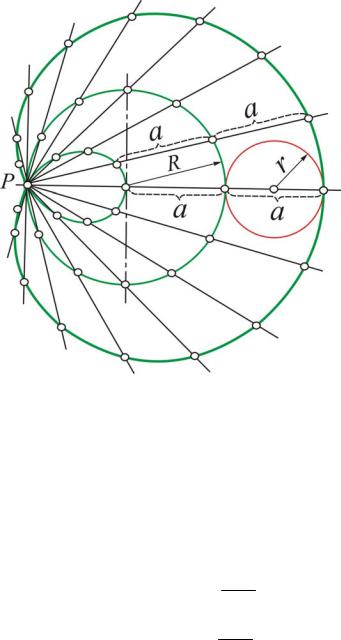
Удлиненные (r > R) и укороченные (r < R, рис. 7) эпициклоиды могут слу-

жить улитками Паскаля.

Улитка Паскаля иначе называется конхоидой окружности. Построения аналогичны построению кардиоиды. Если радиусы производящей и направляющей окружностей одинаковые, то улитка Паскаля превращается в кардиоиду.

Рис. 7

Пример применения улиток Паскаля – очертания эксцентриков, преобразующих вращательное движение в прямолинейное возвратно-поступательное.

Гипоциклоиды

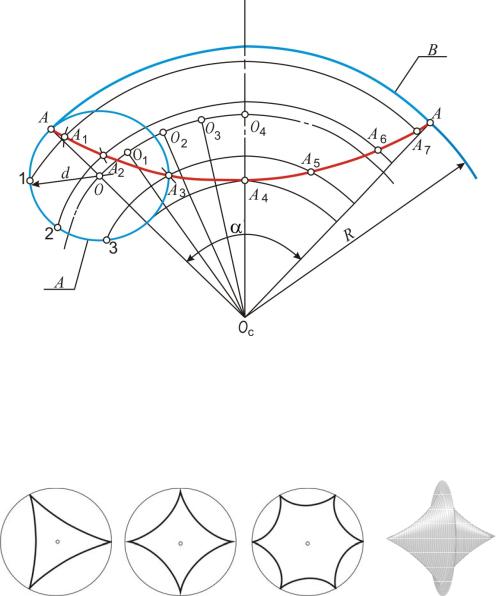
Гипоциклоидой называется траектория точки некоторой производящей окружности А (рис. 8), перекатывающейся без скольжения (внутреннее касание) по неподвижной направляющей окружности В.

Уравнения гипоциклоиды:

x = (R – r)cos ϕ + r cos R r−r ϕ; y = (R – r)sin ϕ – r sin R r−r ϕ,

где R – радиус направляющей окружности; r – радиус производящей окружности; ϕ – угол поворота производящей окружности.

Рис. 8

Если радиус подвижной окружности будет в два, три, вообще в n раз меньше радиуса неподвижной, то получится гипоциклоида с двумя, тремя, вообще с n заострениями.

На рис. 9, а–в изображены гипоциклоиды с тремя, четырьмя и шестью заострениями. Гипоциклоида с четырьмя заострениями называется астроидой.

На рис. 10 изображено тело, ограниченное поверхностью, порожденной вращением астроиды вокруг отрезка, соединяющего ее противоположные острия.