Все кривые на конусе, полученные в результате сечения, – это результат проецирования окружности на эти плоскости. Любая кривая – это проекция любой другой кривой, т. е. в проективной геометрии они ничем по своим свойствам не отличаются друг от друга. Однако на чертежах они имеют разные размеры.

На рис. 21 показано:

•плоскость δ пересекает все образующие конуса, она не параллельна ни одной из образующих, фигура сечения – эллипс;

•плоскость β параллельна одной из образующих, фигура сечения –

парабола;

• плоскость γ параллельна сразу двум образующим, фигура сечения – гипербола.

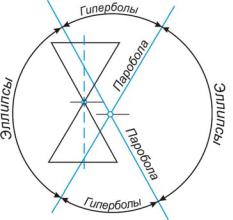
Рис. 22

Заметим, что ни одна из секущих плоскостей не проходит через точку S. Удаляя вершину конуса в «бесконечность», будем приближать образующие

к взаимной параллельности. В пределе точка S исчезнет, а конус обратится в цилиндр. Его сечения те же, но не будет параболы и гиперболы. Схема образования конических сечений показана на рис. 22.

13. ПРОЕКЦИИ КРИВЫХ ЛИНИЙ

Ортогональное проецирование переводит алгебраическую кривую порядка n в алгебраическую кривую того же порядка, т. е. порядок плоской алгебраической кривой при ее ортогональном проецировании сохраняется.

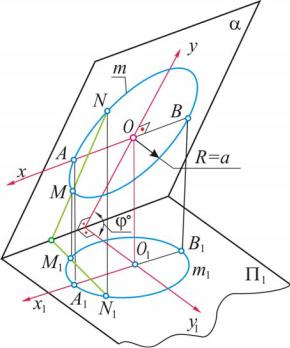
Рассмотрим ортогональную проекцию кривой m второго порядка – окружности, плоскость α которой составляет с плоскостью П1 угол ϕ° (рис. 23).

Рис. 23

Диаметр окружности АВ параллелен плоскости П1 и поэтому проецируется на нее в натуральную величину. Все хорды, перпендикулярные АВ, сокращаются в cos ϕ раз. Так, M1N1 = MN cos ϕ. Очевидно, проекция окружности есть

эллипс с большой осью А1В1 и коэффициентом сжатия cos ϕ. В самом деле, в системе xOy (Ox||П1) окружность m определяется уравнением x2 + y2 = a2 , а

так как x = x1 (O1x1||Ox) и y = y1: cos ϕ, то

Итак, ортогональная проекция окружности радиусом а есть эллипс с полуосями а и аcos ϕ.

Аналогично можно показать, что ортогональная проекция эллипса есть эллипс, гиперболы – гипербола, параболы – парабола. Или: аффинный класс кривой второго порядка сохраняется при ортогональном проецировании.

14. ЭЛЛИПС – ФИГУРА, РОДСТВЕННАЯ ОКРУЖНОСТИ

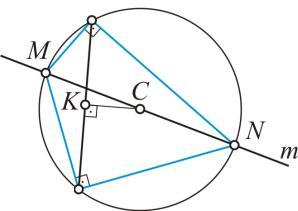
В родственном соответствии двух плоскостей, заданных осью m и двумя родственными точками А1 и А2, можно построить два взаимно перпендикулярных направления одной из плоскостей, соответствующих двум взаимно перпендикулярным направлениям другой плоскости. Такие направления называются главными в данном родственном соответствии. Построение показано на рис. 24.

А1

А2

Рис. 24

Отрезок прямой А1А2 разделен пополам в точке K, и через эту точку проведен перпендикуляр к А1А2 до пересечения с m в точке С. Из точки С проведена окружность через точки А1 и А2. Получены две пары родственных прямых:

А1М и А2М, А1N и A2N. Углы МА1N и MA2N – прямые.

Фигура, родственная окружности, – эллипс, причем взаимно перпендикулярные диаметры окружности переходят в сопряженные диаметры эллипса.

Рассмотрим построение эллипса, когда направление родства перпендикулярно к оси родства.

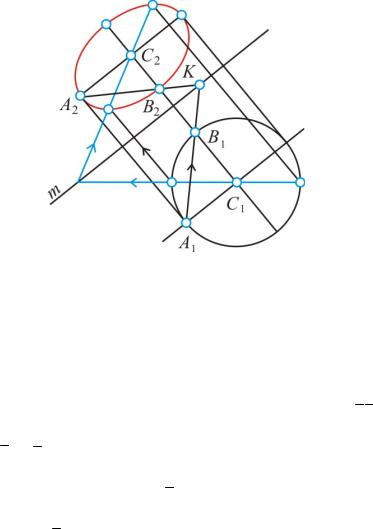
Пусть даны ось родства m и две родственные точки С1 и С2, причем точка С1 является центром окружности (рис. 25).

Рис. 25

Направление родства C1C2 расположено перпендикулярно к оси. Построим фигуру, родственную окружности, – эллипс с центром С2. Полуоси эллипса А2С2 и B2C2 построим как прямые, родственные двум взаимно перпендикулярным радиусам A1C1 и B1C1.

Рассмотрим еще пример родственных соответствий. Пусть даны оси эллипса АВ и СD (рис. 26). Большую ось АВ совместим с диаметром АB родственной окружности и примем за ось родства m. Точки C и D эллипса соответствуют точкам С и D окружности.

Из центра О радиусом ОС проведем окружность, а на родственной окружности отметим произвольную точку М . Из этой точки проведем прямую, перпендикулярную к оси m. Это направление родства.

Соединим точку М с точкой О прямой линией, отметим точку K пересечения этой линии с окружностью радиуса ОС, из которой проведем прямую, параллельно большой оси эллипса до пересечения с направлением родства в точке М, точка М принадлежит эллипсу. Другие точки эллипса строятся аналогично. Таким образом, эллипс – фигура, родственная окружности.