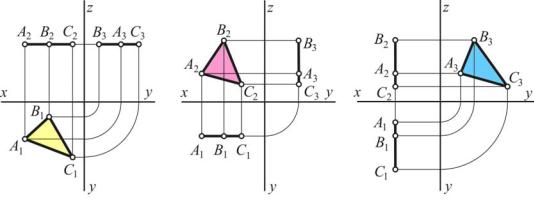
Плоскость уровня

Плоскость, параллельная одной из плоскостей проекций и, следовательно, перпендикулярная к двум другим, называется плоскостью уровня. Она имеет только два следа. Оба следа обладают собирательным свойством и потому являются следами-проекциями. Существует три вида плоскостей уровня: гори-

зонтальная, фронтальная и профильная. Они параллельны плоскостям П1, П2,

П3 соответственно. На рис. 1 верхняя грань AA2AzA3 параллелепипеда является горизонтальной плоскостью, передняя грань AA1AyA3 – фронтальной, а левая

грань AA1AxA2 – профильной. На рис. 30 показаны эпюры таких плоскостей с находящимися на них фигурами-треугольниками.

ВЫВОДЫ

1.Прямая линия, не параллельная ни одной из плоскостей проекций, называется прямой общего (произвольного) положения.

2.Точки пересечения прямой с плоскостями проекций называются сле-

дами.

3.Аналитическое задание прямой может быть выражено как линия пересечения двух плоскостей, полученная решением системы двух линейных уравнений (уравнений плоскостей), каноническим уравнением для прямой, проходящей через определенную точку пространства в направлении заданного вектора, в векторной форме и др.