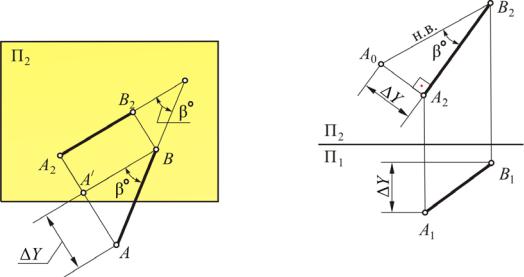
Рис. 18

Определите самостоятельно угол наклона троса АВ к вертикальной стене в приведенной выше задаче.

3. ВЗАИМНОЕ ПОЛОЖЕНИЕ ДВУХ ПРЯМЫХ

Различают три варианта взаимного положения двух прямых: пересекающиеся, параллельные и скрещивающиеся.

Пересекающиеся прямые

Пересекающиеся прямые имеют одну общую точку (рис. 19, а). На эпюре точки пересечения одноименных проекций находятся на одном перпендикуляре к соответствующей оси проекций. Пересекающиеся прямые лежат в одной плоскости.

Если прямые линии пересекаются под произвольным углом и не параллельны плоскости проекций, то плоский угол между ними проецируется на плоскость проекций с искажением.

Если прямые линии пересекаются под произвольным углом и параллельны плоскости проекций, то плоский угол между ними проецируется на плоскость проекций без искажения.

Рис. 19

Прямой угол между двумя пересекающимися прямыми проецируется на плоскость без искажения, если хотя бы одна сторона этого угла параллельна плоскости проекций. На рис. 19, б у прямого угла ABC сторона AB параллельна

горизонтальной плоскости проекций, в результате чего на эту плоскость угол проецируется без искажения. На рис. 19, в прямой угол ABC проецируется на фронтальную плоскость проекций без искажения, так как одна его сторона (BС) параллельна плоскости проекций.

Параллельные прямые

Параллельные прямые лежат в одной плоскости и пересекаются в несобственной точке. Признаком параллельности прямых является параллельность их одноименных проекций на всех плоскостях проекций. Для задания параллельных прямых общего положения достаточно двух проекций (рис. 20, а), но если эти прямые являются прямыми частного положения, то становится необходимым построение третьей проекции. Такое построение показано на рис. 20, б для двух профильных прямых. Видно, что, несмотря на параллельность двух проекций, прямые не являются параллельными.

Скрещивающиеся прямые

Скрещивающиеся прямые не параллельны и не пересекаются между собой. Они не лежат в одной плоскости, поэтому на эпюре точки пересечения их од-

ноименных проекций не лежат на одном перпендикуляре к соответствующей оси проекций, так как это проекции разных точек (рис. 21).

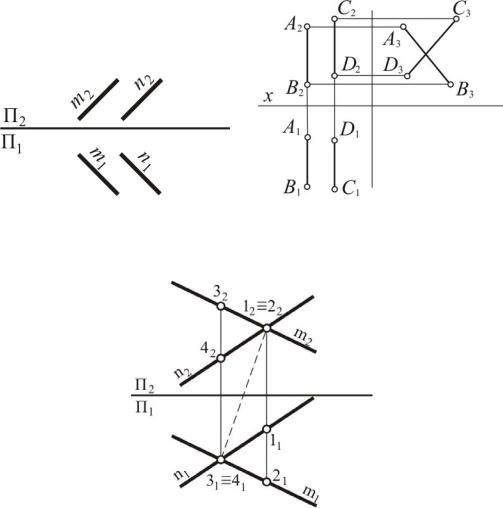
Рис. 20

Рис. 21

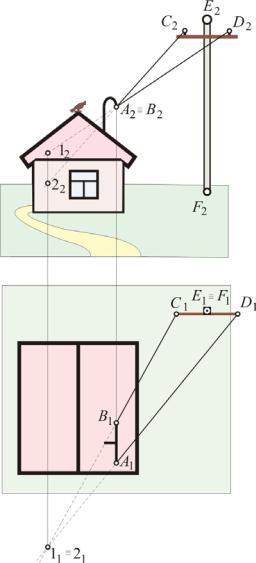
К дачному домику (рис. 22) электрик провел электрические провода, один из которых натянут между местами крепления в точках В и С, а другой – между А и D. Допустим, что есть необходимость убедиться в безопасности их взаимного расположения. Тогда для исключения возможного касания проводов надо определить минимальное расстояние между ними.

Рис. 22

Натянутые провода в данном случае являются скрещивающимися прямыми (если не учитывать их провисание), и определение минимального расстояния между ними решается методами начертательной геометрии.