1.4.3. Вычитание с использованием двоичного дополнения. Умножение

Вся теория будет строиться сначала для десятичных чисел.

Десятичным дополнениемn-разрядного числаназывается разность. Например, десятичное дополнение числа 7 – 3, числа 342 – 658, числа 007 – 993.

Идея использования десятичного дополнения при вычитании основана на следующих рассуждениях. Пусть необходимо найти разность . Возможны случаи:

а) . В этом случае рассмотрим тождество, откуда следует правило нахождения разности:

– найти десятичное дополнение к вычитаемому;

– сложить найденное дополнение и уменьшаемое;

– зачеркнуть единицу старшего разряда и вместо нее поставить знак «+»;

б) . В этом случае используем тождество, или, если черезобозначить сумму, получим

.

Отсюда следует, что искомая разность есть десятичное дополнение к числу, взятое со знаком «–».

Приведенные рассуждения позволяют сформулировать следующий алгоритм.

Алгоритм вычитания целых десятичных чисел

Шаг 1. Уравнять число разрядов в числахи, приписав впереди требуемое число нулей.

Шаг 2. Найти десятичное дополнение вычитаемого

.

Шаг 3. Найти сумму.

Шаг 4. Если появилась единица в дополнительном старшем разряде числа, то заменить ее знаком «+».В противном случае найти десятичное дополнение числаи поставить перед ним знак «–».

Шаг 5. Полученное число считать искомой разностью.

Заметим, что алгоритм не требует предварительного сравнения уменьшаемого и вычитаемого.

Пример 7.Найти разность.

1. ;. Находим дополнение числа 39, имеем. Складываем уменьшаемое и найденное дополнение:. Отбрасываем единицу старшего разряда и получаем 35 (или 74 – 39=35).

2. ;. Находим дополнение числа 47:. Складываем уменьшаемое и найденное дополнение:. Так как единица в старшем разряде не появилась, то находим десятичное дополнение числа 76:, берем его со знаком минус и считаем искомой разностью:.

Приведенные рассуждения и основанный на них алгоритм могут быть построены и в позиционной системе счисления с натуральным основанием, отличным от десяти. Однако наиболее эффективен такой подход к вычитанию в двоичной арифметике. Объясняется это тем, что в этой системе счисления очень просто находится «двоичное дополнение» (двоичным дополнением n-значного числаявляется разность).

Алгоритм отыскания двоичного дополнения числа

Шаг 1. Все единицы числазаменить нулями, а все нули – единицами.

Шаг 2. К полученному числу по правилам двоичной арифметики прибавить 1.

Чтобы получить алгоритм вычитания двоичных чисел, достаточно в приведенном выше алгоритме заменить слово «десятичный» словом «двоичный», а индекс «10» заменить индексом «2».

Пример 8.Найти разность.

,	;
Находим двоичное дополнение вычитаемого
Находим сумму
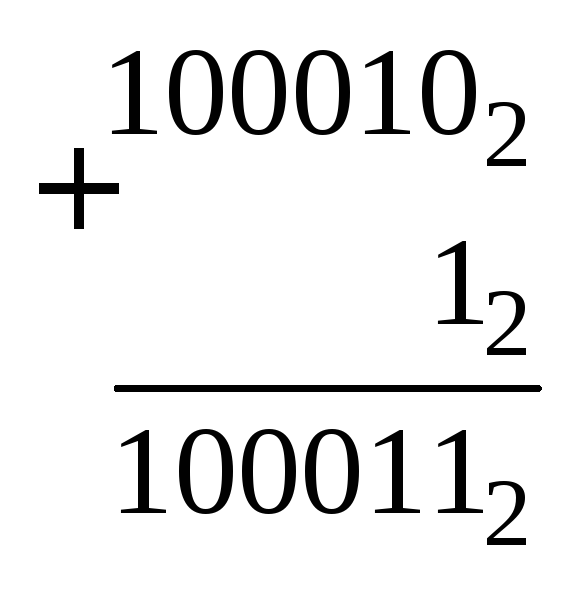
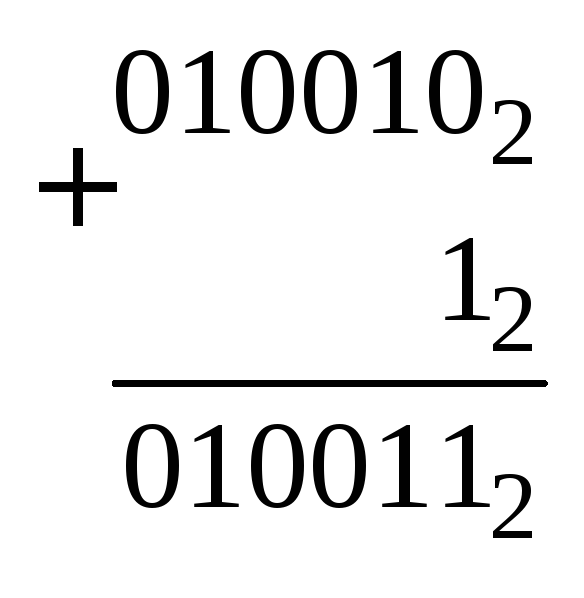
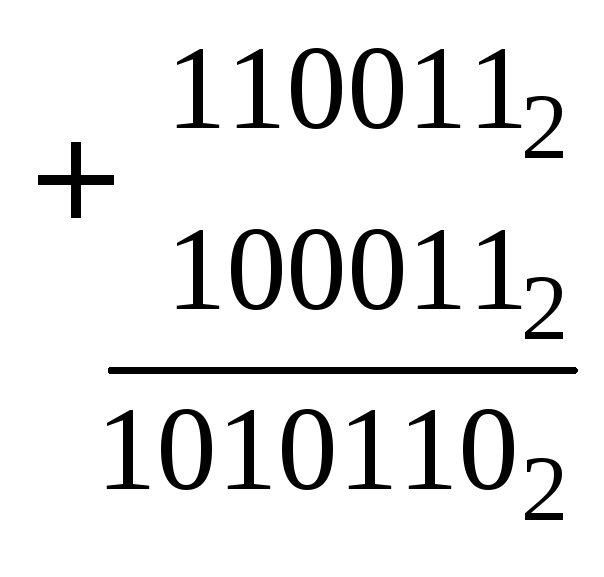
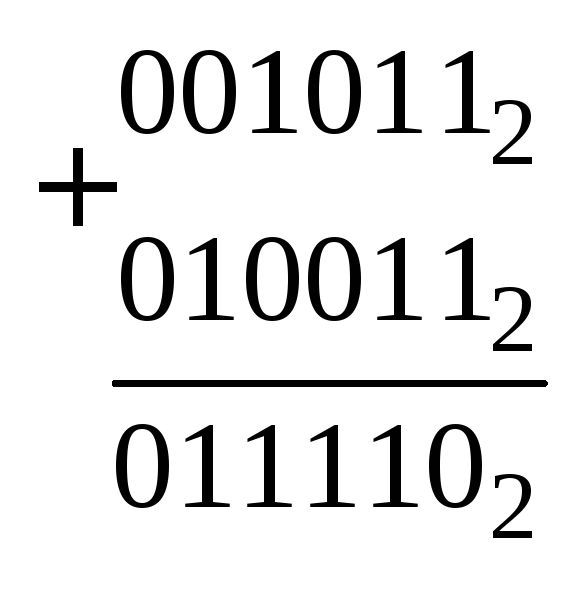
В соответствии с алгоритмом отбрасываем единицу в дополнительном старшем разряде	Так как число 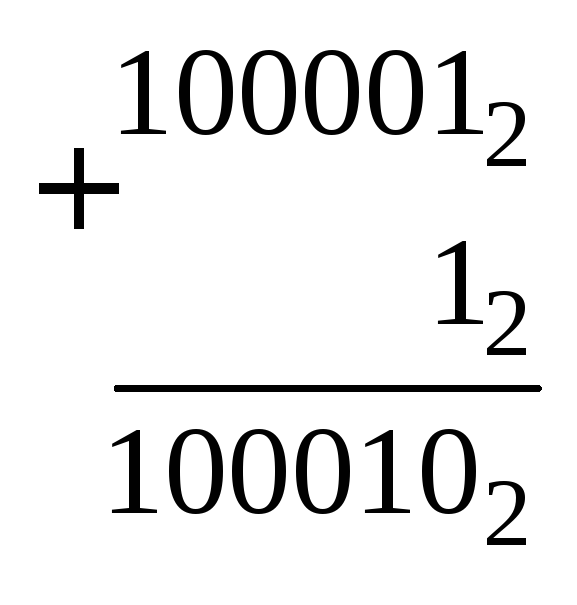содержит столько же разрядов, что и числаи, то в соответствии с алгоритмом находим дополнение числа: . Найденное дополнение берётся со знаком минус