1.3. Взаимосвязь систем счисления
Из недесятичных систем счисления с натуральным основанием наибольшее распространение в настоящее время получили системы счисления с основанием, равным двум, восьми и шестнадцати (однако в современной математике находят применение и другие системы счисления).
Современные ЭВМ используют двоичную и шестнадцатеричную системы счисления, а человек в повседневной практике пользуется десятичной системой счислений. Поэтому, чтобы глубоко понимать, как работает ЭВМ, необходимо знать алгоритмы перевода чисел из одной системы счисления в другую.
Для облегчения запоминания договоримся под d-ичной системой понимать десятичную, а подq-ичной любую другую систему счисления (алгоритмы работоспособны и без этого ограничения).
I. Алгоритм перевода целого числа Aq из q-ичной системы счисления в число Bd d-ичной системы
Присвоить результату цифру старшего разряда.
Если цифры закончились – stop.
Умножить текущее значение результата на «старое» основание qпо правиламd-арифметики.
Прибавить цифру следующего разряда и перейти на шаг 2.
Пример
1.Число
заменить равным ему десятичным числом.
II. Алгоритм перевода целого числа Ad из d-ичной системы счисления в число Bq q-ичной системы
Разделить «с остатком» по правилам d-ичной арифметики числоAdна числоq, записанное вd-ичной системе.
Если результат q, то повторить пункт 1.
Записать результат деления как цифру q-ичной системы. Это будет цифра старшего разряда искомого числаBq. Далее выписать последовательно остатки от делений, начиная с последнего, записанные как цифрыq-ичной системы.
Пример 2. Число 157 заменить равным ему числом в системе счисления с основаниема) q=4,б) q=16.
,
,
,
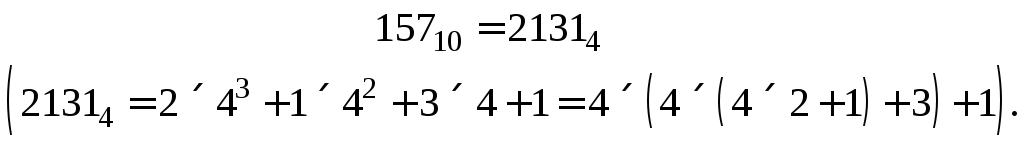
б)
157=9
16+13=9
16+D,
.
III. Алгоритм перевода правильных дробей из q-ичной системы счисления в d-ичную с вычислениями в d-ариф-метике
Цифру младшего разряда числа 0,Aqразделить с требуемой точностью на «старое» основаниеqпо правиламd-арифметики.
Если цифры закончились – stop.
Прибавить следующую цифру исходной дроби.
Текущее значение результата разделить на «старое» основание qпо правиламd-арифметики и перейти на шаг 2).
Пример
3.Представить в десятичной системе
счисления с точностью 4 знака после
запятой а)
;
б)
;
в)
.
а)
Ответ:
б)
Ответ:
в)
Ответ:
IV. Алгоритм перевода правильных дробей из d-ичной системы счисления в q-ичную с вычислениями в d-арифметике
Умножить по правилам d-арифметики исходную дробь 0,Adна «новое» основаниеq, записанное вd-ичной системе.
Целую часть полученного произведения считать цифрой старшего разряда искомой дроби.
Если дробная часть равна 0 или достигнута требуемая точность, то stop. Иначе, дробную часть полученного произведения умножить по правиламd‑арифметики на «новое» основаниеq, записанное вd-ичной системе и перейти на шаг 2.
Пример
4.
Получить двоичное представление дроби
а)
;
б)
.
а) 
.
Ответ:
б) 
Ответ:
V. Алгоритм перевода чисел из d-ичной системы счисления в dn-ичную систему счисления
1. Разбить целую часть числа справа налево, а дробную часть слева направо на группы по nцифр. При необходимости добавить слева и справа от числа незначащие нули.
2. Каждое получившееся n-значное число заменить цифройdn-ичной системы счисления.
Пример 5.
,
