I. Системы счисления

Впервые числовые термины появились как качественные, а не как количественные. Они показывали лишь различие между одним и многими. Качественное разделение на единственное и множественное число и по сей день присутствует почти во всех разговорных языках.

Система счисления– это совокупность приемов обозначения (записи) чисел. Системы счисления подразделяют напозиционныеинепозиционные. В позиционной системе счисления значение каждой цифры в изображении числа зависит от ее положения в последовательности цифр, изображающих число.

1.1. Непозиционные системы счисления. Римская система счисления

Большинство непозиционных систем являлись аддитивными, т.е. числа в них образовывались путем сложения: 3 = 2+1, 4 = 2+2.

Примеры древних аддитивных непозиционных систем счисления

1. Камиларои считали: 1 = мал, 2 = булан, 3 = гулиба, 4 = булан-булан и так далее.

2. Унарная система счисления.Простейшая система счисления – зарубки или палочки. В этой системе счисления удобно складывать, но она очень громоздка. Сейчас используется для обучения счету.

3. Древнеегипетская иероглифическая система счисления (2,5 в. до н.э.):

|– единица,– десять,С– сотня.

4. Древнегреческая система счисления – числа, 1, 2, …, 9, 10, 20, …, 90, 100, 200… обозначались буквами с чертой сверху. Позже эта традиция через Византию пришла вдревнеславянскуюписьменность.

5. Древнеримская аддитивная система счисления: ключевые числа 1, 5, 10, 50, 100, 500, 1000 обозначалисьI,V,X,L,C,DиM. (V– одна пятерня,X– две пятерни,C–centum,D–demilleиM–mille).

Современная Римская системасчисления, отличается от древнеримской только тем, что не является чисто аддитивной.

Правило получения значения числа в современной Римской системе:если меньшая цифра стоит перед большей, то ее надо вычитать из общего значения числа, в противном случае прибавлять к общему значению числа.

Недостатками всех непозиционных систем являются громоздкость и сложность вычислений.

1.2. Позиционные системы счисления

Древнейшая позиционная система счисления была в Вавилоне. Ее возраст 2…3 тысячи лет.

Цифры: – 1,– 10. Основание: 60.

Первоначально употреблялась для записи денежных единиц (1 мина серебра = 60 шекелям, 1 талант = 60 минам). В этой системе счисления первоначально не было 0, поэтому числа 1, 60, 3600 выглядели одинаково. Кроме того, в этой системе не было знака, отделяющего дробную и целую части. Тем не менее эта система счисления дошла до наших дней – с ее помощью определяется время.

Система счисления индейцев племени майя:

Цифры: – 1,–– 5. Ключевые числа: 1, 20, 18·20, 18·20², …

Система счисления дошла до наших дней в виде градусной меры угла.

Принцип поместного значения цифр и их начертание зародились в Индии в VIв. В Европе они стали известны лишь вIXв. благодаря книге хорезмского математика Мухаммеда ибн Муса. Книга была написана на арабском языке и поэтому цифры называются арабскими. Иногда эти цифры называются индийскими. В России с индийской нумерацией познакомились только вXIIIв. ВXVIIв. вошла в употребление современная алгебраическая символика (знаки «=», «+», «–» и др.).

В дальнейшем будем рассматривать d-ичные позиционные системы счисления, основание которых –d, а цифры – натуральные числа от 0 доd–1.

Записать число в d-ичной системе счисления означает: представить это число либо в цифровой

,

либо в многочленной

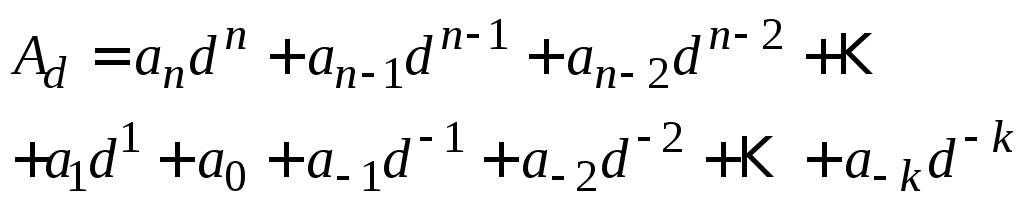
формах.