- •Оглавление
- •Глава 3. Логика высказываний 78
- •Глава 4. Логика предикатов 90
- •Введение
- •I. Системы счисления
- •1.1. Непозиционные системы счисления. Римская система счисления
- •1.2. Позиционные системы счисления
- •1.3. Взаимосвязь систем счисления
- •I. Алгоритм перевода целого числа Aq из q-ичной системы счисления в число Bd d-ичной системы
- •II. Алгоритм перевода целого числа Ad из d-ичной системы счисления в число Bq q-ичной системы
- •III. Алгоритм перевода правильных дробей из q-ичной системы счисления в d-ичную с вычислениями в d-ариф-метике
- •IV. Алгоритм перевода правильных дробей из d-ичной системы счисления в q-ичную с вычислениями в d-арифметике
- •V. Алгоритм перевода чисел из d-ичной системы счисления в dn-ичную систему счисления
- •VI. Алгоритм перевода чисел из dn-ичной системы счисления в d-ичную систему счисления.
- •1.4. Двоичная система счисления
- •1.4.1. Двоичная арифметика
- •1.4.3. Вычитание с использованием двоичного дополнения. Умножение
- •Алгоритм вычитания целых десятичных чисел
- •Алгоритм отыскания двоичного дополнения числа
- •Теория множеств
- •Глава 1. Множества
- •1.1. Основные определения
- •1.2. Основные операции теории множеств
- •Старшинство операций (операции даны по убыванию приоритетов)
- •1.4. Диаграммы Венна
- •1.5. Основные законы теории множеств
- •1.6. Декартово произведение и отношения
- •Глава 2. Бинарные отношения
- •2.1. Основные определения
- •Глава 3.Функции и операции
- •Примеры функций
- •Операции над функциями
- •Свойства бинарных операций
- •Глава 4.Алгебраические структуры
- •III. Математическая логика
- •Глава 1. Переключательные функции
- •1.1. Основные определения
- •Переключательные функции двух аргументов
- •1.2. Основные теоремы (эквивалентные соотношения) переключательных функций
- •Глава 2.Булева алгебра
- •2.1. Основные определения
- •Эквивалентные соотношения в булевой алгебре
- •2.2. Минимизация булевых функций
- •2.3. Аналитические методы нахождения мднф Метод Квайна
- •Формулы метода
- •Алгоритм метода
- •Метод Блейка
- •Формулы метода
- •Алгоритм метода
- •Сравнение методов Квайна и Блейка
- •Построение мднф из Сокр.Днф с помощью таблицы Квайна
- •Алгоритм получения fМднФс помощью таблицы Квайна
- •2.4. Графическая минимизация логических функций
- •Метод карт Карнапа
- •Алгоритм минимизации по карте Карнапа
- •2.5. Полнота систем булевых функций
- •Классы Поста
- •Полиномы Жегалкина
- •Глава 3.Логика высказываний
- •3.1. Основные понятия
- •3.2. Алгебра логики высказываний
- •3.3. Применение к естественному языку
- •Список наиболее часто встречающихся выражений, соответствующих логическим связкам
- •3.4. Исчисление высказываний (ив)
- •Глава 4.Логика предикатов
- •Определения кванторных высказываний
- •4.1. Алгебра логики предикатов
- •4.2. Выполнимость и общезначимость
- •4.3. Равносильность формул
- •Приведенные формулы
- •4.4. Применение логики предикатов к естественному языку
- •4.4.1. Суждения
- •Виды категорических суждений
- •4.4.2. Исчисление одноместных предикатов как исчисление классов. Теория категорических суждений и силлогизмов Аристотеля
- •Законы формальной логики Аристотеля:
- •4.4.3. Умозаключения
- •Наиболее распространенные схемы правильных дедуктивных рассуждений
- •4.4.4. Основные законы формальной логики. Логические основы аргументации
- •4.5. Исчисление предикатов
- •Литература
- •Предметный указатель
Глава 3.Функции и операции
Бинарное
отношение fназываетсяn-местной функцией
(функциональным отношением,
однозначным отношением), действующей
из![]() вB(
вB(![]() ),
если
),
если![]() ,
,![]() и для всех
и для всех![]() ,y1,y2из того, что
,y1,y2из того, что![]() и
и![]() ,
следует
,
следует![]() .
Если f функция,
то вместо
.
Если f функция,
то вместо![]() принято писать
принято писать![]() ,
при этомyназываютзначениемфункцииfпри значенияхаргументовx1,x2, …, xn.
Если
,
при этомyназываютзначениемфункцииfпри значенияхаргументовx1,x2, …, xn.
Если![]() ,
то функцию называют всюду определенной,
в противном случаечастично определенной.
,
то функцию называют всюду определенной,
в противном случаечастично определенной.
Функция
fназываетсяинъекцией,
если для всехx1,x2из того, что![]() ,
следует, что
,
следует, что![]() .
.
Функция
fназываетсясюръекцией,
если![]() .
.
Функция fназываетсябиекцией (взаимно однозначным соответствиеммежду множествамиAиB), если она является инъекцией и сюръекцией одновременно.
Если
функция
![]() всюду определена, то говорят, что «fестьотображение A
в B», если кроме
этогоf– сюръекция,
то говорят, что «fестьотображение A
на B». Отображение
всюду определена, то говорят, что «fестьотображение A
в B», если кроме
этогоf– сюръекция,
то говорят, что «fестьотображение A
на B». Отображение![]() часто называютпреобразованием
множестваA, если
при этом отображение является функцией,
то говорят, что «f–перестановка наA».
часто называютпреобразованием
множестваA, если
при этом отображение является функцией,
то говорят, что «f–перестановка наA».
Преобразование
f дискретного
конечного множестваA={1,2,3}
обычно записывается следующим образом:![]() или
или![]() .
Такая запись задает функцию, значение
которой равно 2 для аргумента 1, 3 – для
аргумента 2 и 1 – для аргумента 3.
.
Такая запись задает функцию, значение
которой равно 2 для аргумента 1, 3 – для
аргумента 2 и 1 – для аргумента 3.
Функции fи gравны, если:
совпадают их области определения;
для любого элемента aиз области определения
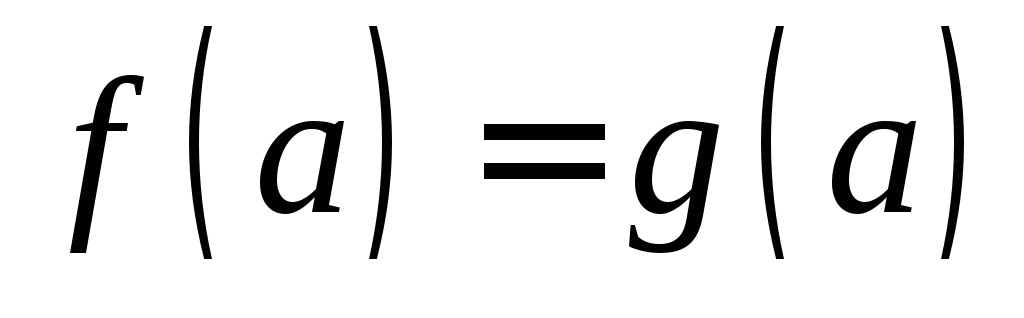 .
.
Два множества AиBимеют одну и ту жемощность(кардинальное число), если существует взаимно однозначное соответствие между элементами этих множеств. В этом случае говорят, чтоAиBэквивалентны(обозначаютAB).Aестьбесконечное множество, если оно имеет ту же мощность, что и хотя бы одно из его собственных подмножеств; в противном случаеA–конечное множество. Каждое кардинальное число конечного множества тождественно с числом его элементов.
Бесконечное множество Aсчётно, если можно установить взаимно однозначное соответствие между ним и множеством натуральных чисел.
Характеристической
функцией множестваAназывается
функция: ![]()
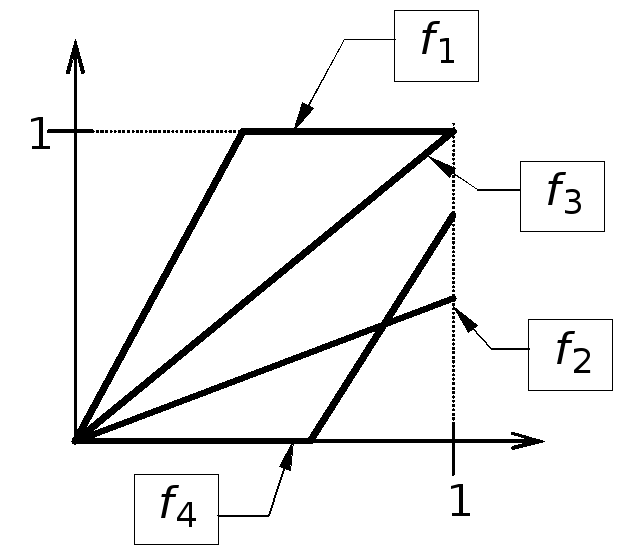
Примеры функций
|
1) fi :[0,1][0,1] f1– сюръекция, не инъекция; f2– инъекция, не сюръекция; f3– биекция; f4– не сюръекция, не инъекция; 2)
Функция
|
|
Операции над функциями
1.
Функция
![]() называетсяобратной функциейк
функции
называетсяобратной функциейк
функции![]() .
Для функции
.
Для функции![]() обратная функция существует тогда и
только тогда, когдаfявляется взаимно однозначным соответствием
между своими областями определения и
значений. Заметим, что функция по
определению есть отношение, значит,
определено обратное отношение, но,
возможно, что оно не является функцией.
обратная функция существует тогда и
только тогда, когдаfявляется взаимно однозначным соответствием
между своими областями определения и
значений. Заметим, что функция по
определению есть отношение, значит,
определено обратное отношение, но,
возможно, что оно не является функцией.
2.
Функция
![]() называетсякомпозициейфункций
называетсякомпозициейфункций![]() и
и![]() (обозначается
(обозначается![]() ),
если имеет место равенство
),
если имеет место равенство![]() .
.
Часто
говорят, что функция h
полученаподстановкой fвg. Для многоместных
функций![]() ,
,![]() возможны различные варианты подстановкиfвg.
возможны различные варианты подстановкиfвg.
3.
Функция, полученная из
![]() некоторой подстановкой их друг в друга
и переименованием аргументов, называетсясуперпозицией
некоторой подстановкой их друг в друга
и переименованием аргументов, называетсясуперпозицией
![]() .
Выражение, описывающее эту суперпозицию
и содержащее функциональные знаки,
скобки и символы аргументов, называетсяформулой суперпозиции.
.
Выражение, описывающее эту суперпозицию
и содержащее функциональные знаки,
скобки и символы аргументов, называетсяформулой суперпозиции.
Пример
21.Пусть![]() ,
,![]() ,
,![]() ,
,![]() ,
тогда:
,
тогда:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Функция
![]() есть суперпозиция функцийfиg, формула которой
есть суперпозиция функцийfиg, формула которой![]() .
.
Пример 22.Пусть дано множествоA={1,2,3,4} и два преобразования этого множества
![]() ,
,
![]() ,
,
тогда композиции этих преобразований:
![]() ,
,
![]() .
.
Операциейназывают функцию, все аргументы и
значения которой принадлежат одному и
тому же множеству. В общем случаеn-местная функция![]() называетсяn-арной
операциейна множествеA(иногда говорят, что «у операцииарностьравнаn).
В таких случаях говорят, что множествоAзамкнуто относительно
операции(результат
выполнения операциинаAпринадлежитA).
В частности, функция одного аргумента
называетсяунарной операцией, а
двух аргументов –бинарной операцией.
называетсяn-арной
операциейна множествеA(иногда говорят, что «у операцииарностьравнаn).
В таких случаях говорят, что множествоAзамкнуто относительно
операции(результат
выполнения операциинаAпринадлежитA).
В частности, функция одного аргумента
называетсяунарной операцией, а
двух аргументов –бинарной операцией.

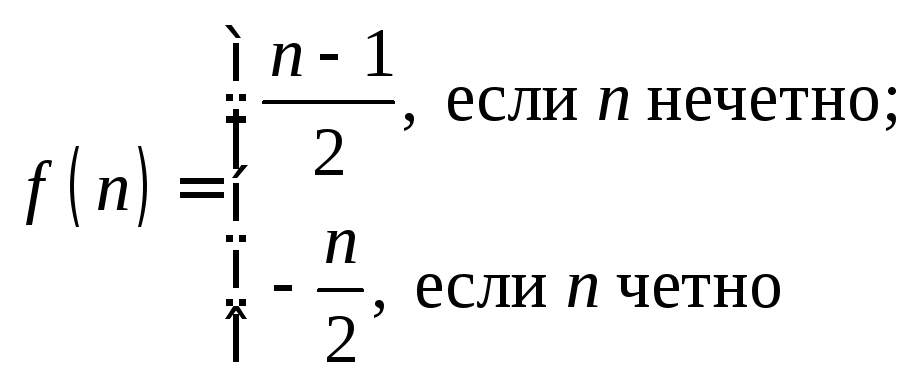 есть биекция между
множествами N
и Z.
есть биекция между
множествами N
и Z.