
- •Вводное занятие
- •1. Случайные и систематические погрешности. Меры погрешности
- •2. Оценка случайных погрешностей прямых многократных измерений
- •3. Математическая обработка результатов прямых многократных измерений
- •4. Оценка погрешностей прямого однократного измерения и косвенных измерений
- •5. Предварительная подготовка к выполнению лабораторных работ
- •6. Оформление протокола лабораторной работы
- •7. Построение графиков
- •8. Задание к вводному занятию
- •9. Контрольные вопросы к вводному занятию
- •Литература
- •Лабораторная работа № 1 измерение времени соударения упругих тел
- •1. Описание установки и эксперимента
- •2. Зависимость времени соударения от размера шаров
- •3. Задания
- •4. Контрольные вопросы
- •Литература
- •Лабораторная работа № 2 измерение начальной скорости пули с помощью баллистического маятника
- •1. Описание установки и эксперимента
- •2. Измерение скорости пули
- •3. Зависимость скорости пули от ее массы
- •4. Оценка стандартного отклонения величины
- •5. Задания
- •6. Контрольные вопросы
- •Литература
- •Лабораторная работа № 3 изучение вращательного движения маятника обербека
- •1. Описание установки и эксперимента
- •2. Зависимость углового ускорения маятника от массы ускоряющего груза
- •3. Измерение углового ускорения
- •4. Задания
- •5. Контрольные вопросы
- •Литература
- •Лабораторная работа № 4 определение момента инерции маятника обербека
- •1. Зависимость момента инерции маятника от расстояния грузов до оси вращения
- •2. Измерение момента инерции маятника
- •3. Оценка стандартного отклонения момента инерции
- •4. Задания
- •5. Контрольные вопросы
- •Литература
- •Лабораторная работа № 5 определение отношения теплоемкостей методом клемана и дезорма
- •1. Описание метода Клемана и Дезорма
- •2. Описание экспериментальной установки
- •3. Измерение
- •4. Оценка стандартного отклонения величины γ
- •5. Теоретическое значение
- •6. Задания
- •Контрольные вопросы
- •Литература
- •Лабораторная работа № 6 определение коэффициента внутреннего трения (вязкости) жидкости по методу стокса
- •1. Теория эксперимента
- •2. Задания
- •3. Описание эксперимента
- •4. Задание к работе
- •6 30092, Г. Новосибирск, пр. К. Маркса, 20
Лабораторная работа № 1 измерение времени соударения упругих тел
В данной работе проводится измерение времени упругого соударения двух одинаковых стальных шаров с помощью секундомера.
Целью работы является сравнение экспериментально полученной зависимости времени соударения шаров от диаметра шара с теоретической.
1. Описание установки и эксперимента
Два
металлических шара, радиусы и массы
которых одинаковы, подвешены на проводящих
нитях (см. рис. 1, вводное занятие).
Один шар отводится в сторону (при этом
поднимается на высоту
![]() )
до соприкосновения с электромагнитом.
При отключении электромагнита с помощью
тумблера «ПУСК» шар 1 падает и происходит
соударение. При этом шары замыкают
электрическую цепь. В процессе соударения
(в течение времени контакта шаров) в
цепи протекает импульсный ток. В
электрическую цепь, состоящую из
генератора периодических импульсов,
соединительных проводов (на них и
подвешены шары) и стальных шаров, включен
также счетчик импульсов (выполняет роль
секундомера). Время прохождения
импульсного тока (фактически – количество
прошедших за время контакта электрических
импульсов в цепи) считается временем
соударения (удара) шаров.
)
до соприкосновения с электромагнитом.
При отключении электромагнита с помощью
тумблера «ПУСК» шар 1 падает и происходит
соударение. При этом шары замыкают
электрическую цепь. В процессе соударения
(в течение времени контакта шаров) в
цепи протекает импульсный ток. В
электрическую цепь, состоящую из
генератора периодических импульсов,
соединительных проводов (на них и
подвешены шары) и стальных шаров, включен
также счетчик импульсов (выполняет роль
секундомера). Время прохождения
импульсного тока (фактически – количество
прошедших за время контакта электрических
импульсов в цепи) считается временем
соударения (удара) шаров.
2. Зависимость времени соударения от размера шаров
Рассмотрим движение шаров в двух инерциальных системах отсчёта (ИСО): в лабораторной системе отсчёта (ЛСО) и в системе центра инерции (СЦИ).
В
лабораторной системе отсчета (ЛСО) шар
![]() ,
начиная двигаться с высоты
,
начиная двигаться с высоты![]() ,
к моменту соударения приобретает
скорость, которую обозначим
,
к моменту соударения приобретает
скорость, которую обозначим![]() .
При этом импульс шара в ЛСО равен
.
При этом импульс шара в ЛСО равен![]() .
Заметим, что шар 1 всегда начинает
двигаться с одинаковой высоты
.
Заметим, что шар 1 всегда начинает
двигаться с одинаковой высоты![]() ,
равной разности уровней электромагнита
и покоящегося шара. Поэтому скорость
налетающего шара в момент соударения
не изменяется от соударения к соударению:
,
равной разности уровней электромагнита
и покоящегося шара. Поэтому скорость
налетающего шара в момент соударения
не изменяется от соударения к соударению:![]() .
Шар
.
Шар![]() до соударения находится в покое. Из
законов сохранения импульса и механической
энергии для центрального упругого удара
одинаковых шаров следует, что после
соударения шар
до соударения находится в покое. Из
законов сохранения импульса и механической
энергии для центрального упругого удара
одинаковых шаров следует, что после
соударения шар![]() остановится, а шар
остановится, а шар![]() получит импульс
получит импульс![]() .
Изменение импульса шара 2 за время
соударения
.
Изменение импульса шара 2 за время
соударения![]() .
.
Из
второго закона Ньютона
![]() для времени соударения имеем
для времени соударения имеем
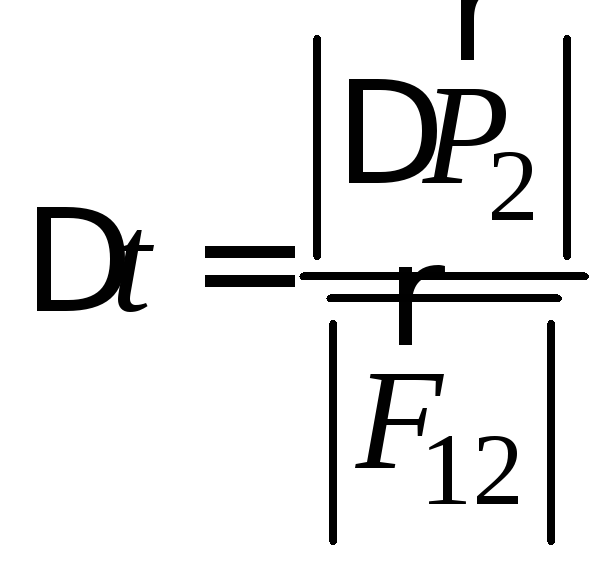 , (1)
, (1)
где
![]() – среднее (за время соударения) значение
модуля упругой силы, с которой первый
шар действует на второй. Обозначим это
среднее значение буквой
– среднее (за время соударения) значение
модуля упругой силы, с которой первый
шар действует на второй. Обозначим это
среднее значение буквой![]() ,
а время соударения шаров – буквой
,
а время соударения шаров – буквой![]() ,
тогда
,
тогда
![]() .
.
В
нерелятивистском случае
![]() и
и![]() одинаковы во всех ИСО. Следовательно,
и
одинаковы во всех ИСО. Следовательно,
и![]() тоже одинаковы во всех ИСО. При решении
конкретной задачи выбирают такую ИСО,
в которой решение наименее громоздко.
Для определения
тоже одинаковы во всех ИСО. При решении
конкретной задачи выбирают такую ИСО,
в которой решение наименее громоздко.
Для определения![]() мы рассмотрим соударение шаров в системе
центра инерции (СЦИ), называемой также
системой центра масс. Радиус-вектор
центра инерции системы двух материальных
точек определяется по формуле
мы рассмотрим соударение шаров в системе
центра инерции (СЦИ), называемой также
системой центра масс. Радиус-вектор
центра инерции системы двух материальных
точек определяется по формуле![]() ,
где
,
где![]() –
массы и радиусы-векторы точек
соответственно. Отсюда для скорости
движения центра инерции относительно
ЛСО имеем:
–
массы и радиусы-векторы точек
соответственно. Отсюда для скорости
движения центра инерции относительно
ЛСО имеем:![]() ;
при
;
при![]() ,
,![]() ,
,![]() получаем
получаем![]() .
.
Определим
скорости шаров до и после удара в СЦИ.
Из теоремы сложения скоростей Галилея
следует, что скорость относительного
движения тела
![]() (относительно движущейся системы
отсчёта) равна разности абсолютной
скорости движения этого тела
(относительно движущейся системы
отсчёта) равна разности абсолютной
скорости движения этого тела![]() (относительно
неподвижной системы отсчёта) и скорости
переносного движения (скорости движущейся
системы отсчёта относительно неподвижной)
(относительно
неподвижной системы отсчёта) и скорости
переносного движения (скорости движущейся
системы отсчёта относительно неподвижной)![]() :
:
![]() .
.
В
нашем случае абсолютной скоростью
является скорость шара в ЛСО, относительной
– в СЦИ, а переносной – скорость СЦИ в
ЛСО
![]() .
.
Для
первого шара до удара скорость в СЦИ
есть
![]() ,
а для второго шара
,
а для второго шара![]() .
.
Обозначим
импульсы первого и второго шаров в СЦИ
до удара
![]() и
и![]() ,
а после соударения –
,
а после соударения –![]() и
и![]() .
Закон сохранения импульса в СЦИ имеет
вид:
.
Закон сохранения импульса в СЦИ имеет
вид:
![]() . (2)
. (2)
Следовательно,
![]() ;
;![]() .
.
Если
соударение упругое, то кинетические
энергии шаров до
и после соударения
равны (закон сохранения энергии):
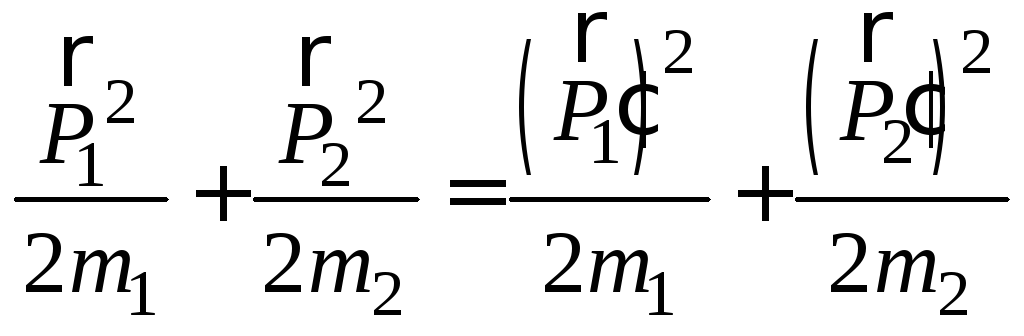 ,
или
,
или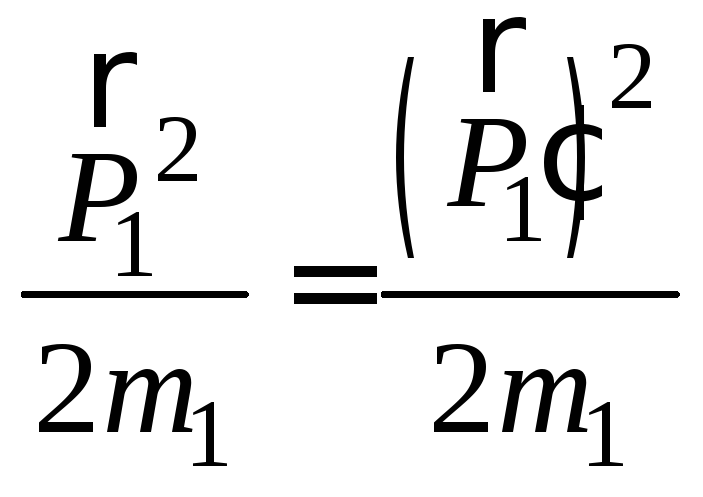 .
В этом случае
.
В этом случае![]() ,
,![]() .
.
Шары взаимодействуют друг с другом с упругими силами, равными по величине и противоположными по направлению (третий закон Ньютона). Процесс упругого соударения шаров в СЦИ можно представить в виде следующих двух этапов:
на первом этапе оба шара одновременно тормозятся и упруго деформируются, пока кинетическая энергия шаров полностью не превратится в энергию упругой деформации;
на втором этапе величина упругой деформации
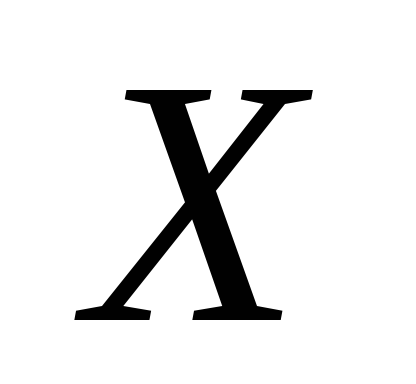 уменьшается до нуля, энергия упругой
деформации превращается в кинетическую
энергию шаров.
уменьшается до нуля, энергия упругой
деформации превращается в кинетическую
энергию шаров.
Закон сохранения механической энергии для первого этапа соударения шаров имеет вид:
![]() ,
т. е.
,
т. е.
![]() ,
(3)
,
(3)
где
![]() – максимальная величина продольной
деформации, одинаковая для каждого из
шаров. Отсюда средняя величина упругой
силы
– максимальная величина продольной
деформации, одинаковая для каждого из
шаров. Отсюда средняя величина упругой
силы
![]() . (4)
. (4)
Подставляя
в (1) это выражение (напомним, что мы ввели
обозначение
![]() ),
получаем, что время соударения шаров
),
получаем, что время соударения шаров
![]() . (5)
. (5)
Из
(5) следует, что
![]() пропорционально
пропорционально![]() .
.
Для
определения зависимости
![]() от радиуса
от радиуса![]() необходимо найти зависимость
необходимо найти зависимость![]() от
от![]() .
Для этого рассмотрим сначала грубую
физическую модель, в которой шар диаметром
.
Для этого рассмотрим сначала грубую
физическую модель, в которой шар диаметром![]() заменен телом кубической формы с ребром
заменен телом кубической формы с ребром![]() (
(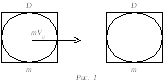 рис. 1).
рис. 1).
Считаем,
что при упругом соударении двух стальных
кубов, когда при соударении соприкасающиеся
грани идеально совпадают, упругая сила
пропорциональна величине деформации
(закон Гука):
![]() ,
где
,
где![]() – коэффициент жёсткости. В иной форме
закон Гука можно записать:
– коэффициент жёсткости. В иной форме
закон Гука можно записать:
![]() ,
(6)
,
(6)
где
![]() – модуль Юнга;
– модуль Юнга;![]() – площадь поперечного сечения
деформируемого тела. Из (6) следует, что
– площадь поперечного сечения
деформируемого тела. Из (6) следует, что
![]() .
(7)
.
(7)
Закон сохранения механической энергии для первого этапа соударения можно записать так:
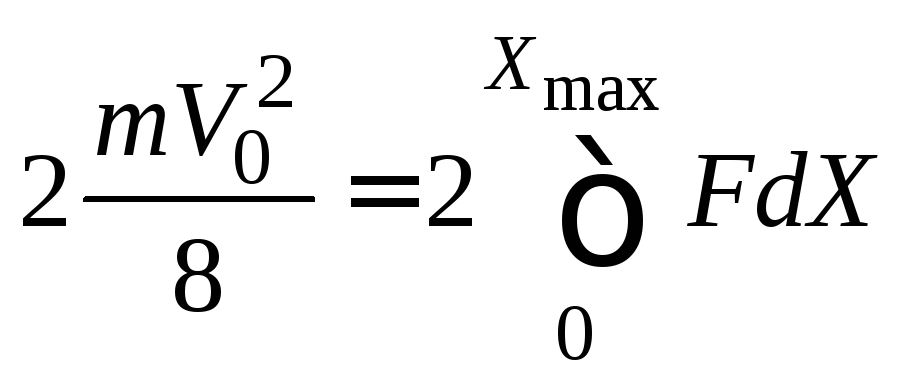 .
.
Подставим
![]() из (7), тогда:
из (7), тогда: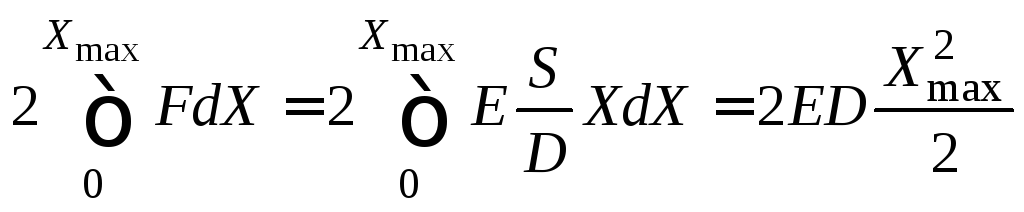 ,
отсюда
,
отсюда![]() и
и![]() .
Так как
.
Так как![]() ,
где
,
где![]() – плотность тела, а
– плотность тела, а![]() – его объём (для куба
– его объём (для куба![]() ),
получаем:
),
получаем:
![]() . (8)
. (8)
Подставляя
найденное выражение для
![]() в формулу (5), для времени соударения
кубических тел получаем
в формулу (5), для времени соударения
кубических тел получаем
![]() . (9)
. (9)
Закон
Гука в виде (6) справедлив лишь для
равномерно сжатого вдоль одного из
рёбер прямоугольного параллелепипеда
(или цилиндра). Для шара картина
принципиально другая. В этом случае
зависимость
![]() от величины продольной деформации
является нелинейной:
от величины продольной деформации
является нелинейной:
![]() , (10)
, (10)
где
![]() .
.
Из
(10) следует, что
![]() растет быстрее, чем величина деформации
растет быстрее, чем величина деформации![]() ;
это случай так называемой системы с
жесткой характеристикой.
;
это случай так называемой системы с
жесткой характеристикой.
В этом случае закон сохранения механической энергии для первого этапа соударения шаров можно записать так:
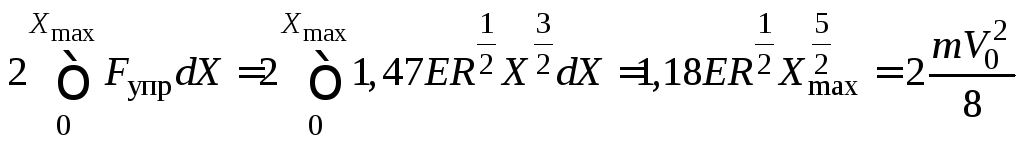 .
.
Учитывая,
что для шара
![]() ,
для
,
для![]() получаем
получаем
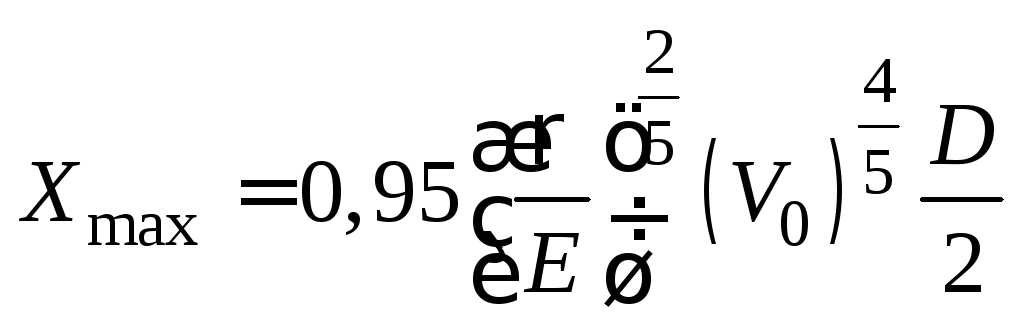 . (11)
. (11)
Подставляя
найденное выражение для
![]() в формулу (5), для времени соударения
шаров получаем:
в формулу (5), для времени соударения
шаров получаем:
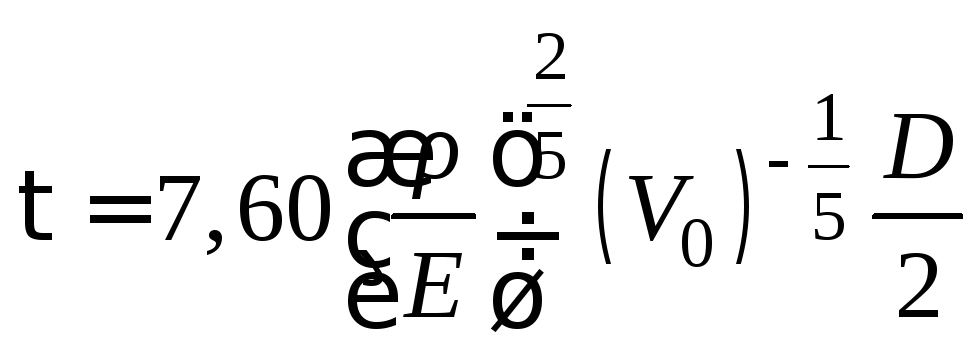 . (12)
. (12)
Следовательно,
для стальных шаров в рамках модели
системы с жёсткой характеристикой, так
же как и для тел кубической и цилиндрической
формы, максимальная величина продольной
деформации
![]() пропорциональна размерам тел – радиусу
пропорциональна размерам тел – радиусу![]() .
То есть обе модели приводят к линейной
зависимости времени соударения стальных
шаров от их диаметра:
.
То есть обе модели приводят к линейной
зависимости времени соударения стальных
шаров от их диаметра:
![]() , (13)
, (13)
где
![]() – коэффициент пропорциональности,
который в случае модели двух цилиндров
(кубов) равен
– коэффициент пропорциональности,
который в случае модели двух цилиндров
(кубов) равен![]() ,
а в случае системы с жёсткой характеристикой
,
а в случае системы с жёсткой характеристикой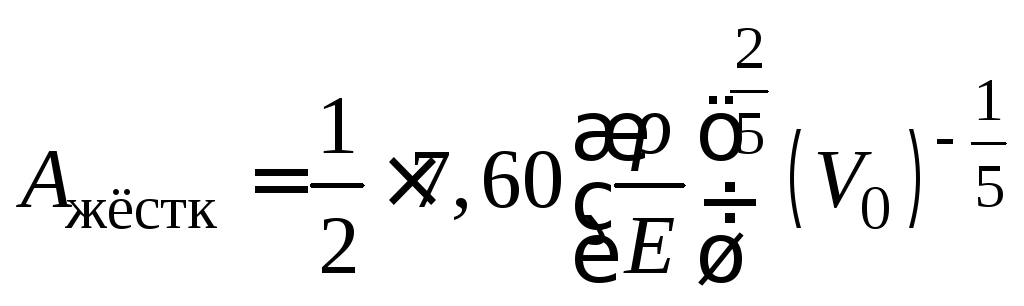 .
.
Именно
эту теоретически полученную зависимость
(13)
![]() от
от![]() необходимо подтвердить (или опровергнуть)
экспериментально, измеряя время
соударения шаров микросекундометром.
При этом следует ответить на вопрос:
какая из двух рассмотренных выше моделей
более адекватно описывает соударение
реальных шаров. Значения диаметров
шаров приведены в паспорте установки.
необходимо подтвердить (или опровергнуть)
экспериментально, измеряя время
соударения шаров микросекундометром.
При этом следует ответить на вопрос:
какая из двух рассмотренных выше моделей
более адекватно описывает соударение
реальных шаров. Значения диаметров
шаров приведены в паспорте установки.
