
- •Вводное занятие
- •1. Случайные и систематические погрешности. Меры погрешности
- •2. Оценка случайных погрешностей прямых многократных измерений
- •3. Математическая обработка результатов прямых многократных измерений
- •4. Оценка погрешностей прямого однократного измерения и косвенных измерений
- •5. Предварительная подготовка к выполнению лабораторных работ
- •6. Оформление протокола лабораторной работы
- •7. Построение графиков
- •8. Задание к вводному занятию
- •9. Контрольные вопросы к вводному занятию
- •Литература
- •Лабораторная работа № 1 измерение времени соударения упругих тел
- •1. Описание установки и эксперимента
- •2. Зависимость времени соударения от размера шаров
- •3. Задания
- •4. Контрольные вопросы
- •Литература
- •Лабораторная работа № 2 измерение начальной скорости пули с помощью баллистического маятника
- •1. Описание установки и эксперимента
- •2. Измерение скорости пули
- •3. Зависимость скорости пули от ее массы
- •4. Оценка стандартного отклонения величины
- •5. Задания
- •6. Контрольные вопросы
- •Литература
- •Лабораторная работа № 3 изучение вращательного движения маятника обербека
- •1. Описание установки и эксперимента
- •2. Зависимость углового ускорения маятника от массы ускоряющего груза
- •3. Измерение углового ускорения
- •4. Задания
- •5. Контрольные вопросы
- •Литература
- •Лабораторная работа № 4 определение момента инерции маятника обербека
- •1. Зависимость момента инерции маятника от расстояния грузов до оси вращения
- •2. Измерение момента инерции маятника
- •3. Оценка стандартного отклонения момента инерции
- •4. Задания
- •5. Контрольные вопросы
- •Литература
- •Лабораторная работа № 5 определение отношения теплоемкостей методом клемана и дезорма
- •1. Описание метода Клемана и Дезорма
- •2. Описание экспериментальной установки
- •3. Измерение
- •4. Оценка стандартного отклонения величины γ
- •5. Теоретическое значение
- •6. Задания
- •Контрольные вопросы
- •Литература
- •Лабораторная работа № 6 определение коэффициента внутреннего трения (вязкости) жидкости по методу стокса
- •1. Теория эксперимента
- •2. Задания
- •3. Описание эксперимента
- •4. Задание к работе
- •6 30092, Г. Новосибирск, пр. К. Маркса, 20
3. Математическая обработка результатов прямых многократных измерений
Г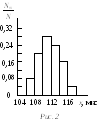 истограмма.
Гистограмма – это ступенчатый график
зависимости относительной частоты
попадания результатов измерений
истограмма.
Гистограмма – это ступенчатый график
зависимости относительной частоты
попадания результатов измерений![]() в выбранный интервал от величины
результата измерений
в выбранный интервал от величины
результата измерений![]() (рис. 2). Каждому интервалу соответствует
столбик. Для построения гистограммы
сначала представим результаты измерений
в табл. 2. Здесь
(рис. 2). Каждому интервалу соответствует
столбик. Для построения гистограммы
сначала представим результаты измерений
в табл. 2. Здесь![]() – номер интервала,
– номер интервала,![]() –
ширина интервала,
–
ширина интервала,![]() – количество измерений, результаты
которых приходятся на интервал номер
– количество измерений, результаты
которых приходятся на интервал номер![]() .
.
Опишем
процедуру заполнения табл. 2 подробнее.
Сначала следует определить количество
интервалов
![]() .
Оно должно соответствовать количеству
измерений в серии примерно так:
.
Оно должно соответствовать количеству
измерений в серии примерно так:![]() .
При
.
При![]() получим
получим![]() .
Но можно выбрать близкое число: 6 или
8. Выберем
.
Но можно выбрать близкое число: 6 или
8. Выберем![]() .
.
Следующий
шаг – определение ширины интервалов
![]() .
Величину
.
Величину![]() определяют по формуле
определяют по формуле![]() .
Пусть, например,
.
Пусть, например,![]() мкс,
мкс,![]() мкс, тогда
мкс, тогда![]() мкс.
мкс.
Определение
границ интервалов производим так. Левая
граница первого интервала –
![]() ,
правая –
,
правая –![]() .
В первую строчку (
.
В первую строчку (![]() )
второго столбца таблицы записываем:
106 – 108. Во вторую строчку:
)
второго столбца таблицы записываем:
106 – 108. Во вторую строчку:![]() –
–![]() .
И т. д. Последняя строчка (
.
И т. д. Последняя строчка (![]() )
может быть заполнена так:
)
может быть заполнена так:![]() –
–![]() ,
т. е. в нашем примере 116 – 118.
,
т. е. в нашем примере 116 – 118.
Используя
второй столбец таблицы, определяем
количество измерений, попавших в каждый
интервал
![]() ,
и заполняем остальные столбцы.
,
и заполняем остальные столбцы.
Результат измерения, попавший точно на границу между интервалами, следует относить всегда к левому либо всегда к правому интервалу. Результаты подсчётов представим в виде табл. 2.
|
Таблица 2 |
Таблица 2а | |||||||
|
|
Интервалы |
|
|
|
|
Интервалы |
|
|
|
мкс |
мкс | |||||||
|
|
|
|
|
1 |
106 – 108 |
4 |
0,08 | |
|
|
|
|
|
2 |
108 – 110 |
10 |
0,2 | |
|
|
|
|
|
3 |
110
–
|
14 |
0,28 | |
|
|
|
|
|
4 |
|
12 |
0,24 | |
|
|
|
|
|
5 |
|
8 |
0,16 | |
В нашем конкретном примере таблица имеет вид (табл. 2а) (допустимо интервалы записывать в виде: нижняя граница – (тире) – верхняя граница):
Пусть,
например, в 1-й интервал, между
![]() и
и![]() попало 4 измерения, во 2-й 10 измерений
и т.д. Необходимо проверить, равна ли
сумма всех
попало 4 измерения, во 2-й 10 измерений
и т.д. Необходимо проверить, равна ли
сумма всех![]() полному числу измерений
полному числу измерений![]() .
.
Подсчитаем
относительную частоту попадания в![]() -й
интервал
-й
интервал![]() для каждого интервала и запишем её в
последний столбец таблицы. Очевидно,
сумма всех относительных частот равна
единице.
для каждого интервала и запишем её в
последний столбец таблицы. Очевидно,
сумма всех относительных частот равна
единице.
По
табл. 2а строим гистограммув осях![]() и
и![]() (рис. 2). Для этого над каждым интервалом
строим прямоугольник высотой
(рис. 2). Для этого над каждым интервалом
строим прямоугольник высотой![]() (ширина прямоугольника равна
(ширина прямоугольника равна![]() ).
).
Теоретическая
плотность вероятности. Если все
ординаты![]() на рис. 2 разделить на
на рис. 2 разделить на![]() ,изменится только вертикальный масштаб
гистограммы, который выбирается
произвольно из соображений удобства.
(Мы могли сразу откладывать на оси
ординат величину
,изменится только вертикальный масштаб
гистограммы, который выбирается
произвольно из соображений удобства.
(Мы могли сразу откладывать на оси
ординат величину![]() и при соответствующем выборе масштаба
получить вид гистограммы, в точности
совпадающий с приведённым на рис. 2.)
Эта преобразованная гистограмма при
и при соответствующем выборе масштаба
получить вид гистограммы, в точности
совпадающий с приведённым на рис. 2.)
Эта преобразованная гистограмма при![]() и
и![]() (обозначим
(обозначим![]() )
перейдет в плавную кривую
)
перейдет в плавную кривую![]() (рис. 3):
(рис. 3):
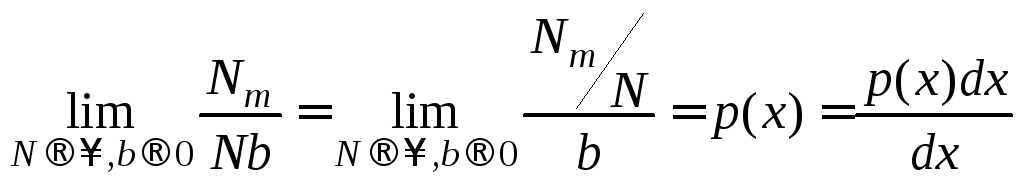 .
.
Поскольку
![]() переходит в
переходит в![]() ,
относительная частота попаданий
,
относительная частота попаданий![]() переходит в
переходит в![]() .
Поэтому вероятность попадания результата
в интервал
.
Поэтому вероятность попадания результата
в интервал![]() равна
равна![]() ,
а вероятность
,
а вероятность![]() попадания результата в конечный интервал
попадания результата в конечный интервал![]() находится интегрированием:
находится интегрированием:
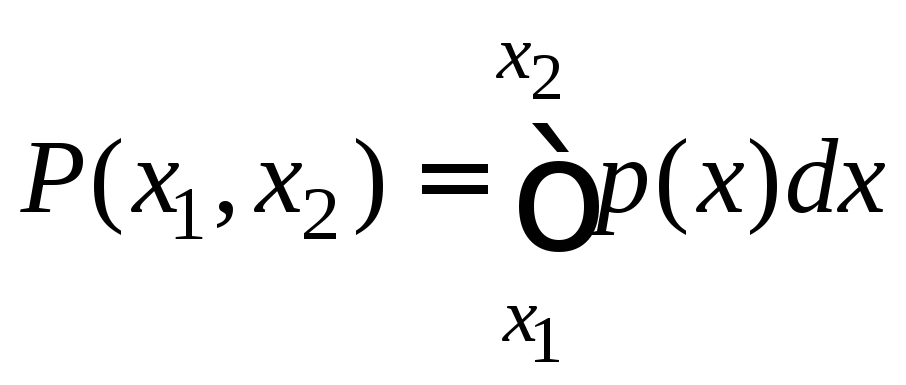 .
.
Вероятность
![]() можно рассматривать как функцию верхнего
предела
можно рассматривать как функцию верхнего
предела![]() .
Очевидно, что эта функция является
дифференцируемой и
.
Очевидно, что эта функция является
дифференцируемой и
![]() .
.
Поэтому
функция
![]() называетсяплотностью распределения
вероятностейили простоплотностью
вероятностей.
называетсяплотностью распределения
вероятностейили простоплотностью
вероятностей.
Геометрической
интерпретацией вероятности
![]() попадания результата в конечный интервал
попадания результата в конечный интервал![]() является площадь под кривой
является площадь под кривой![]() на соответствующем интервале
на соответствующем интервале![]() .
Полная площадь под кривой
.
Полная площадь под кривой![]() равна
единице как вероятность достоверного
события.
равна
единице как вероятность достоверного
события.
В реальных физических экспериментах всегда существует много независимых причин возникновения погрешностей, каждая из которых слабо влияет на общий результат. В этом случае, независимо от природы и характера этого влияния, результаты многократных измерений имеют вид так называемого нормального распределения(илираспределения Гаусса):
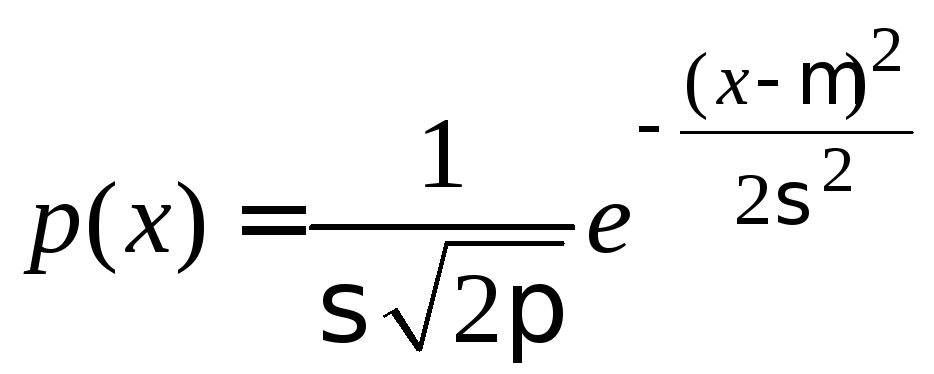 .
(2)
.
(2)
Зависимость
![]() для нормального распределения (2)
представлена на рис. 3.
для нормального распределения (2)
представлена на рис. 3.
Свойства нормального распределения (рис. 3):
существует наиболее вероятноезначение
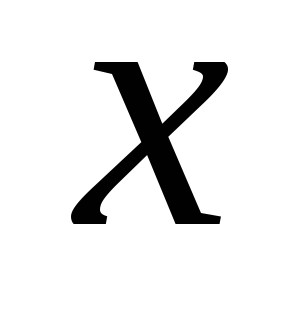 :
: ;
;о
 тклонения
тклонения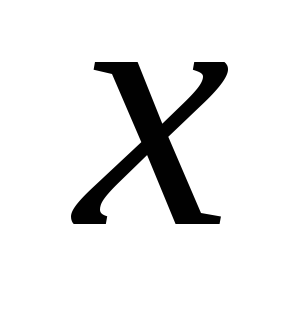 от
от в обе стороны встречаются одинаково
часто: гауссово распределение симметрично
относительно
в обе стороны встречаются одинаково
часто: гауссово распределение симметрично
относительно ,
поэтому среднее значение
,
поэтому среднее значение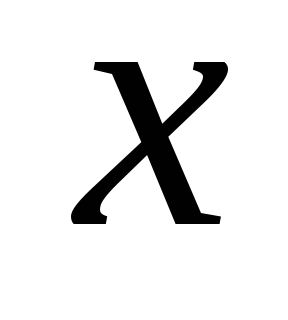 (обозначим его
(обозначим его ),
называемое такжематематическим
ожиданиемвеличины
),
называемое такжематематическим
ожиданиемвеличины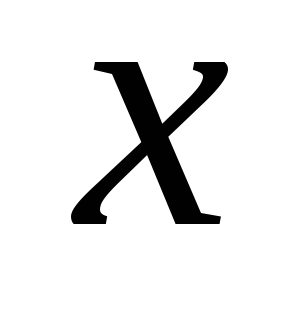 ,
равно
,
равно :
: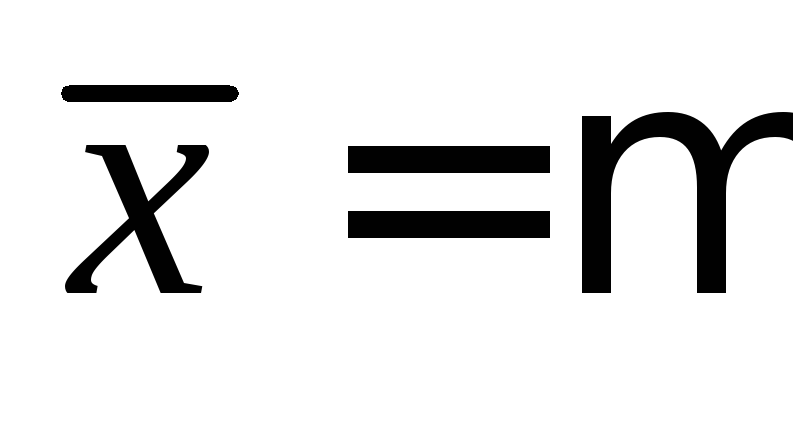 ;
;чем больше отклонение
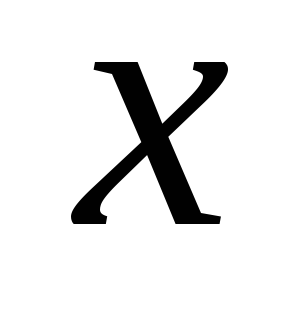 от
от ,
тем реже оно встречается;
,
тем реже оно встречается;мерой случайной погрешности, т. е. мерой отклонения
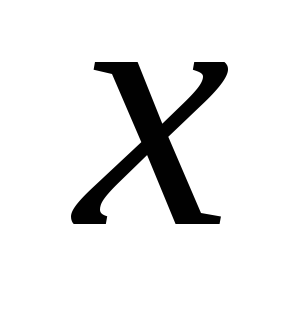 от
от ,
являетсястандартноеилисреднеквадратичноеотклонение
(СКО). Обозначим его буквой
,
являетсястандартноеилисреднеквадратичноеотклонение
(СКО). Обозначим его буквой .
Оно примерно равно полуширине на
полувысоте (ПШПВ) гауссова
распределения: ПШПВ
.
Оно примерно равно полуширине на
полувысоте (ПШПВ) гауссова
распределения: ПШПВ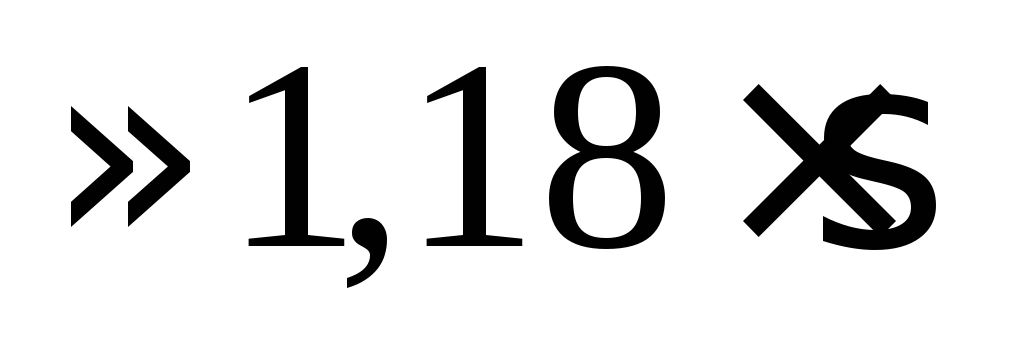 ;
;при
 всё распределение «стягивается» к
одному значению
всё распределение «стягивается» к
одному значению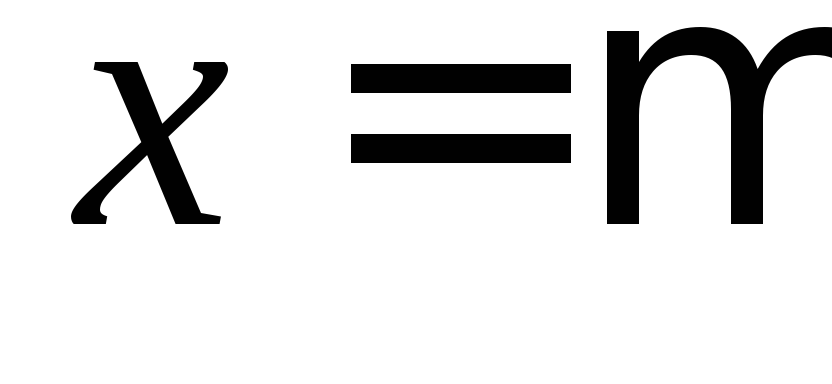 ,
которое в отсутствие систематической
погрешности и принимается за истинное
значение
,
которое в отсутствие систематической
погрешности и принимается за истинное
значение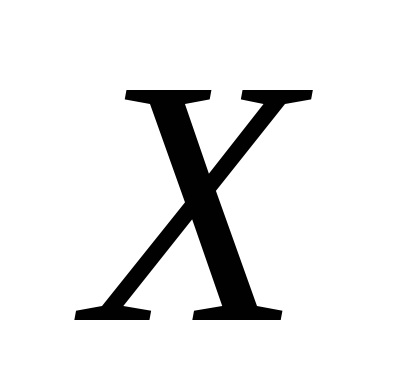 ;
;в интервал от
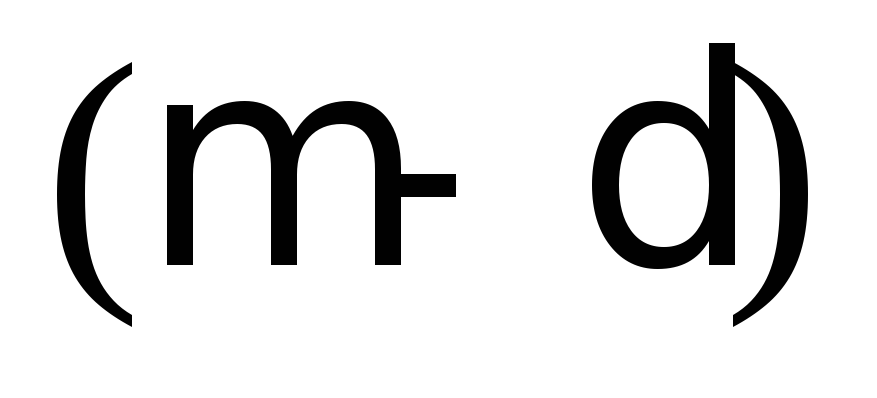 до
до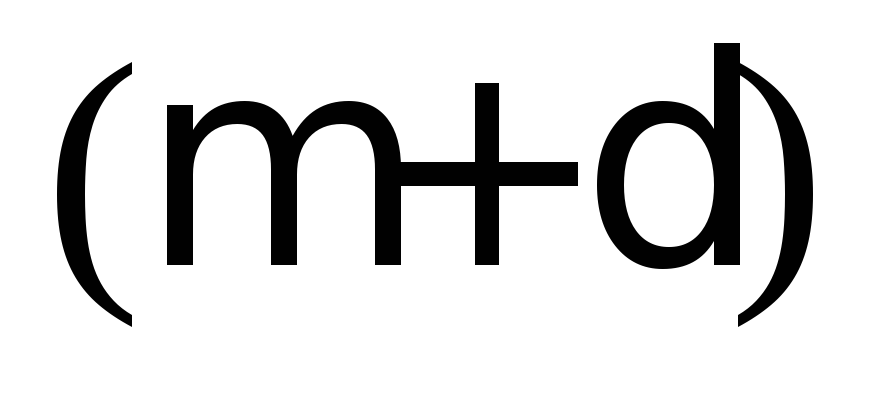 ,
т. е.
,
т. е. вокруг
вокруг попадает 68 % всех результатов
измерений, в интервал
попадает 68 % всех результатов
измерений, в интервал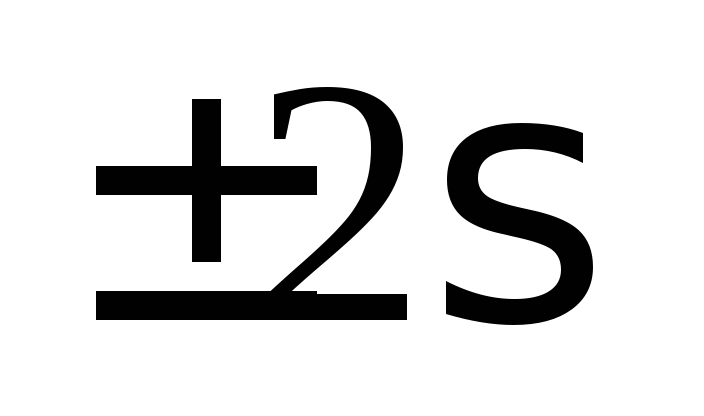 – 95 %,а в интервале
– 95 %,а в интервале заключено 99,73 % всех результатов. На
долю отклонений от
заключено 99,73 % всех результатов. На
долю отклонений от ,
превышающих
,
превышающих ,приходится всего
,приходится всего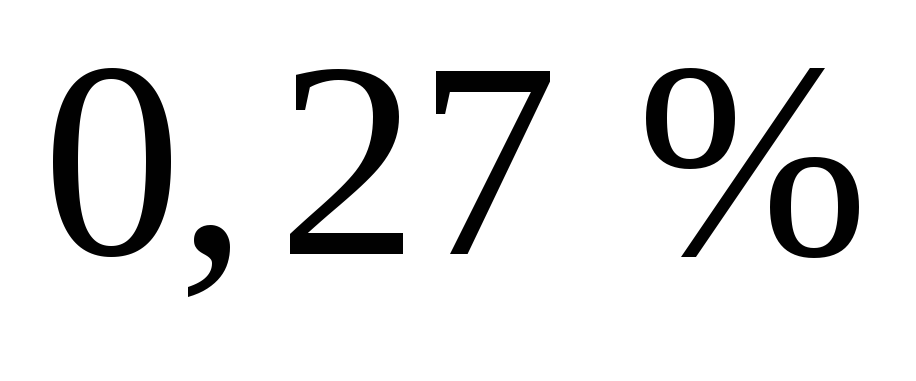 общего числа измерений. Все эти оценки
можно кратко записать в виде одной
формулы: с вероятностью
общего числа измерений. Все эти оценки
можно кратко записать в виде одной
формулы: с вероятностью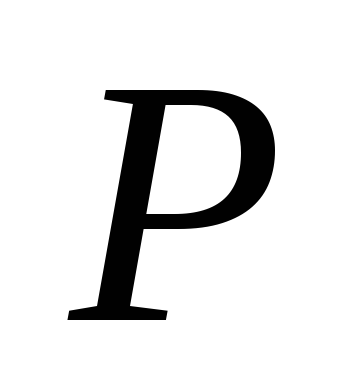 интервал между
интервал между и результатом любого измерения
и результатом любого измерения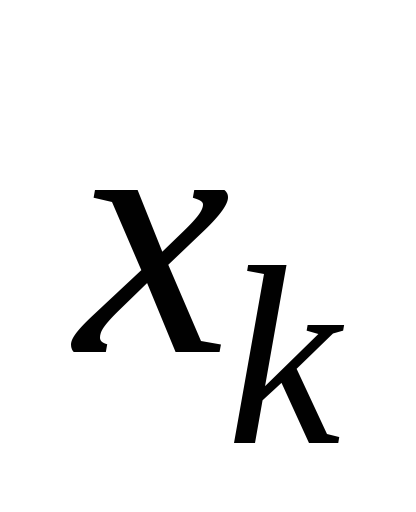 (т. е. фактически погрешность измерения
(т. е. фактически погрешность измерения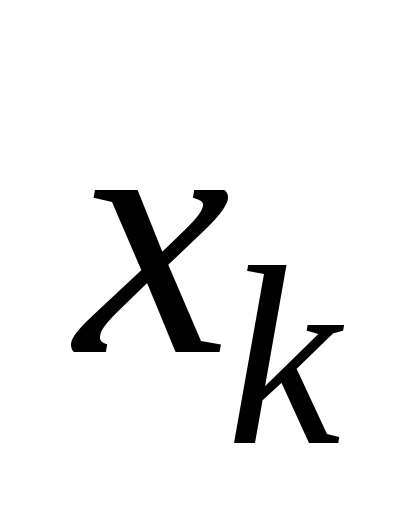 )
не превышает
)
не превышает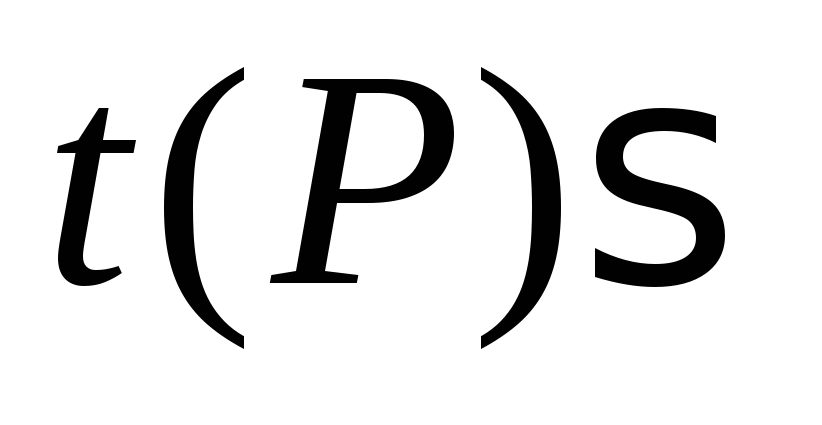 :
:
![]() .
(3)
.
(3)
При
![]()
![]() ,
т. е.
,
т. е.![]() ,
соответственно
,
соответственно![]() ,
,![]() .
.
Из
формулы (3) получаются варианты так
называемого доверительного интерваладля истинного значения![]() ,
т. е. интервала, в котором
,
т. е. интервала, в котором![]() находится с заданнойдоверительной
вероятностью
находится с заданнойдоверительной
вероятностью
![]() .
Запись
.
Запись
![]()
![]() (4)
(4)
означает,
что истинное значение
![]() находится в интервале от
находится в интервале от![]() до
до![]() (который называетсядоверительным
интервалом) с вероятностью
(который называетсядоверительным
интервалом) с вероятностью![]() (которая называетсядоверительной
вероятностью).
(которая называетсядоверительной
вероятностью).
Прямые измерения.При прямых измерениях физическая величина считывается непосредственно со шкалы прибора. С помощью микросекундомера в данной работе осуществляется прямое измерение интервала времени. Перед каждым измерением показание МС необходимо обнулить.
Если
истинное значение
![]() и СКО измеряемой величины неизвестны,
то их можно определить многократными,
т. е. повторяющимися в одной и той же
неизменной экспериментальной обстановке,
измерениями. Именно это мы проделаем
во вводном лабораторном занятии. При
многократных измерениях расчётной
оценкой математического ожидания
и СКО измеряемой величины неизвестны,
то их можно определить многократными,
т. е. повторяющимися в одной и той же
неизменной экспериментальной обстановке,
измерениями. Именно это мы проделаем
во вводном лабораторном занятии. При
многократных измерениях расчётной
оценкой математического ожидания![]() (т. е. истинного значения
(т. е. истинного значения![]() )
являетсявыборочное среднее
)
являетсявыборочное среднее![]() (т. е. среднее арифметическое результатов
серии из
(т. е. среднее арифметическое результатов
серии из![]() измерений, которую называютвыборкой):
измерений, которую называютвыборкой):
![]() .
(5)
.
(5)
Расчётной
оценкой СКО (![]() )
являетсявыборочное СКО(
)
являетсявыборочное СКО(![]() ):
):
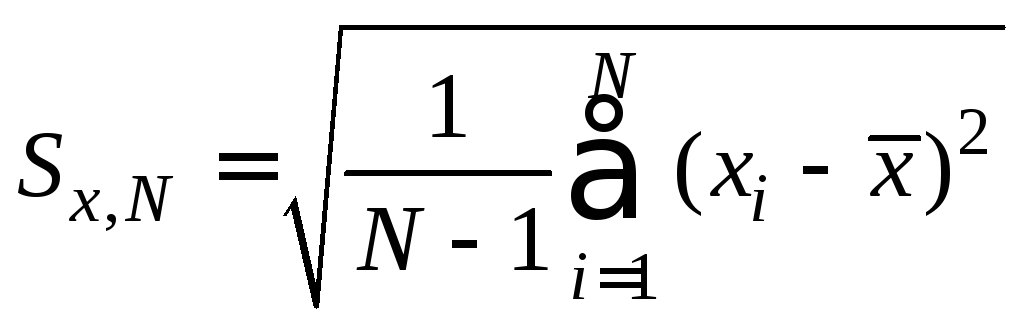 .
(6)
.
(6)
Многие из инженерных калькуляторов имеют режим статистических вычислений (STAT), существенно упрощающий вычисления по формулам (5), (6).
При
![]()
![]() ,
а
,
а![]() .
Поэтому, казалось бы, можно по аналогии
с (4) записать результат измерений в
виде:
.
Поэтому, казалось бы, можно по аналогии
с (4) записать результат измерений в
виде:
![]() ,
,
![]() .
.
Однако
при любом конечном числе измерений
выборочное СКО может оказаться как
больше, так и меньше неизвестного
![]() .
Второй случай – самый опасный: при
подстановке
.
Второй случай – самый опасный: при
подстановке![]() вместо
вместо![]() преуменьшается ширина доверительного
интервала. Заданную доверительную
вероятность обеспечивают, расширяя
интервал путём замены коэффициентов
преуменьшается ширина доверительного
интервала. Заданную доверительную
вероятность обеспечивают, расширяя
интервал путём замены коэффициентов![]() на коэффициенты Стьюдента
на коэффициенты Стьюдента![]() (табл. 3). При этом
(табл. 3). При этом![]() .
Из таблицы видно, что, например
.
Из таблицы видно, что, например![]()
![]() только при
только при![]() ,
т. е. только при таком числе измерений
,
т. е. только при таком числе измерений![]() незначительно отличается от
незначительно отличается от![]() .
.
Кроме
того, для сужения интервала, т. е. для
уточнения оценки
![]() ,
используют то, что выборочное
среднее
,
используют то, что выборочное
среднее![]() в (7) зависит от суммы случайных нормально
распределённых результатов измерений
в (7) зависит от суммы случайных нормально
распределённых результатов измерений![]() и потому само является случайной
нормально распределённой величиной со
среднеквадратичным отклонением среднего
и потому само является случайной
нормально распределённой величиной со
среднеквадратичным отклонением среднего![]() .
В математической статистике доказывается,
что если результаты измерений не зависят
друг от друга, то
.
В математической статистике доказывается,
что если результаты измерений не зависят
друг от друга, то
![]() .
.
|
Таблица 3 | |||||
|
N |
Р | ||||
|
0,683 |
0,900 |
0,950 |
0,990 |
0,997 | |
|
t(P, N) | |||||
|
2 |
1,84 |
6,3 |
12,7 |
63,6 |
212,3 |
|
3 |
1,32 |
2,9 |
4,3 |
9,9 |
182 |
|
4 |
1,20 |
2,4 |
3,2 |
5,8 |
9,0 |
|
5 |
1,14 |
2,1 |
2,8 |
4,6 |
6,4 |
|
6 |
1,11 |
2,0 |
2,6 |
4,0 |
5,4 |
|
7 |
1,09 |
1,9 |
2,4 |
3,7 |
4,8 |
|
8 |
1,08 |
1,9 |
2,4 |
3,5 |
4,4 |
|
9 |
1,07 |
1,9 |
2,3 |
3,4 |
4,2 |
|
10 |
1,06 |
1,8 |
2,3 |
3,2 |
4,0 |
|
15 |
1,04 |
1,8 |
2,1 |
3,0 |
3,6 |
|
20 |
1,03 |
1,7 |
2,1 |
2,9 |
3,4 |
|
30 |
1,02 |
1,7 |
2,0 |
2,8 |
3,2 |
|
50 |
1,01 |
1,7 |
2,0 |
2,7 |
3,1 |
Точное
значение
![]() неизвестно, однако при большом числе
измерений
неизвестно, однако при большом числе
измерений![]() ,
откуда
,
откуда
![]() .
.
Видно,
что погрешность приближения
![]() при больших
при больших![]() уменьшается как
уменьшается как![]() .
Это означает, что хотя от измерения к
измерению единичные результаты «прыгают»
в среднем на
.
Это означает, что хотя от измерения к
измерению единичные результаты «прыгают»
в среднем на![]() ,
разброс выборочных средних от выборки
к выборке по
,
разброс выборочных средних от выборки
к выборке по![]() случайных измерений уменьшается с
ростом
случайных измерений уменьшается с
ростом![]() ,
что и позволяет сузить доверительный
интервал при многократных измерениях.
Уменьшение случайного разброса путём
усреднения многократных измерений
широко используется в цифровых приборах.
,
что и позволяет сузить доверительный
интервал при многократных измерениях.
Уменьшение случайного разброса путём
усреднения многократных измерений
широко используется в цифровых приборах.
Используя коэффициенты Стьюдента и переходя к выборочному СКО среднего значения, окончательно запишем результат в случае многократных измерений
![]() ,
,
![]() .
(7)
.
(7)
Значения
![]() ,
отличные от 1, 2, 3, и соответствующие
значения
,
отличные от 1, 2, 3, и соответствующие
значения![]() могут быть выбраны по таблицам в [1,2,6].Рекомендуется результат записывать
для
могут быть выбраны по таблицам в [1,2,6].Рекомендуется результат записывать
для
![]() ,
т. е. выбирать доверительный интервал
,
т. е. выбирать доверительный интервал
![]() ,
так как при
,
так как при![]()
![]() при достаточно большом числе измерений.
Именно такое значение
при достаточно большом числе измерений.
Именно такое значение![]() выбирают
выбирают![]() по
умолчанию: если доверительная вероятность
в записи (7) не указана, то
по
умолчанию: если доверительная вероятность
в записи (7) не указана, то![]() ,
а доверительный интервал соответственно
есть промежуток от
,
а доверительный интервал соответственно
есть промежуток от![]() до
до
![]() .
.
