Тема 6. Изучение взаимосвязей по временным рядам

1. Метод отклонений от тренда

Пусть имеются два временных ряда x_t и у_t каждый из которых содержит трендовую компоненту Τ и случайную компоненту ε. Проведение аналитического выравнивания по каждому из этих рядов позволяет найти параметры соответствующих уравнений трендов и определить расчетные по тренду уровниисоответственно. Эти расчетные значения можно принять за оценку трендовой компоненты T каждого ряда. Поэтому влияние тенденции можно устранить путем вычитания расчетных значений уровней ряда из фактических. Эту процедуру проделывают для каждого временного ряда в модели. Дальнейший анализ взаимосвязи ря­дов проводят с использованием не исходных уровней, а отклоне­ний от трендаипри условии, что последние не со­держат тенденции.

Содержательная интерпретация параметров полученной модели за­труднительна, однако ее можно использовать для прогнозирова­ния. Для этого необходимо определить трендовое значение фак­торного признакаи с помощью одного из методов оценить ве­личину предполагаемого отклонения фактического значения от трендового. Далее по уравнению тренда для результативного при­знака определяют трендовое значение, а по уравнению регрес­сии по отклонениям от трендов находят величину отклонения . Затем находят точечный прогноз фактического значения y_t по формуле

2. Метод последовательных разностей

В ряде случаев вместо аналитического выравнивания времен­ного ряда с целью устранения тенденции можно применить более простой метод — метод последовательных разностей.

Если временной ряд содержит ярко выраженную линейную тенденцию, ее можно устранить путем замены исходных уровней ряда цепными абсолютными приростами (первыми разностями).

Если временной ряд содержит тенденцию в форме параболы второго порядка, то для ее устранения можно заменить исходные уровни ряда на вторые разности.

При всейсвоей простоте метод последовательных разностей имеет два су­щественных недостатка. Во-первых, его применение связано с со­кращением числа пар наблюдений, по которым строится уравне­ние регрессии, и, следовательно, с потерей числа степеней свобо­ды. Во-вторых, использование вместо исходных уровней времен­ных рядов их приростов или ускорений приводит к потере ин­формации, содержащейся в исходных данных.

3. Включение в модель регрессии фактора времени

В корреляционно-регрессионном анализе устранить воздей­ствие какого-либо фактора можно, если зафиксировать воздейст­вие этого фактора на результат и другие включенные в модель факторы. Этот прием широко используется в анализе временных рядов, когда тенденция фиксируется через включение фактора времени в модель в качестве независимой переменной.

Модель вида

относится к группе моделей, включающих фактор времени. Оче­видно, что число независимых переменных в такой модели может быть больше единицы. Кроме того, это могут быть не только те­кущие, но и лаговые значения независимой переменной, а также лаговые значения результативной переменной.

Преимущество данной модели по сравнению с методами от­клонений от трендов и последовательных разностей в том, что она позволяет учесть всю информацию, содержащуюся в исход­ных данных, поскольку значения y_t и x_t есть уровни исходных временных рядов. Кроме того, модель строится по всей совокуп­ности данных за рассматриваемый период в отличие от метода последовательных разностей, который приводит к потере числа наблюдений. Параметры а и b модели с включением фактора вре­мени определяются обычным МНК. Расчет и интерпретацию па­раметров покажем на примере.

Автокорреляция в остатках.

Рассматривая последовательность остатков как временной ряд, можно построить график их зависимости от времени. В со­ответствии с предпосылками МНК остатки ε_t должны быть слу­чайными (рис. 1 а). Однако при моделировании временных ря­дов нередко встречается ситуация, когда остатки содержат тен­денцию (рис. 1 б) и в)) или циклические колебания (рис.1 г)). Это свидетельствует о том, что каждое следующее значение ос­татков зависит от предшествующих. В этом случае говорят о на­личии автокорреляции остатков.

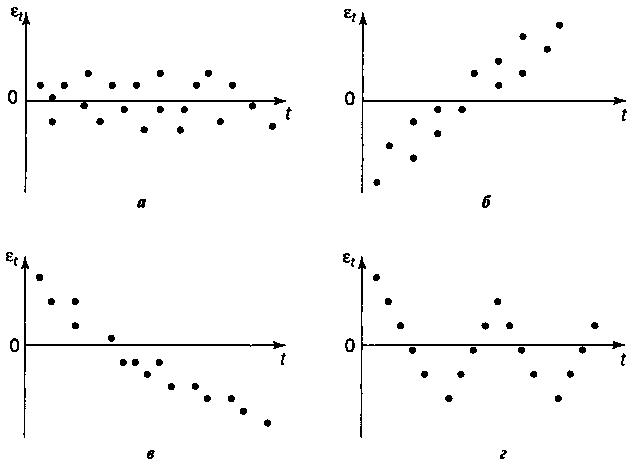
Рис. 1. Модели зависимости остатков от времени

а— случайные остатки; б — возрастающая тенденция в остатках;

в - убывающая тенденция в остатках;

г - циклические колебания в остатках

Существуют два наиболее распространенных метода опреде­ления автокорреляции остатков. Первый метод - это построение графика зависимости остатков от времени и визуальное определение наличия или отсутствия автокорреляции. Второй метод — использо­вание критерия Дарбина — Уотсона и расчет величины

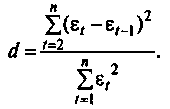
Соотношение между критерием Дарбина — Уотсона и коэф­фициентом автокорреляции остатков первого порядка:

Таким образом, если в остатках существует полная положи­тельная автокорреляция и= 1, тоd = 0. Если в остатках полная отрицательная автокорреляция, то= -1 и, следовательно,d = 4. Если автокорреляция остатков отсутствует, то= 0 иd = 2. Следовательно,

0 ≤ d ≤ 4.

Алгоритм выявления автокорреляции остатков на основе критерия Дарбина - Уотсона следующий. Выдвигается гипотеза H₀ об отсутствии автокорреляции остатков. Альтернативные ги­потезы Н₁ и H*₁ состоят, соответственно, в наличии положитель­ной или отрицательной автокорреляции в остатках. Далее по спе­циальным таблицам (см. приложение) определяются критичес­кие значения критерия Дарбина - Уотсона d_L и d_U для заданного числа наблюдений n, числа независимых переменных модели k и уровня значимости α. По этим значениям числовой промежуток [0;4] разбивают на пять отрезков. Принятие или отклонение каж­дой из гипотез с вероятностью (1 — α) рассматривается на рис. 2.

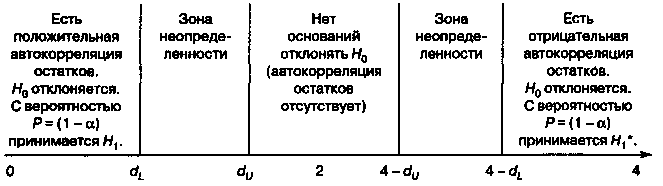
Рис. 2. Механизм проверки гипотезы о наличии автокорреляции остатков

Если фактическое значение критерия Дарбина — Уотсона по­падает в зону неопределенности, то на практике предполагают существование автокорреляции остатков и отклоняют гипотезу H₀.

Есть несколько существенных ограничений на применение критерия Дарбина — Уотсона.

Во-первых, он неприменим к моделям, включающим в качест­ве независимых переменных лаговые значения результативного признака, т. е. к моделям авторегрессии. Для тестирования на ав­токорреляцию остатков моделей авторегрессии используется критерий h Дарбина.

Во-вторых, методика расчета и использования критерия Дар­бина — Уотсона направлена только на выявление автокорреляции остатков первого порядка. При проверке остатков на автокорре­ляцию более высоких порядков следует применять другие методы, рассмотрение которых выходит за рамки данного учебника.

В-третьих, критерий Дарбина — Уотсона дает достоверные результаты только для больших выборок. В этом смысле резуль­таты примера 6.4 нельзя считать достоверными ввиду чрезвычай­но малого числа наблюдений n = 7, по которым построена модель регрессии.