Трудоемкость решения задачи на основе рассматриваемого алгоритма, по крайней мере, для рассмотренного примера достаточно велика. Впрочем, практика его применения показывает, что большинство задач характеризуется существенно меньшей трудоемкостью.

5.3. Примеры решения стратегических матричных игр

Рассмотренные ниже примеры позволяют сделать некоторые выводы в плане сравнительного анализа возможностей рассмотренных методов решения стратегических матричных игр, а также практического значения получаемых решений.

Пример 42. В игре, матрица которой представлена в табл. 48,

нижняя цена α=2, верхняя β=4, седловая точка отсутствует. Решим данную игру тремя рассмотренными выше методами.

Таблица 48

Метод упрощения. Исключим последовательно заведомо невыгодные стратегии: А4 по сравнению с А1, В3 по сравнению с В2 (без учета уже исключенной четвертой строки матрицы), А2 по сравнению с А3 (без учета уже исключенного третьего столбца матрицы). Матрица игры после выполненных упрощений представлена в табл. 49.

Таблица 49

149

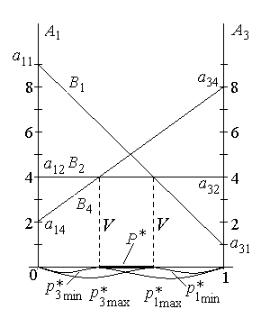
Решение можно продолжить графическим способом (рис. 40). Особенностью рассматриваемой игры является наличие бесконечного множества решений, включающего в себя:

а) смешанную стратегию, соответствующую левому концу отрезка, показанного на рис. 40 жирной линией (оптимальные частоты применения чистых стратегий для стороны А отмечены на

рисунке как p1*max и p3*min , для стороны В полезны стратегии В2 и

В4);

б) смешанную стратегию, соответствующую правому концу отрезка, показанного на рис. 40 жирной линией (оптимальные частоты применения чистых стратегий для стороны А отмечены

на рисунке как p1*min и p3*max , для стороны В полезными являются стратегии В1 и В2);

в) для стороны А любую смешанную стратегию с частотами

p1*min < p1 < p1*max , p3*min < p3 < p3*max , p1 +p3 =1 (множество точек

отрезка, показанного на рис. 40 жирной линией), для стороны В – чистую стратегию В2.

Рис. 40

150

Учитывая в каждом случае только полезные стратегии, получаем аналогично рассмотренным выше примерам численное решение:

– для варианта а)

– для варианта б)

В общем виде результат, полученный методом упрощения, можно сформулировать следующим образом: для стороны А оптимальна любая смешанная стратегия с частотами

0,375 ≤ p1 ≤ 0,67 , p3 =1–p1 , для стороны В – чистая стратегия В2.

Метод линейного программирования. Отметим сразу, что при использовании данного метода предварительное исключение заведомо невыгодных стратегий позволяет значительно снизить размерность задачи и соответственно трудоемкость решения. Воспользуемся этим и перейдем к задаче линейного программирования для упрощенной игры (табл. 49). Решение получаемой задачи линейного программирования симплекс-методом представлено в табл. 50...52.

Таблица 50

151

стратегии), оптимальные частоты применения стратегий стороны В q1* = x3V = 0 , q2* = x4V =1/ 4 4 =1, q3* = 0 (заведомо невыгодная), q4* = x5V = 0 (соответствует свободной переменной двойст-

венной задачи линейного программирования).

Таким образом, симплекс-метод дает возможность найти лишь одно частное решение из бесконечного множества решений, имеющихся в рассматриваемой задаче. Нетрудно убедиться, что графический метод, рассмотренный в подразд. 4.1, позволяет получить здесь все множество решений. Любой же формальный метод решения задачи линейного программирования дает эффект, аналогичный симплекс-методу.

Численное решение рассмотренной задачи с помощью итерационнго алгоритма Брауна-Робинсон приводит к следующим ре-

152

зультатам: после 105 партий игры опытная стратегия стороны А p1=0,6658; p2=0; p3=0,3342; p4=0; стороны В q1=0,0004; q2=0,9980; q3=0; q4=0,0016; средний выигрыш стороны А (оценка величины цены игры) V=4,0005.

Нетрудно видеть, что алгорим Брауна-Робинсон аналогично симплекс-методу также приводит к одному из возможных частных решений задачи.

Теперь рассмотрим практический пример, требующий предварительной формализации (пример 8 из разд. 1).

Пример 8 (продолжение). Примем, что имеются четыре группы покупателей, выбор из которых конкретной группы любой из сторон равновероятен. Перечислим все возможные чистые стратегии сторон.

Для стороны (фирмы) А

A1: 1+1+0+0 (имеющиеся партии продукции предлагаются двум разным группам покупателей);

A2: 2+0+0+0 (обе партии продукции предлагаются одной группе покупателей).

Для стороны (фирмы) В

B1: 1+1+1+1 (партии продукции предлагаются четырем разным группам покупателей);

B2: 2+2+0+0 (двум разным группам покупателей предлагаются по две партии продукции);

B3: 2+1+1+0 (одной произвольно выбранной группе покупателей предлагаются две партии продукции, двум по одной партии);

B4: 3+1+0+0;

B5: 4+0+0+0.

С учетом сформулированных в разд. 1 условий задачи рассчитаем величины вероятности заключения стороной А контракта на реализацию хотя бы одной партии продукции для всех возможных сочетаний стратегий сторон и составим матрицу игры (табл. 53).

Таблица 53

153