
- •ВВЕДЕНИЕ
- •ШАГ 1. МЕТОД ПРОЕКЦИЙ. ТОЧКА
- •1.1. Метод проекций
- •1.2. Система координат и плоскостей проекций
- •1.3. Проецирование точки на плоскости проекций
- •1.4. Точка на комплексном чертеже
- •Итоги первого шага
- •ШАГ 2. ПРЯМАЯ
- •2.1. Прямые частного положения
- •2.2. Следы прямой
- •2.4. Построение проекций отрезка заданной длины
- •2.5. Относительное положение прямых
- •2.6. Теорема о частном случае проецирования прямого угла
- •Итоги второго шага
- •ШАГ 3. ПЛОСКОСТЬ. ТОЧКА И ЛИНИИ В ПЛОСКОСТИ
- •3.1. Задание плоскости на чертеже. Точка в плоскости
- •3.2. Следы плоскости
- •3.3. Горизонталь и фронталь плоскости
- •3.4. Линии наибольшего наклона плоскости к плоскостям проекций
- •Итоги третьего шага
- •ШАГ 4. ПЛОСКОСТИ ОБЩЕГО И ЧАСТНОГО ПОЛОЖЕНИЯ
- •4.1. Проецирующая плоскость
- •4.1.1. Свойство собирательности проецирующей плоскости
- •4.1.2. О некоторых способах задания проецирующей плоскости на чертеже
- •4.1.3. Точка встречи прямой с проецирующей плоскостью
- •4.1.4. Линия пересечения двух плоскостей, одна из которых проецирующая
- •4.2. Плоскости уровня
- •Итоги четвёртого шага
- •ШАГ 5. ОТНОСИТЕЛЬНОЕ ПОЛОЖЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ ОБЩЕГО ПОЛОЖЕНИЯ
- •5.1. Точка встречи прямой с плоскостью общего положения
- •5.2. Определение видимости прямой относительно плоскости
- •5.3. Прямая, перпендикулярная плоскости
- •5.4. Прямая, параллельная плоскости
- •Итоги пятого шага
- •ШАГ 6. ОТНОСИТЕЛЬНОЕ ПОЛОЖЕНИЕ ПЛОСКОСТЕЙ
- •6.1. Пересечение двух плоскостей
- •6.2. Взаимно перпендикулярные плоскости
- •6.3. Параллельные плоскости
- •Итоги шестого шага
- •ПОМОЩЬ НА ОСТАНОВКАХ
- •ЗАКЛЮЧЕНИЕ
|
|
f0a |
|
A" |
|
x |
|
2" 1' |
|
|
|
h0a |
A' |
2' |
|
1" |
|
|
|
|
|
|
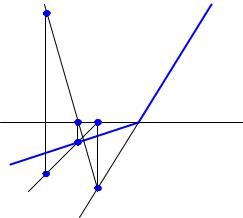
Рис. 3.15 |
3.3. Горизонталь и фронталь плоскости |
||
Рассматривая прямые частного положения, мы уже познакомились с прямыми уровня: горизонталью, фронталью и профилью. Теперь рассмотрим горизонталь и фронталь плоскости. Горизонталь плоскости – это прямая, принадлежащая плоскости и параллельная горизонтальной плоскости проекций. Следовательно, у всех точек горизонтали координата z постоянна. Поэтому ее фронтальная проекция ( h′′) параллельна оси X (рис. 3.16). Можно сказать, что горизонтальный след плоскости h0α – это тоже горизонталь, только координата z=0. А все горизонтали одной
плоскости параллельны друг другу. Мы знаем, что у параллельных прямых одноименные проекции параллельны. Следовательно, горизонтальная проекция горизонтали параллельна горизонтальному следу плоскости (т.е. h′// h0α ).
Обратите внимание, что горизонталь обозначается h, а горизонтальный след – h0 . Говорят,
что горизонтальный след – это нулевая горизонталь.
Фронталь плоскости – это прямая, принадлежащая плоскости и параллельная фронтальной плоскости проекций (рис. 3.17). У фронтали плоскости горизонтальная проекция параллельна оси X, а фронтальная параллельна фронтальному следу, так как у всех точек фронтали координата y постоянна. У фронтального следа y=0, поэтому фронтальный след – это нулевая фронталь.
Напомним, что горизонтали и фронтали плоскости (так же как и любые прямые) предполагаются бесконечными.
Профиль плоскости – это прямая, принадлежащая плоскости и параллельная профильной плоскости проекций.
Для решения рассмотренной ранее задачи построения недостающей проекции точки, принадлежащей плоскости, в ряде случаев удобнее в качестве вспомогательной прямой взять горизонталь или фронталь плоскости.
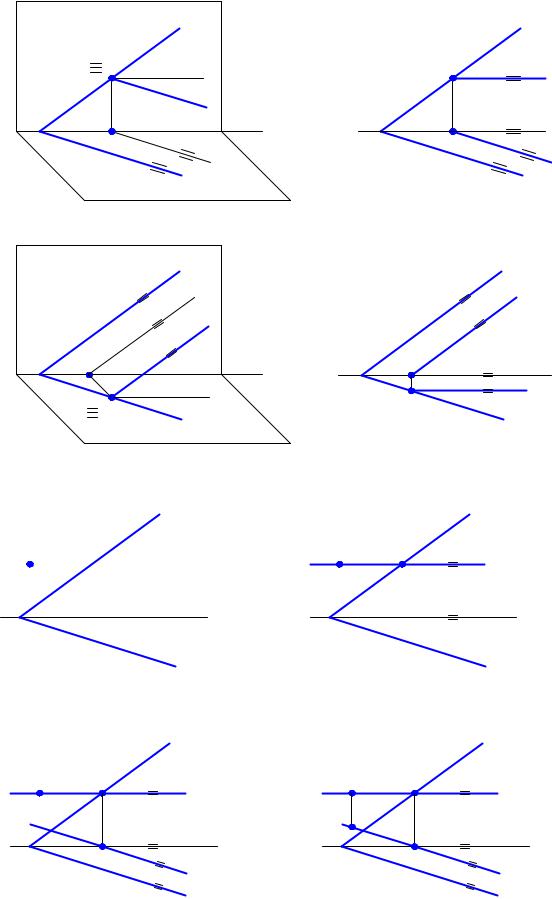
Исходные данные задачи представлены на рис. 3.18,а. Проведем через фронтальную проекцию горизонтали ( h′′//оси X) (рис. 3.18,б). Горизонталь пересекается с фронтальным следом в точ-
ке 1 |
′′ |
– пересечение |
f0α и h |
′′ |
). Построив горизонтальную проекцию точки 1, через нее можно |
(1 |
|
провести горизонтальную проекцию горизонтали параллельно горизонтальному следу (рис. 3.18,в). С помощью линии проекционной связи строится горизонтальная проекция точки A, лежащая на горизонтали h (рис. 3.18,г). Задача решена.
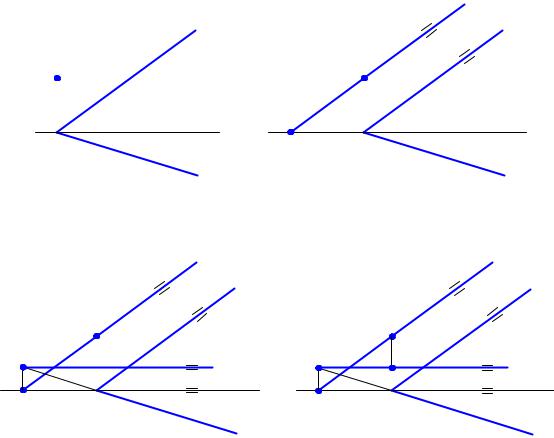
Возьмем те же самые исходные данные (рис. 3.19,а). Только теперь для построения недостающей проекции точки в качестве вспомогательной прямой используем фронталь плоскости. Через A′′ проведем f ′′ – фронтальную проекцию фронтали (она проходит параллельно фронталь-
ному следу). Там, где она пересечет ось X, будет находиться фронтальная проекция точки 1 (рис. 3.19,б). Поскольку у точки 1 z=0, она принадлежит горизонтальному следу. Продлив h0α , можно построить горизонтальную проекцию точки 1, лежащей на фронтали (рис. 3.19,в), и провести через нее горизонтальную проекцию фронтали ( f ′// X ). На рис. 3.19,г приведено окончательное решение задачи.
36
|
|
|
f0a |
|
1 |
1" |
h" |
|
|
1' |
h |
x |
|
|
|
|
|
h' |
|
|
|
|
|
|
|
|
h0a |
|
|
|
a |
|
|
|
f0a |
|
|
|
f" |
|
2" |
|
f |
x |
|
f' |
|
|
|
||
|
|
|
|
|
2 |
2' |
h0a |
|
|
|
|
|
|
|
a |
|
|
|
f0a |
|
A" |
|
|
x |
|
|
|
|
|
a |
h0a |
|
|
|
|
|
|
|
f0a |
|
A" |
1" |
h" |
|
|
||
x |
|
1' |
h' |
|
|
|
h0a
â
|
|
f0a |
|
1" |
h" |
x |
1' |
|
h' h0a
Рис. 3.16 |
|
|
á |
|
|
|
|
|
|
|
f0a |
|
|
|
f" |
x |
|
2" |
f' |
|
|
||
|
|
|
|
|
|
2' |
h0a |
|
|
|
|
Рис. 3.17 |
|
|
á |
|
|
|
|
|
|
|
f0a |
|
A" |
1" |
h" |
|
|
x
|
|
á |
h0a |
|
|
|
|
|
|
|
f0a |
|
A" |
1" |
h" |
|
|
||
x |
A' |
1' |
|
|
h' |
||
|
|
|
|
|
|
|
h0a |
Рис. 3.18 |
|
ã |
|
37 |
|
|
|
|
f0a |
|
|
f" |
|
|
|
f0a |
|
|
A" |
|
A" |
|
x |
x |
1" |
|
|
|
h0a |
|
|
h0a |
|
a |
|
á |
|
|
f" |
|
|
f" |
|
f0a |
|
|
f0a |
1" |
A" |
|
A" |
|
f' |
1" |
A' |
f' |
|
x |
|
x |
|
|
1" |
|
1" |
|
|
|
h0a |
|
ã |
h0a |
|
â |
|
|
|
|
Рис. 3.19 |
|
|
|
3.4.Линии наибольшего наклона плоскости к плоскостям проекций
Вобщем случае плоскость образует с горизонтальной и фронтальной плоскостями проекций некоторые двугранные углы. Мерой двугранных углов служат линейные углы ( ϕ1 и ϕ2 ), полу-
чающиеся в сечении, перпендикулярном линии пересечения данной плоскости и соответствующей плоскости проекций (рис. 3.20,а и б).
Плоскость указанного сечения пересекается с заданной плоскостью по линии, называемой линией наибольшего наклона плоскости к соответствующей плоскости проекций. Линия наибольшего наклона принадлежит заданной плоскости и перпендикулярна соответствующему следу плоскости.
Линия наибольшего наклона плоскости к горизонтальной плоскости проекций называется линией ската. Она принадлежит заданной плоскости и перпендикулярна горизонтальному следу этой плоскости (или любой ее горизонтали, так как любая горизонталь плоскости параллельна горизонтальному следу).
Итак, нам необходимо провести в плоскости прямую, перпендикулярную горизонтали этой плоскости. Выясним, будет ли в этом случае справедлива теорема о частном случае проецирования прямого угла.
Поскольку одна из сторон прямого угла (в нашем случае горизонталь плоскости или горизонтальный след) параллельна горизонтальной плоскости проекций, то прямой угол на горизонтальную плоскость проекций будет проецироваться в истинную величину. Из этого следует, что горизонтальная проекция линии ската s перпендикулярна горизонтальному следу плоскости ( s′ h0α ,
рис. 3.21,а). Фронтальную проекцию линии ската определим из условия принадлежности ее плоскости α . Возьмем точки 1 и 2, принадлежащие как линии ската, так и следам плоскости, и построим фронтальную проекцию линии ската (рис. 3.21,б). На рис. 3.21,в показано, как определить
38
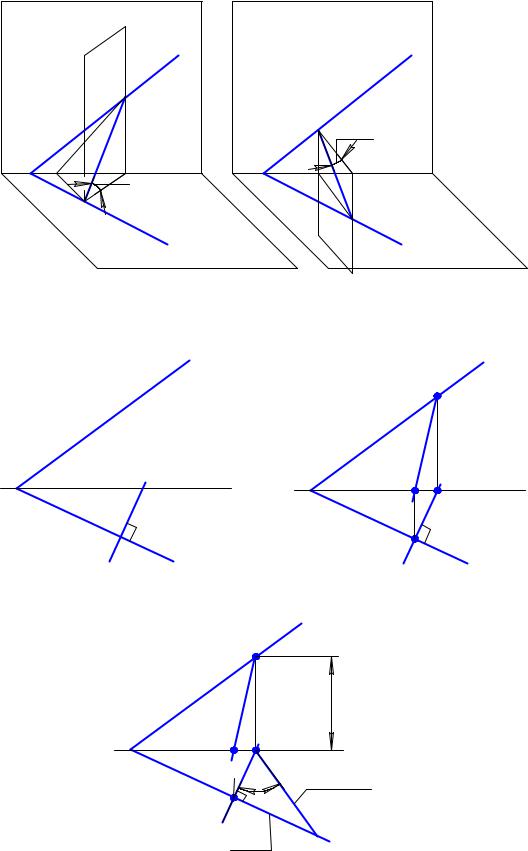
угол ϕ1 – угол наклона прямой s к горизонтальной плоскости проекций, а следовательно, угол наклона плоскости α к горизонтальной плоскости проекций.
b1 f0a
j1
h0a
à
Рис. 3.20
f0a
x
s'
h0a
a
|
|
1" |
|
s" |
|
x |
2" |
1' |
|
|
s'f1 |
|
2' |
|
Dz
â
f0a
f2
b2 |
h0a |
|
|
|
á |
f0a
1"
s"
x |
2" |
1' |
s'
2' h0a
á
f0a
Dz
è.â.12
h0a
39
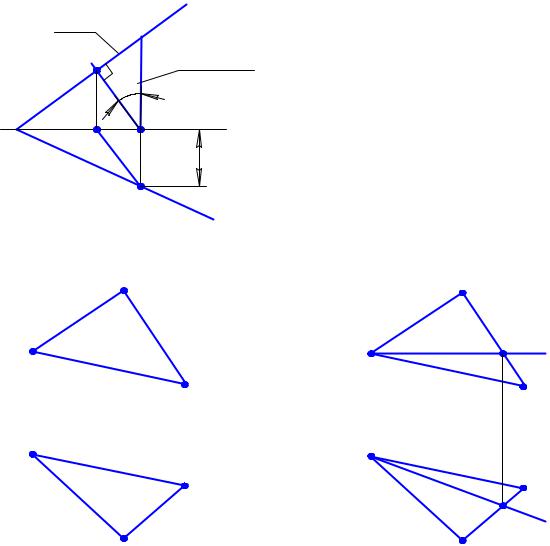
Рис. 3.21
Dy f0a
|
3" |
f |
|
è.â.3-4 |
|
|
|
||
|
|
|
|
|
|
|
2 |
|
|
x |
3' |
|
4" |
|
|
|
|
4' |
Dy |
|
|
|
|
|
|
|
Рис. 3.22 |
|
h0a |
|
|
B" |
|
|
A"
C"
A'
C'
B'
a
Рис. 3.22 иллюстрирует определение угла наклона плоскости к фронтальной плоскости проекций. Здесь отрезок 3 – 4 – линия наибольшего наклона к фронтальной плоскости проекций. Эта линия перпендикулярна фронтальному следу, следовательно (по теореме о частном случае проецирования прямого угла), ее фронтальная проекция перпендикулярна фронтальному следу. Угол ϕ2 – угол наклона прямой 3 – 4 к фронтальной
плоскости проекций.
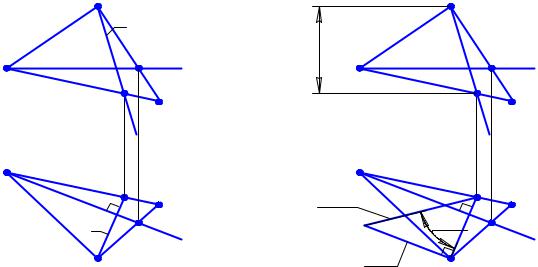
Рассмотрим аналогичную задачу при условии, что плоскость задана плоской фигурой (рис. 3.23,а). Обратите внимание, что в данном случае чертеж безосный, поэтому проще использовать не следы плоскости, а соответствующие линии уровня.
B"
1" h"
A"
C"
A'
C' 1' h'
B'
á
40
B"
s"
1" h"
A"
2" C"
A'
2'
C'
s'
1' h'
B'
â
Dz
Рис. 3.23
|
|
B" |
|
A" |
|
1" |
h" |
|
|
|
|
|
|
2" |
C" |
A' |
|
2' |
|
è.â. |
|
|
|
|
f1 |
C' |
|
|
|
||
|
Dz |
1' |
h' |
|
|
B'
ã
Прежде всего для нахождения угла наклона плоскости к горизонтальной плоскости проекций следует построить горизонталь этой плоскости. Начинаем построение с фронтальной проекции горизонтали. Эта проекция параллельна оси X (хотя на чертеже эта ось отсутствует, но ее направление мы знаем). Через точку A проведем h′′ и получим фронтальную проекцию вспомогательной точки 1 на пересечении В′′С′′ и h′′. Эта точка принадлежит прямой BC, лежащей в плоскости, следовательно, 1′ будет на B′C′. Поскольку горизонталь проведена через точку A, соединим A′ и 1′ и получим горизонтальную проекцию горизонтали h′. Горизонталь построена.
Теперь необходимо построить проекции линии ската s. Проведем ее через точку B (рис. 3.23,б). Мы уже знаем, что горизонтальная проекция линии ската перпендикулярна горизонтальной проек-
ции горизонтали, т.е. |
s |
′ |
′ |
s |
′ |
и на пересечении ее со стороной |
′ |
′ |
получим гори- |
|
h . Проведем |
|
A C |
|
|||||
зонтальную проекцию |
вспомогательной точки 2. Она нам нужна для построения фронтальной про- |
||||||||
екции линии ската. Проведя линию проекционной связи, получим фронтальную проекцию точки 2, а соединив фронтальные проекции точек B и 2, определим фронтальную проекцию линии ската. Проекции линии ската готовы. Осталось лишь определить угол наклона линии ската s к горизонтальной плоскости проекций. Это построение иллюстрирует рис. 3.23,г. Задача решена.
На рис. 3.24 приведено решение задачи на определение угла наклона плоскости к фронтальной плоскости проекций. Здесь через точку C проведена фронталь плоскости α( ABC) с помощью
вспомогательной точки 3, лежащей на стороне AB. Затем построена линия наибольшего наклона плоскости α к фронтальной плоскости проекций (это линия B-4, перпендикулярная фронтали). В
заключение определен угол ϕ2 – угол наклона плоскости к фронтальной плоскости проекций.
41
