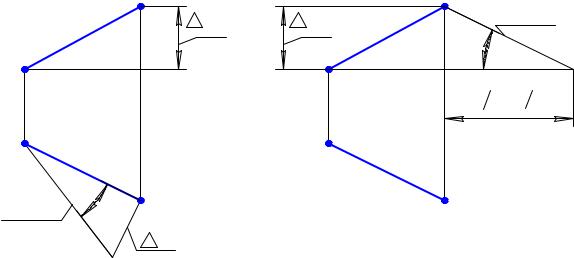
2.4. Построение проекций отрезка заданной длины

Рассмотрим задачу, исходные данные для которой приведены на рис. 2.18,а. Необходимо построить проекции отрезка AB, лежащего на прямой линии общего положения. Истинная величина отрезка задана.

При решении задач, связанных с истинной величиной отрезка, прежде всего надо проанализировать рассмотренные ранее варианты ее определения. Один из них приведен на рис. 2.18,б. Здесь четыре параметра: величина горизонтальной проекции, z , угол наклона отрезка к горизонтальной плоскости проекций ϕ1 и истинная величина отрезка. Какие из этих параметров мы можем

определить по исходным данным к задаче? Что нам известно, а что нет?

Итак, величина горизонтальной проекции отрезка неизвестна, z неизвестно, истинная величина отрезка известна. А угол наклона? Напрямую нет, но его легко можно определить, так как он от длины отрезка не зависит. С определения этого угла мы и начнем решение задачи. Возьмем на прямой произвольную точку 1 (рис. 2.18,в) и, построив истинную величину отрезка A1, определим угол ϕ1 .

Поскольку этот угол постоянен для всех отрезков данной прямой, истинная величина любого отрезка, начинающегося от точки A, будет лежать на линии A'10, в том числе и истинная величина отрезка AB. Отложим на этой прямой известную нам истинную величину отрезка AB (рис. 2.18,г) и построим горизонтальную проекцию точки B. Проведя линию проекционной связи, легко можно построить и фронтальную проекцию точки B. Задача решена.

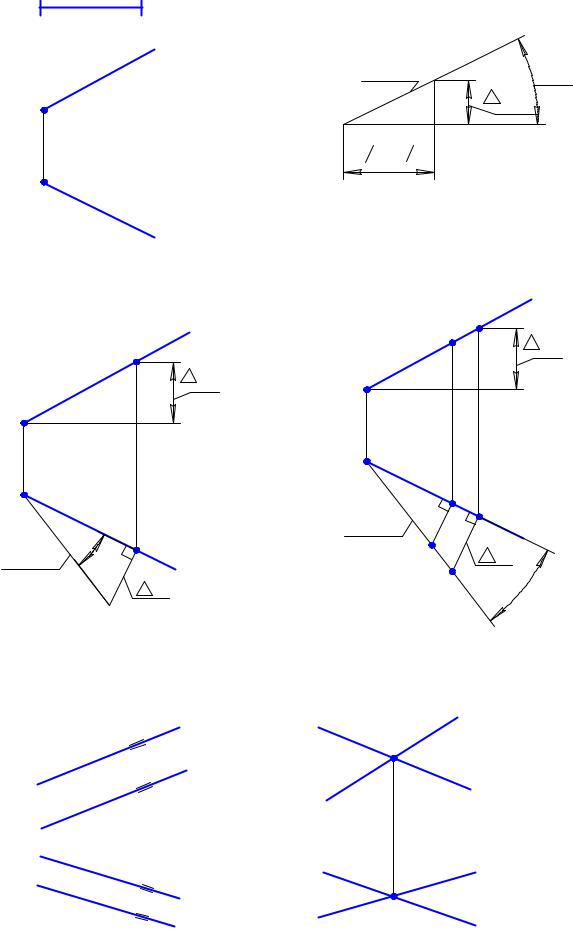
2.5. Относительное положение прямых

Две прямые могут быть по-разному расположены относительно друг друга:

•параллельные прямые (одноименные проекции параллельны) – рис. 2.19;

•пересекающиеся прямые (имеется одна общая точка, следовательно, точки пересечения одноименных проекций находятся в проекционной связи) – рис. 2.20;

•скрещивающиеся прямые (общих точек нет) – рис. 2.21.

23

24

n'

1'

3' 4' 2'

m'

Рис. 2.21

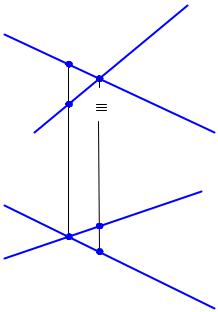
2.6.Теорема о частном случае проецирования прямого угла

Вобщем случае углы между прямыми линиями на плоскость проекций в натуральную величину не проецируются. Если мы возьмем прямоугольный треугольник, произвольно расположенный в пространстве, то на плоскость проекций он спроецируется в треугольник, у которого стороны и углы не спроецируются в натуральную величину.

Когда все углы треугольника спроецируются в натуральную величину? Тогда, когда плоскость треугольника будет параллельна плоскости проекций.

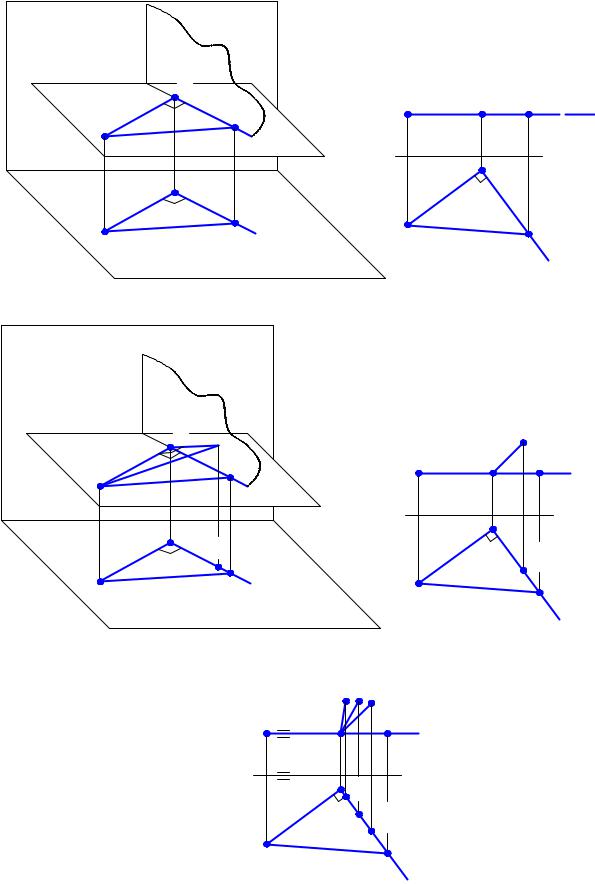
Пусть прямоугольный треугольник ABC расположен в плоскости, параллельной горизонтальной плоскости проекций (рис. 2.22,а,б). Проведем через катет BC плоскость, перпендикулярную горизонтальной плоскости проекций. Тогда горизонтальная проекция катета BC (т.е. B'C') будет

лежать на прямой l, являющейся линией пересечения плоскостей α и γ . Катет AB параллелен π1 и перпендикулярен плоскости γ . Горизонтальная проекция этого катета перпендикулярна плос-

кости и прямой l. Все углы треугольника ABC, в том числе и прямой угол, проецируются в истинную величину.

А теперь будем поворачивать треугольник ABC вокруг катета AB(рис. 2.22,в и г). При этом катет AB и его проекция A'B' своего положения не изменят; будет перемещаться лишь одна из вершин треугольника – точка C, занимая последовательно положения C, C1, C2, C3 (рис. 2.22,д).

Изменится ли при этом горизонтальная проекция катета BC? По величине – да, а по направлению – нет! Горизонтальная проекция катета BC будет при этом лежать на прямой l. А так как l′ A'B', то прямой угол при всех положениях треугольника (кроме случая, когда A займет положение A' и горизонтальная проекция треугольника превратится в отрезок прямой) будет проецироваться в натуральную величину. Таким образом, можно утверждать следующее.

Если одна из сторон прямого угла параллельна какой-либо плоскости проекций, а другая сторона не перпендикулярна, то прямой угол проецируется на эту плоскость проекций в натуральную величину. Это и есть теорема о частном случае проецирования прямого угла.

Рассмотрим еще один пример ( рис. 2.23,а).

Здесь прямые a и b взаимно перпендикулярны, так как прямая параллельна горизонтальной плоскости проекций, а горизонтальные проекции прямых a' и b' пересекаются под прямым углом, что соответствует условиям рассмотренной выше теоремы. Остается лишь проверить, а не перпендикулярна ли прямая b горизонтальной плоскости проекций. Если бы это было так, то прямая b на горизонтальную плоскость проекций спроецировалась бы в точку, чего не наблюдается в рассмотренном примере.

25

Вы уже, наверное, обратили внимание на то, что на чертеже нет фронтальной проекции прямой b (т.е. b"). Как же должна проходить эта проекция? Ясно, что через точку 1" , так как прямые a и b пересекающиеся, и ни в коем случае не перпендикулярно оси X, а в остальном – как угодно. Условие перпендикулярности прямых a и b выполнено, но возможны варианты решений

(рис. 2.23,б).

Естественно, что если одна из сторон прямого угла будет параллельна фронтальной или профильной плоскостям проекций, то и прямой угол будет проецироваться в натуральную величину соответственно на эти плоскости.

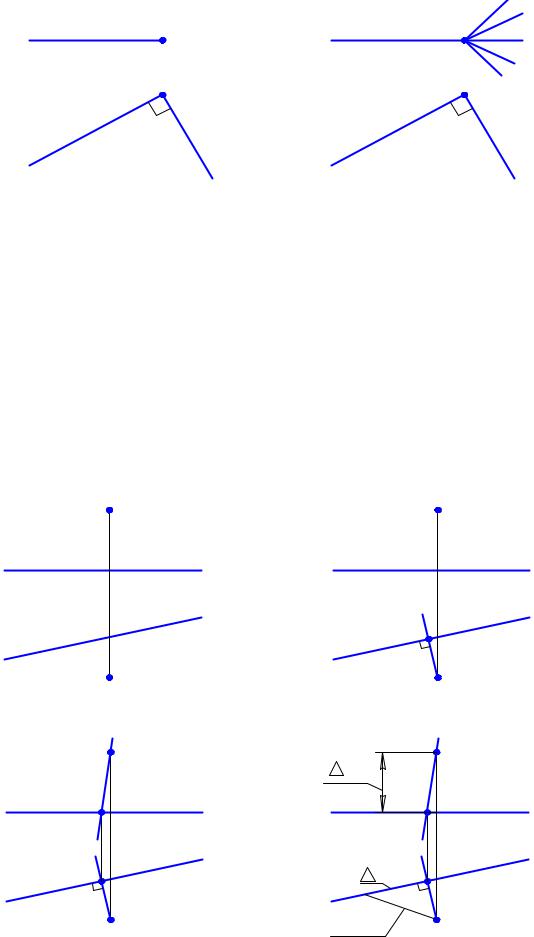
Для закрепления рассмотренного материала приведем задачу, где необходимо определить расстояние от точки A до горизонтали h (рис. 2.24,а). При этом вначале из точки A необходимо опустить перпендикуляр на прямую h. Поскольку горизонталь параллельна горизонтальной плоскости проекций, то на горизонтальной проекции прямой угол между h и перпендикуляром AB спроецируется в истинную величину (рис. 2.24,б). Точка B принадлежит горизонтали, поэтому фронтальная проекция этой точки легко определится с помощью линии проекционной связи (рис. 2.24,в). Осталось лишь определить истинную величину отрезка AB, что и сделано на рис. 2.24,г. Задача решена.

27