
- •ВВЕДЕНИЕ
- •ШАГ 1. МЕТОД ПРОЕКЦИЙ. ТОЧКА
- •1.1. Метод проекций
- •1.2. Система координат и плоскостей проекций
- •1.3. Проецирование точки на плоскости проекций
- •1.4. Точка на комплексном чертеже
- •Итоги первого шага
- •ШАГ 2. ПРЯМАЯ
- •2.1. Прямые частного положения
- •2.2. Следы прямой
- •2.4. Построение проекций отрезка заданной длины
- •2.5. Относительное положение прямых
- •2.6. Теорема о частном случае проецирования прямого угла
- •Итоги второго шага
- •ШАГ 3. ПЛОСКОСТЬ. ТОЧКА И ЛИНИИ В ПЛОСКОСТИ
- •3.1. Задание плоскости на чертеже. Точка в плоскости
- •3.2. Следы плоскости
- •3.3. Горизонталь и фронталь плоскости
- •3.4. Линии наибольшего наклона плоскости к плоскостям проекций
- •Итоги третьего шага
- •ШАГ 4. ПЛОСКОСТИ ОБЩЕГО И ЧАСТНОГО ПОЛОЖЕНИЯ
- •4.1. Проецирующая плоскость
- •4.1.1. Свойство собирательности проецирующей плоскости
- •4.1.2. О некоторых способах задания проецирующей плоскости на чертеже
- •4.1.3. Точка встречи прямой с проецирующей плоскостью
- •4.1.4. Линия пересечения двух плоскостей, одна из которых проецирующая
- •4.2. Плоскости уровня
- •Итоги четвёртого шага
- •ШАГ 5. ОТНОСИТЕЛЬНОЕ ПОЛОЖЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ ОБЩЕГО ПОЛОЖЕНИЯ
- •5.1. Точка встречи прямой с плоскостью общего положения
- •5.2. Определение видимости прямой относительно плоскости
- •5.3. Прямая, перпендикулярная плоскости
- •5.4. Прямая, параллельная плоскости
- •Итоги пятого шага
- •ШАГ 6. ОТНОСИТЕЛЬНОЕ ПОЛОЖЕНИЕ ПЛОСКОСТЕЙ
- •6.1. Пересечение двух плоскостей
- •6.2. Взаимно перпендикулярные плоскости
- •6.3. Параллельные плоскости
- •Итоги шестого шага
- •ПОМОЩЬ НА ОСТАНОВКАХ
- •ЗАКЛЮЧЕНИЕ
ШАГ 2. ПРЯМАЯ
Положение прямой в пространстве однозначно определяется двумя нетождественными точками, поэтому для задания проекций прямой достаточно задать проекции двух принадлежащих ей точек. Если точка принадлежит прямой, то ее проекция принадлежит соответствующей проекции прямой (рис. 2.1).
Прямая l проходит через точки A и B. Горизонтальная проекция точки A (A') лежит на горизонтальной проекции прямой, а фронтальная проекция – соответственно на фронтальной проекции прямой. А вот точка C не лежит на прямой l . Её проекции хотя и лежат на проекциях прямой, но не на одноименных: C' на l", а C" на l'. Не принадлежит прямой и точка D.
Если прямая не параллельна и не перпендикулярна ни одной из плоскостей проекций, то она называется прямой общего положения.
2.1. Прямые частного положения
Прямые частного положения – это прямые, параллельные или перпендикулярные какой-либо плоскости проекций. Прямые, параллельные плоскости проекций, называются прямыми уровня, а перпендикулярные – проецирующими.
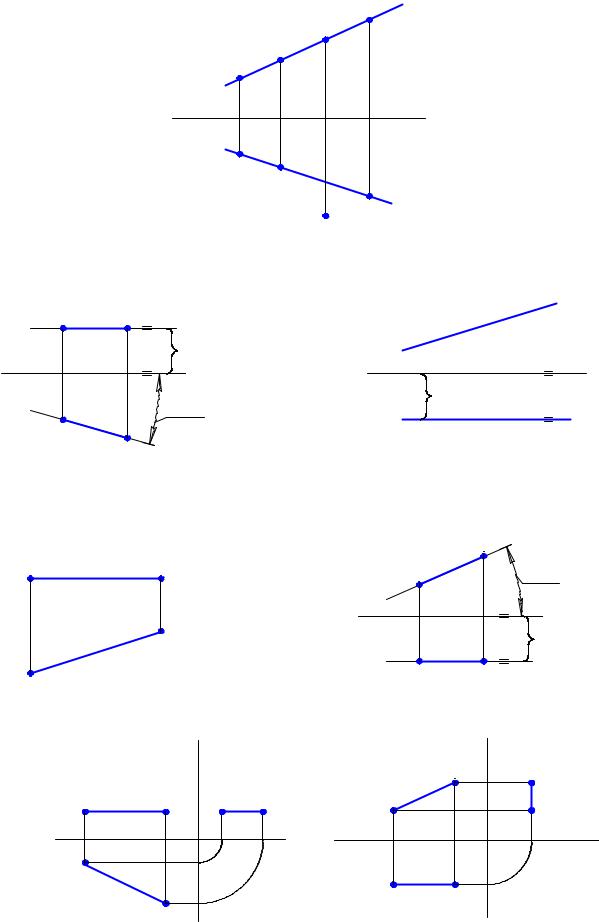
Прямая, параллельная горизонтальной плоскости проекций, называется горизонталью. У горизонтали все ее точки расположены на одинаковом расстоянии от горизонтальной плоскости проекций, следовательно, значения координаты z для всех ее точек одинаковы. Поэтому ее фронтальная проекция будет всегда параллельна оси X (рис. 2.2).
Характерной особенностью горизонтали является то, что ее отрезок проецируется на горизонтальную плоскость проекций в натуральную величину; на эту же плоскость в натуральную величину проецируется угол наклона горизонтали к фронтальной плоскости проекций – угол ϕ2
(рис. 2.2).
Обращаем внимание на то, что значения координаты z для точек горизонтали может быть как положительным, так и отрицательным, поэтому изображенная на рис. 2.3 прямая – горизонталь.
На рис. 2.4 Вы не увидели привычную ось X. Здесь изображен безосный чертеж, т.е. чертеж без указания осей системы координат. О таких чертежах уже было сказано выше. Их используют, когда нет необходимости задавать точное положение геометрического объекта относительно плоскостей проекций. Так, где бы мы ни провели оси X, Y, Z на рис. 2.4, прямая AB останется горизонталью.
Прямая, параллельная фронтальной плоскости проекций, называется фронталью. Для всех ее точек характерно постоянство координаты y, так как именно эта координата определяет расстояние от точки до фронтальной плоскости проекций. По аналогии с горизонталью у фронтали фронтальная проекция отрезка и есть его натуральная величина. В истинную величину проецируется и угол ϕ1 – угол наклона прямой к горизонтальной плоскости проекций (рис. 2.5).
Прямая, параллельная профильной плоскости проекций, носит название профильной прямой или профили. Все её точки имеют постоянную координату х. На профильной плоскости проекций мы получим истинную величину отрезка прямой линии и углов его наклона к горизонтальной и фронтальной плоскостям проекций.
На рис. 2.6 и 2.7 в трех проекциях изображены отрезки горизонтали (AB) и фронтали (CD). На рис. 2.8 показана прямая, перпендикулярная горизонтальной плоскости проекций, – это го-
ризонтально-проецирующая прямая. Напомним, что с помощью таких прямых строились проекции точки. Горизонтальная проекция горизонтально-проецирующей прямой есть точка. Проецирующие прямые обладают свойством собирательности, т.е. все точки, принадлежащие горизон- тально-проецирующей прямой, имеют горизонтальную проекцию, совпадающую с горизонтальной проекцией самой прямой.
Аналогичными свойствами обладают и фронтально-проецирующая прямая (рис. 2.9), и про- фильно-проецирующая.
Обратите внимание: проецирующие прямые – это одновременно и прямые уровня. Так, гори- зонтально-проецирующая прямая является фронталью и профилью, а фронтально-проецирующая
– горизонталью и профилью.
17
D"
C'
A"
x
A'
C"
D'
Рис. 2.1
A" |
B" |
h" |
x |
|
Z-const |
|
è. |
j2 |
|
|
|
||
|
â. |
|
|
A' |
AB |
h' |
|
B' |
|||
|
|||
|
|
||
|
Рис. 2.2 |
|
A" B"
B'
A' Рис. 2.4
A" h" |
B" A"'h"' B"' |
A' h'
B'
Рис. 2.6
B" l"
B' l'
h'
x
Z-const
h"
Рис. 2.3
|
|
|
|
D |
D" |
f" |
|
|
|
|
|
|
|
|
|
|
.C |
|
|
|
|
|
.â |
|
|
j1 |
|
|
Ñ" |
è |
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
y-const |
|
C' |
|
|
|
D' |
f' |
|
|
|
|
|
||
|
|
|
|
Рис. 2.5 |
|
|
|
f" |
D" |
|
D"' |
||
Ñ" |
|
|
|
f"' |
||
|
|
|
|
|
|
C"' |
f'
C' D'
Рис. 2.7
18
|
l" |
m" 1" 2" 3" |
|
1" |
|
|
x |
3' |
x |
2" |
2' |
|
3" |
1' m' |
|
l' 1' 2' 3' |
|
|
|
|
|
Рис. 2.8 |
Рис. 2.9 |
2.2. Следы прямой
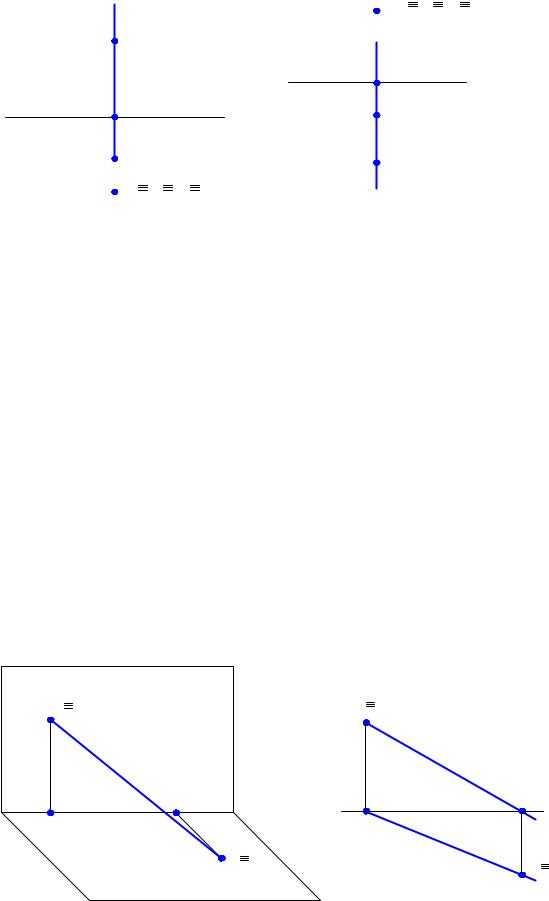
Следами прямой называют точки ее пересечения с плоскостями проекций. Часто используют следующие обозначения: H – горизонтальный след, F – фронтальный след, W – профильный след.
След прямой – точка двоякой принадлежности. Прежде всего, это точка на прямой, т.е. проекции следа лежат на одноименных проекциях прямой. С другой стороны, след – это точка в плоскости проекций, т.е. точка, одна из координат которой равна нулю. Характерной особенностью таких точек является то, что они совпадают с одной из своих проекций.
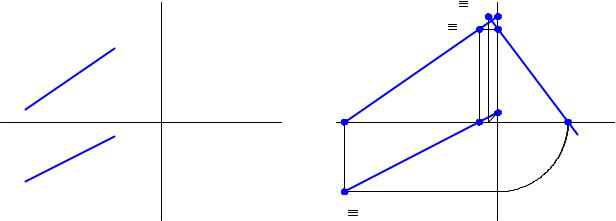
Таким образом, горизонтальный след – это точка на прямой, координата z которой равна нулю; фронтальный след – это точка на прямой, где y =0, а у профильного следа x=0. На рис. 2.10,а показаны горизонтальный и фронтальный следы прямой, а на рис. 2.10,б построены проекции этих следов. На рис. 2.11,а представлены исходные данные для решения задачи по нахождению проекций всех трех следов прямой m.
Построение проекций следов начинаем с построения горизонтальной и фронтальной проекций следов H и F (рис. 2.11,б) – это построение аналогично выполненному на рис. 2.10,б. Затем можно построить горизонтальную и фронтальную проекции профильного следа W как точки на прямой m, у которой координата x=0. Зная горизонтальные и фронтальные проекции следов, несложно построить их профильные проекции.
Если соединить профильные проекции следов H и F, можно построить профильную проекцию прямой m, хотя для построения проекций следов она, в принципе, не нужна. При правильном построении профильная проекция прямой должна пройти через профильную проекцию профильного следа.
F |
p2 |
F |
F" |
|
|
F" |
|
|
|||
|
l |
|
|
l" |
|
|
|
|
|
|
|
F' |
H" |
|
F' |
H" |
|
|
|
|
|
l' |
|
|
H |
H' |
|
H |
H' |
|
|
p1 |
|
||
|
|
|
|
|
|
|
à |
Рис. 2.10 |
|
á |
|
|
|
|
|
|
|
|
|
19 |
|
|
|
|
W |
W"'W" |
|
|
|
F |
F" |
F"' |
|
m" |
m" |
|
m"' |
|
H" |
|
F' |
W' |
H"' |
m' |
m' |
|
|
|
H |
H' |
á |
|
|
à |
|
|
|
|
Рис. 2.11 |
|
|
|
|
2.3.Определение истинной величины отрезка прямой и углов наклона прямой
кплоскостям проекций
Если прямая является линией частного положения, данная задача решается простым указанием на чертеже искомых величин, что было рассмотрено ранее на примере отрезков горизонтали и фронтали.
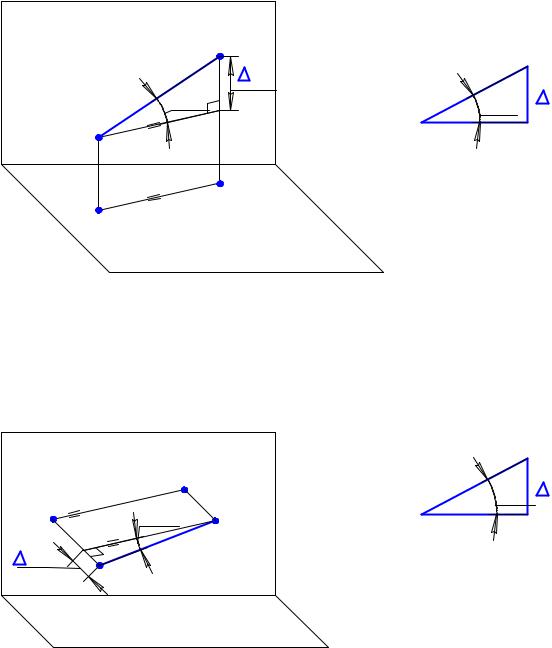
Рассмотрим проецирование отрезка AB прямой общего положения (рис. 2.12,а). Этот отрезок не проецируется ни на одну из плоскостей проекций в натуральную (истинную) величину (и.в.), т.е. и.в. AB не равна и.в. A'B' и не равна и.в. A"B".
Нам удастся определить истинную величину отрезка AB, если на чертеже (пока не важно, как и где) мы сумеем построить прямоугольный треугольник ABC. Тогда его гипотенуза AB – истинная величина отрезка, а угол ϕ1 – угол наклона отрезка к горизонтальной плоскости проекций. Как
известно, прямоугольный треугольник можно построить в истинную величину, если известны величины его катетов.
Катет AC есть не что иное, как величина горизонтальной проекции отрезка AB, а катет BC по величине равен разности расстояний точек A и B от горизонтальной плоскости проекций, т.е. величине z . Таким образом, выявляется следующая схема определения истинной величины отрезка AB и угла наклона его к горизонтальной плоскости проекций (рис. 2.12,б).
Можно рассмотреть проецирование отрезка AB несколько иначе (рис. 2.13,а). В этом случае мы получим схему определения истинной величины отрезка и угла наклона его к фронтальной плоскости проекций, изображенную на рис. 2.13,б.
Для определения истинной величины отрезка и угла наклона его к профильной плоскости проекций используется схема, приведенная на рис. 2.14,б, а иллюстрация к ней – на рис. 2.14,а.
Таким образом, можно сформулировать следующее правило: для того чтобы определить ис-
тинную величину отрезка прямой и угол наклона его к плоскости проекций π, необходимо построить прямоугольный треугольник, один из катетов которого равен проекции отрезка на плоскость проекций π, а другой равен разности расстояний концов отрезка до этой же плоскости проекций. Гипотенуза такого треугольника и есть истинная величина отрезка. Угол между гипотенузой и катетом, равным проекции отрезка на плоскость проекций π, и есть истинная величина угла наклона прямой к этой плоскости проекций.
Важным этапом определения истинной величины отрезка является определение разности координат его концов. Если заданы горизонтальная и фронтальная проекции, то пример их определения иллюстрируется рис. 2.15. На рис. 2.16 приведен пример для случая, когда заданы фронтальная и профильная проекции.
Рассмотрим пример определения истинной величины отрезка (рис. 2.17,а). Построение можно начать с определения величины z , а затем построить прямоугольный треугольник, первый катет
20
которого равен горизонтальной проекции отрезка, а второй – уже определенной величине z . Гипотенуза такого прямоугольного треугольника и есть истинная величина отрезка, а угол между гипотенузой и первым катетом равен углу наклона отрезка к горизонтальной плоскости проекций.
На рис. 2.17,б построение начато с катета, величина которого равна z , а затем построен катет, величина которого равна величине горизонтальной проекции отрезка. Обратите внимание на то, что в данном случае можно работать на безосном чертеже, так как для определения истинной величины отрезка сами координаты не нужны, а нужны лишь разности координат его концов.
p2
B
z
f1
A C
B'
A'
p1
à
Рис. 2.12
p2
B" A" j2 B
y
A
p1
à
è.â.
j1 z
ãîð.ïð.
á
è.â. j2 y
фронт.пр.
á
Рис. 2.13
21

p2
B |
B"' |
è.â. |
j3 õ |
j3 |
|
ïðîô.ïð. |
|
A |
|
A"' |
|
|
á |
|
|
|
|
|
|
x |
|
p3 |
|
|
|
|
p1
à
Рис. 2.14
B"
z
A"
x
x
A' |
y |
B'
Рис. 2.15
B" B"'
z
x |
A" |
A"' |
|
|
|
|
x |
y |
Рис. 2.16
22
