
- •ВВЕДЕНИЕ
- •ШАГ 1. МЕТОД ПРОЕКЦИЙ. ТОЧКА
- •1.1. Метод проекций
- •1.2. Система координат и плоскостей проекций
- •1.3. Проецирование точки на плоскости проекций
- •1.4. Точка на комплексном чертеже
- •Итоги первого шага
- •ШАГ 2. ПРЯМАЯ
- •2.1. Прямые частного положения
- •2.2. Следы прямой
- •2.4. Построение проекций отрезка заданной длины
- •2.5. Относительное положение прямых
- •2.6. Теорема о частном случае проецирования прямого угла
- •Итоги второго шага
- •ШАГ 3. ПЛОСКОСТЬ. ТОЧКА И ЛИНИИ В ПЛОСКОСТИ
- •3.1. Задание плоскости на чертеже. Точка в плоскости
- •3.2. Следы плоскости
- •3.3. Горизонталь и фронталь плоскости
- •3.4. Линии наибольшего наклона плоскости к плоскостям проекций
- •Итоги третьего шага
- •ШАГ 4. ПЛОСКОСТИ ОБЩЕГО И ЧАСТНОГО ПОЛОЖЕНИЯ
- •4.1. Проецирующая плоскость
- •4.1.1. Свойство собирательности проецирующей плоскости
- •4.1.2. О некоторых способах задания проецирующей плоскости на чертеже
- •4.1.3. Точка встречи прямой с проецирующей плоскостью
- •4.1.4. Линия пересечения двух плоскостей, одна из которых проецирующая
- •4.2. Плоскости уровня
- •Итоги четвёртого шага
- •ШАГ 5. ОТНОСИТЕЛЬНОЕ ПОЛОЖЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ ОБЩЕГО ПОЛОЖЕНИЯ
- •5.1. Точка встречи прямой с плоскостью общего положения
- •5.2. Определение видимости прямой относительно плоскости
- •5.3. Прямая, перпендикулярная плоскости
- •5.4. Прямая, параллельная плоскости
- •Итоги пятого шага
- •ШАГ 6. ОТНОСИТЕЛЬНОЕ ПОЛОЖЕНИЕ ПЛОСКОСТЕЙ
- •6.1. Пересечение двух плоскостей
- •6.2. Взаимно перпендикулярные плоскости
- •6.3. Параллельные плоскости
- •Итоги шестого шага
- •ПОМОЩЬ НА ОСТАНОВКАХ
- •ЗАКЛЮЧЕНИЕ
1.4. Точка на комплексном чертеже
Перейдем к рассмотрению комплексного чертежа, на котором можно построить сразу все три проекции. Метод получения такого чертежа был разработан французским ученым Гаспаром Монжем, а комплексный чертеж получил название эпюра Монжа.
Рассмотрев отдельно проекции точек на три взаимно перпендикулярные плоскости проекций, совместим на одном чертеже изображение системы координат, так как предварительная работа по совмещению плоскостей проекций с плоскостью чертежа уже проделана.
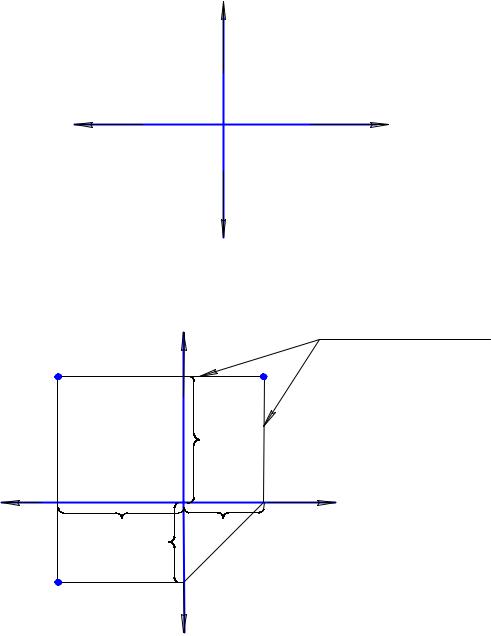
Обратите внимание (рис. 1.12), что на комплексном чертеже изображение оси x для горизонтальной и фронтальной плоскостей проекций совпадает, так же как совпадает изображение оси z для фронтальной и профильной плоскостей проекций, а ось Y как бы раздвоилась: для горизонтальной проекции она направлена вниз, а для профильной – вправо. Это обстоятельство вначале вызывает некоторые трудности при работе с комплексным чертежом, которые легко преодолеть, если не забывать, что в пространстве ось Y одна и координата y для горизонтальной проекции всегда равна координате y для профильной.
Рассмотрим комплексный чертеж, где построены три проекции точки A(x,y,z), расположенной в I октанте (рис. 1.13).
|
(-yp1 ) |
z |
|
|
x |
|
|
|
yp3 |
(-yp3 ) |
|
|
|
(-x) |
|
(-z) |
yp1 |
|
|
|
Рис. 1.12 |
|
|
|
|
z |
линии |
проекцион- |
|
|
íîé |
связи |
||
A" |
|
|||
|
A"' |
|
|
|
|
A |
|
|
|
|
z |
|
|
|
x |
|
yp3 |
|
|
xA |
yA |
|
|
|
|
|
|
||
|
A |
|
|
|
|
y |
|
|
|
A' |
yp1 |
|
|
|
|
|
|
|
|
|
Рис. 1.13 |
|
|
|
|
|
10 |
|
|
Поскольку положение точки в пространстве однозначно определяется тремя координатами, а каждая из проекций задает значение двух координат, то легко сделать вывод, что положение точки в пространстве однозначно определяется двумя любыми проекциями.
Кроме того, каждая пара проекций связана какой либо координатой. Так, проекции A'(x,y) и A"(x,z) связаны координатой x, проекции A"(x,z) и A"'(y,z) – координатой z, а A'(x,y) и A"'(y,z) – координатой y.
Таким образом, можно отметить, что при любых значениях координат точки (как положительных, так и отрицательных) справедливо следующее утверждение:
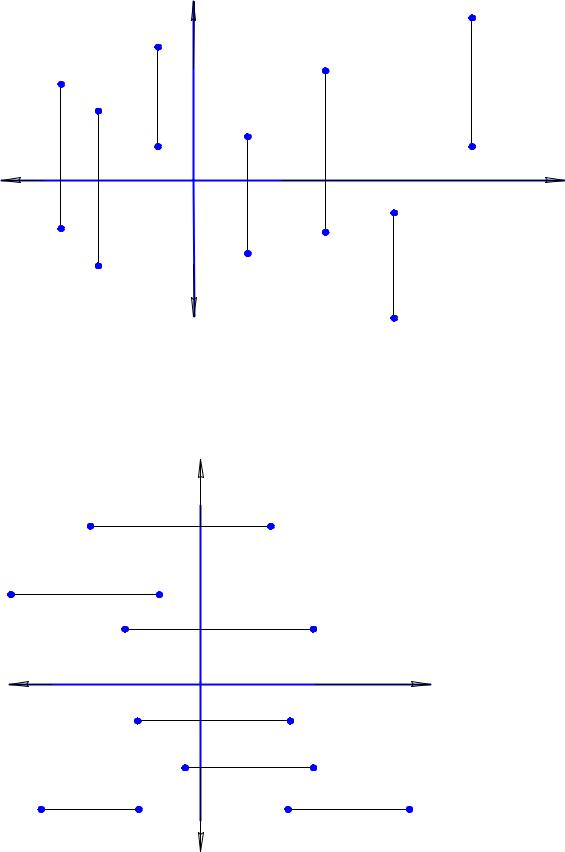
а) горизонтальная и фронтальная проекции точки однозначно определяют положение точки в пространстве и, поскольку связаны координатой x, лежат на одной прямой (линии проекционной связи), перпендикулярной оси X (рис. 1.14).
б) фронтальная и профильная проекции точки однозначно определяют положение точки в пространстве и, поскольку связаны координатой z, лежат на одной прямой (линии проекционной связи), перпендикулярной оси Z (рис. 1.15).
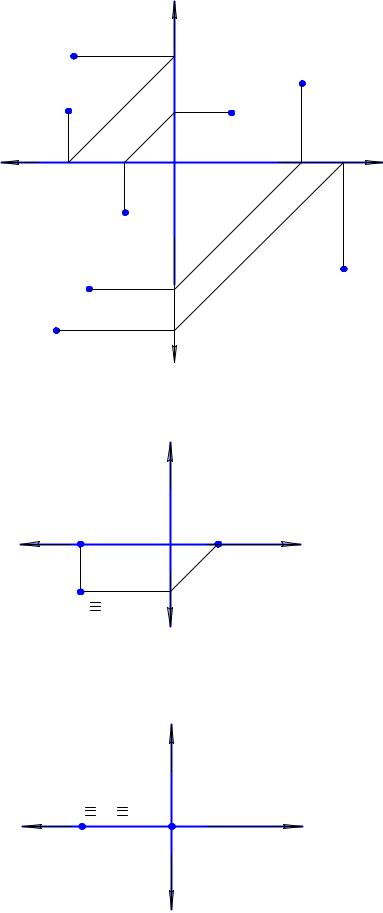
в) горизонтальная и профильная проекции точки однозначно определяют положение точки в пространстве и, поскольку связаны координатой y, лежат на одной прямой (линии проекционной связи), перпендикулярной раздвоенной оси Y (рис. 1.16).
На рис. 1.17 построены проекции точки М, у которой координата z равна нулю. Это означает, что, поскольку координата z задает удаление точки от горизонтальной плоскости проекций, заданная точка М лежит в горизонтальной плоскости проекций. В этом случае на чертеже могут быть указаны не только проекции точки, но и сама точка, совпадающая со своей горизонтальной проекцией.
Рис. 1.18 иллюстрирует проекции точки N, находящейся на оси X, так как ее координаты y и z имеютнулевыезначения. Здесьсовпадаютгоризонтальная, фронтальнаяпроекцииточкиисаматочкаN.
И, наконец, отметим, что рассмотренный комплексный чертеж является обратимым, так как позволяет решать как прямую задачу (по заданным координатам построить проекции точки), так и обратную (по заданным проекциям определить координаты точки).
Исходными данными для прямой задачи являются координаты точки, заданные в виде последовательности трех чисел (координат x, y и z), заключенных в скобки.
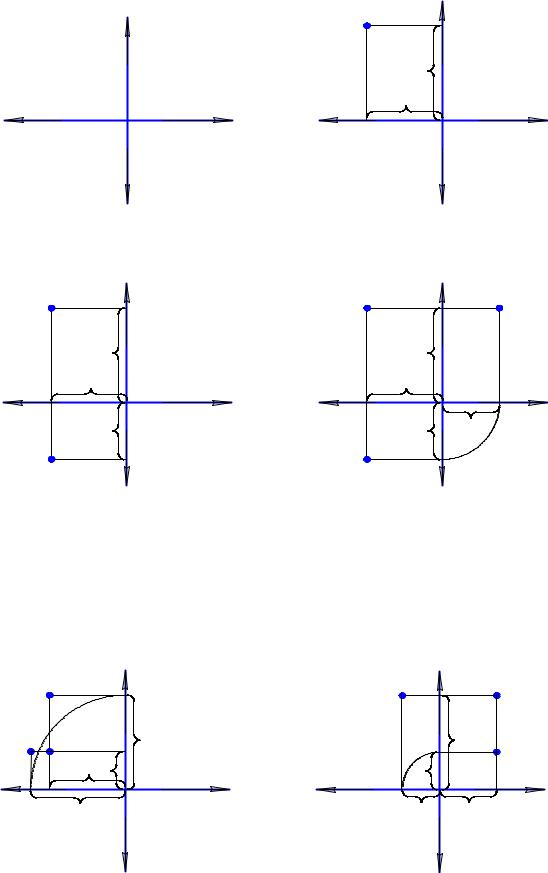
Например, необходимо построить проекции точки A(20,15,25) (рис. 1.19,а). Рекомендуется следующий порядок построения. Сначала строится фронтальная проекция точки по координатам x=20, z=25 (рис. 1.19,б), затем по координатам x=20, y=15 – горизонтальная проекция точки (рис. 1.19,в). Обратите внимание, что для горизонтальной проекции ось Y направлена вниз.
Профильная проекция точки строится по координатам y=15, z=25, при этом ось Y направлена вправо (рис. 1.19,г). На рис. 1.20 приведены результаты построения проекций точки B, находящейся во II октанте, а на рис. 1.21 – точки C, которая находится в VI октанте.
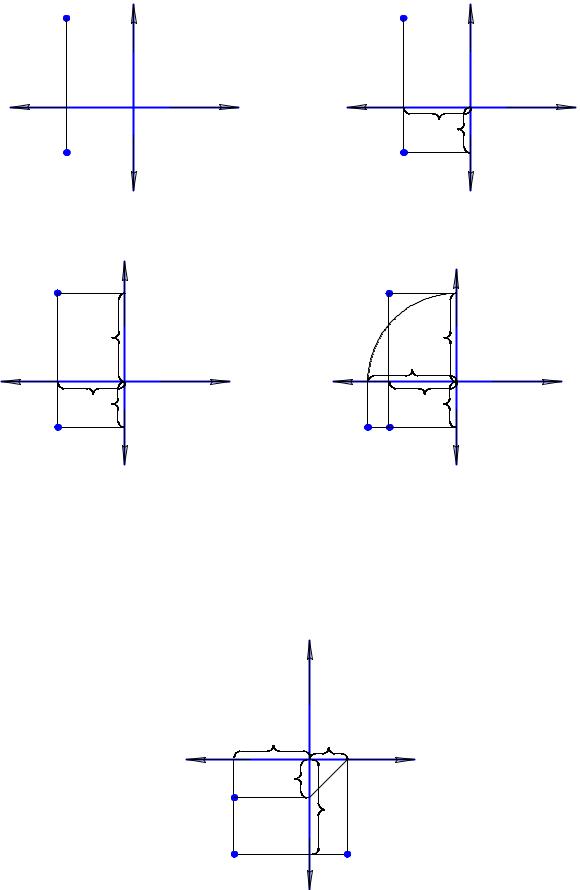
Обратная задача – по заданным проекциям определить координаты точки. Для этого обычно задают две проекции точки, а задачу дополняют требованием построить недостающую проекцию. Рассмотрим такую задачу на примере точки D, две проекции которой заданы на рис.1.22,а. По фронтальной проекции точки определяются координаты x и z (рис. 1.22,б), а по горизонтальной проекции – координата y (рис. 1.22,в), которая указывается вдоль оси yπ1 . У точки D координата
x > 0, y < 0, z < 0 – точка лежит в III октанте. Для построения недостающей профильной проекции необходимо координату y отложить на оси yπ3 и построить D′′′ по координатам y и z (рис. 1.22,г).
Одним из этапов построения чертежа является перенос координаты y между осями yπ1 и yπ3 (мы помним, что в пространстве ось Y всего одна). В рассмотренных выше примерах этот пе-
ренос осуществлялся с помощью дуги окружности, центр которой находится в начале координат. На рис. 1.23 вместо дуги использовалась ее хорда. На рис. 1.24,а для переноса координаты y использовалась прямая k0, называемая постоянной прямой эпюра Монжа. Эта прямая проходит через начало координат под углом 45°.
Обратите внимание, что линии проекционной связи на чертеже, где использована постоянная прямая эпюра Монжа, образуют в общем случае прямоугольник (рис. 1.24,б), причем в ряде случаев оси системы координат не изображаются, образуя безосный чертеж (рис. 1.24,в). Такие чертежи используют, когда нет необходимости задавать точное положение геометрического объекта относительно плоскостей проекций. Если при работе с безосным чертежом возникнет необходимость провести ось, то это можно сделать где угодно, помня о направлении.
При использовании на безосном чертеже постоянной прямой эпюра Монжа необходимо иметь в виду, что такая прямая на чертеже может быть только одна (рис. 1.25).
11
z |
|
G' |
C" |
E" |
|
A" |
A"(x,z) |
|
B' |
|
A'(x,y) |
|
|
|
C' |
D' |
G" |
x |
|
|
|
yp3 |
|
A' |
E' |
F" |
D" |
|
|
B" |
|
|
|
|
|
yp1 |
|
F' |
|
|
|
|
Рис. 1.14 |
|
|
|
z |
|
|
B"' |
B" |
|
C" |
C"' |
|
A"(x,z) |
|
A"'(y,z) |
||
|
A" |
A"' |
|
|
|
||
x |
D" |
D"' |
yp3 |
|
|
||
|
E"' |
E" |
|
F"' |
F" |
G"' |
G" |
|
|
yp1 |
|
|
|
Рис. 1.15 |
|
12
|
|
|
|
z |
|
|
|
|
D' |
|
|
|
|
|
A'(x,y) |
|
|
|
|
|
|
A"' |
|
|
|
|
|
|
|
A"'(y,z) |
|
|
D"' |
|
|
|
C' |
|
|
|
|
|
|
|
|
||
x |
|
|
|
|
|
|
yp3 |
|
|
C"' |
|
|
|
|
|
|
A' |
|
|
|
|
B"' |
|
|
B' |
|
|
|
|
|
|
|
|
|
|
yp1 |
|
|
|
|
|
|
|
|
Рис. 1.16 |
|
|
|
M(x,y,0) |
|
z |
|
|
A'(x,y) |
|
|
|
|
|
A"'(y,z) |
|||
|
|
|
|
|
|||
x |
M" |
|
|
M"' |
yp3 |
|
|
|
|
|
|
|
|
|
|
|
M |
M' |
|
yp1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 1.17 |
|
|
|
N(x,0,0) |
|
z |
|
|
|
|
x |
N |
N' |
N" |
N"' |
|
yp3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
yp1 |
|
|
|
|
|
|
|
|
Рис. 1.18 |
|
|
|
|
|
|
|
13 |
|
|
|
|
A(20,15,25) |
A" |
|
|
|
|
|
z |
|
z |
|
|
|
|
|
|
|
||
|
|
|
|
z |
|
|
x |
|
yp3 |
x |
x |
|
yp3 |
|
|
|
|
|
||
|
|
yp1 |
|
|
yp1 |
|
|
|
a |
|
|
á |
|
A" |
|
z |
A" |
|
z |
A"' |
|
|
|
||||
|
|
|
|
|
||
|
|
z |
|
z |
|
|
x |
|
x |
x |
x |
|
yp3 |
|
|
yp3 |
|
|
|
|
|
|
yp1 |
|
yp1 |
yp3 |
|
A' |
|
yp1 |
A' |
|
yp1 |
|
|
|
â |
|
|
ã |
|
|
|
|
Рис. 1.19 |
|
|
|
|
B(20,-25,10) |
|
C(-15,-10,25) |
|||
B' |
|
z |
|
C"' |
|
C" |
|
|
|
|
|||
B"' |
B" |
yp1 |
|
|
z |
C' |
x |
|
x z |
x |
yp1 |
|
|
|
|
yp3 |
||||
|
|
yp3 |
|
yp3 |
x |
|
|
yp3 |
|
|
|||
|
|
|
|
|
||
|
|
yp1 |
|
|
yp1 |
|
|
|
Рис. 1.20 |
|
Рис. 1.21 |
|
|
|
|
|
14 |
|
|
|
D' |
z |
|
|
D' |
z |
|
|
|
|
|
|
x |
yp3 |
|
|
x |
yp3 |
|
|
|
x z |
||
|
|
|
|
|
|
D" |
yp1 |
|
|
D" |
yp1 |
|
|
|
|
||
|
a |
|
|
á |
|
D' |
z |
|
|
D' |
z |
yp1 |
|
|
|
yp1 |
|
|
|
x |
yp3 |
|
|
x |
yp3 |
|
yp3 |
||
x z |
|
|
x z |
||
|
|
|
|
||
D" |
yp1 |
|
|
D"' D" |
yp1 |
|
|
|
|
||
|
â |
|
|
ã |
|
|
|
|
Рис. 1.22 |
|
|
|
|
|
z |
|
|
|
x |
x |
yp3 |
|
|
|
|
yp1 |
yp3 |
|
|
|
E' |
|
|
||
|
|
z |
|
|
|
|
|
|
|
|
|
|
E" |
|
|
E"' |
|
|
|
|
yp1 |
|
|
|
|
|
Рис. 1.23 |
|
|
|
|
|
15 |
|
|
