- •Кафедра энергосбережения, гидравлики и теплотехники
- •Введение
- •Практическое занятие №1 Планирование производственно-хозяйственной деятельности предприятия
- •1Теоретическая часть
- •2 Пример решения
- •Эмпирические данные
- •3 Индивидуальные задания
- •Классы функций
- •2 Пример решения
- •Результаты испытаний
- •3 Индивидуальные задания
- •Энергетические характеристики
- •4 Контрольные вопросы
- •Практическое занятие №3
- •1Теоретическая часть
- •Корреляционная таблица
- •2 Пример решения
- •Исходные данные
- •Вспомогательная таблица
- •3 Индивидуальные задания
- •Потери тепла в котельном агрегате
- •4 Контрольные вопросы
- •Практическое занятие №4
- •1 Теоретическая часть
- •Матрица планирования
- •2 Пример решения
- •3 Индивидуальные задания
- •4 Контрольные вопросы
- •Практическое занятие №5
- •1 Теоретическая часть
- •2 Пример решения
- •3 Индивидуальные задания
- •Исходные данные
- •4 Контрольные вопросы
- •Лабораторная работа №1 Оценка экономической эффективности инвестиций в энергосберегающие мероприятия.
- •1Теоретическая часть
- •2 Индивидуальные задания
- •Денежные потоки
- •3 Порядок выполнения работы
- •4 Контрольные вопросы
- •Лабораторная работа №2 Выбор приоритетных инвестиционных проектов с одинаковыми сроками реализации
- •1 Теоретическая часть
- •2 Исходные данные
- •4 Контрольные вопросы
- •Исходные данные
- •2 Исходные данные
- •Денежные потоки проекта а
- •Денежные потоки проекта б
- •Распределение денежных доходов по годам для проекта а
- •Распределение денежных доходов по годам для проекта б
- •3 Порядок выполнение работы
- •Сценарии оценки чувствительности инвестиционного проекта
- •Сценарии оценки чувствительности инвестиционного проекта
- •Результаты анализа чувствительности проекта
- •2 Исходные данные
- •3 Выполнение работы
- •4 Контрольные вопросы
- •Лабораторная работа №5 Имитационное моделирование в инвестиционном проектировании
- •1 Теоретическая часть
- •2 Исходные данные
- •Исходные данные
- •3 Порядок выполнения работы
- •Значения функции спроса.
- •Инвестиции, амортизационные отчисления и производственная мощность
- •Прибыль от реализации проекта
- •Чистый дисконтированный доход
- •4 Контрольные вопросы
- •Содержание
- •Энергетическое планирование и финансы в сфере энергосбережения
- •Редактор
- •220006. Минск, Свердлова, 13а.
Корреляционная таблица
|
Y X |
y1 |
y2 |
… |
yi |
ni |
|
x1 |
m11 |
m12 |
… |
m1l |
n1 |
|
x2 |
m21 |
m22 |
… |
m2l |
n2 |
|
|
|
|
|
|
|
|
xk |
mk1 |
mk2 |
… |
mkl |
nk |
|
mj |
m1 |
m2 |
… |
ml |
n |
В случае, когда случайные величины являются непрерывными (т.е. могут принимать любое значение из соответствующих интервалов), составляется интервальная корреляционная таблица.
Условным среднимназывают среднее арифметическое значенийY, соответствующих значениюX=x. Например,
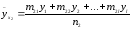 .
.
Корреляционной зависимостьюYотXназывают зависимость:
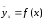 (8)
(8)
Уравнение
(8) называют эмпирическим
уравнением регрессииYнаX;
функцию f(x) называютэмпирическойрегрессиейYнаX, а ее график -
линией регрессииYна X.
называютэмпирическойрегрессиейYнаX, а ее график -
линией регрессииYна X.
Аналогично
определяются условная средняя
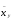 и корреляционная зависимостьXотY:
и корреляционная зависимостьXотY:
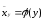 (9)
(9)
Распределение
системы (X,Y)характеризуется числовыми параметрами:
математическими ожиданиями компонентmx,
my;
дисперсиями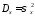 ,
,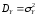 ;
корреляционным моментом (ковариацией)
;
корреляционным моментом (ковариацией)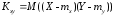 ;
коэффициентом корреляции
;
коэффициентом корреляции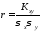 ,
,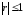 .
.
Здесь и дальше, будем считать, что двумерная случайная величина (X,Y) распределена нормально, тогда уравнения линейной регрессии YнаXи X наYимеют вид:
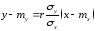 и
и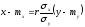
По корреляционной таблице 6, найдем оценки параметров линейной регрессии:
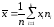 ;
;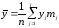 ;
(10)
;
(10)
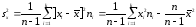 ;
(11)
;
(11)
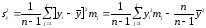 ;
(12)
;
(12)
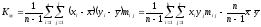 ;
(13)
;
(13)
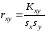 - выборочный коэффициент корреляции .
- выборочный коэффициент корреляции .
Выборочный
коэффициент корреляции
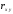 характеризует тесноту линейной связи
между
характеризует тесноту линейной связи
между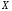 и
и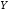 .
Если
.
Если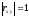 ,
то элементы выборки
,
то элементы выборки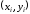 ,
,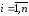 лежат на прямой линии, а
лежат на прямой линии, а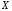 и
и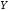 считаются практически линейно зависимы.
Чем ближе
считаются практически линейно зависимы.
Чем ближе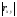 к 1, тем связь сильнее; чем ближе
к 1, тем связь сильнее; чем ближе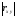 к 0, тем связь слабее. ЕслиXиYнезависимы, то
к 0, тем связь слабее. ЕслиXиYнезависимы, то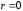 .
.
Эмпирическая функция линейной регрессии YнаXиXнаYсоответственно задаётся уравнениями
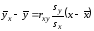 ;
;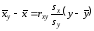 .
.
Замечание
1.Если построить на одном корреляционном
поле две линии регрессииYнаXиXнаY, то они пересекутся
в точкеO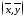 ,
и угол между этими прямыми тем меньше,
чем ближе коэффициент корреляции к
,
и угол между этими прямыми тем меньше,
чем ближе коэффициент корреляции к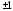 .
.
Замечание 2.В случае, когда данные наблюденийXиYзаписаны в виде интервальной корреляционной таблицы в формулах (10) – (13) вместоxiиyiобычно берут середины, соответствующих интервалов.
Для проверки соответствия линейной регрессии результатам наблюдений вычисляется наблюдаемое значение критерия
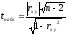
и
по таблице критических точек
распределения Стьюдента (таблица 7) по
заданному уровню значимости α и числу
степеней свободы k=n–2
, находится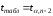 .
Затем сравнивается наблюдаемое значение
критерия с табличным.
.
Затем сравнивается наблюдаемое значение
критерия с табличным.
Таблица 7
t-Распределение Стьюдента.
|
Число степеней свободы, υ |
Уровень значимости,α |
Число степеней свободы, υ |
Уровень значимости,α | ||
|
0,1 |
0,05 |
0,1 |
0,05 | ||
|
1 |
6,31 |
12,7 |
17 |
1,74 |
2,11 |
|
2 |
2,92 |
4,3 |
18 |
1,73 |
2,10 |
|
3 |
2,35 |
3,18 |
19 |
1,73 |
2,09 |
|
4 |
2,13 |
2,78 |
20 |
1,73 |
2,09 |
|
5 |
2,01 |
2,57 |
21 |
1,72 |
2,06 |
|
6 |
1,94 |
2,45 |
22 |
1,72 |
2,07 |
|
7 |
1,89 |
2,36 |
23 |
1,71 |
2,07 |
|
8 |
1,86 |
2,31 |
24 |
1,71 |
2,06 |
|
9 |
1,83 |
2,26 |
25 |
1,71 |
2,06 |
|
10 |
1,81 |
2,23 |
26 |
1,71 |
2,06 |
|
11 |
1,80 |
2,2 |
27 |
1,71 |
2,05 |
|
12 |
1,78 |
2,18 |
28 |
1,70 |
2,05 |
|
13 |
1,77 |
2,16 |
29 |
1,70 |
2,05 |
|
14 |
1,76 |
2,14 |
30 |
1,70 |
2,04 |
|
15 |
1,75 |
2,13 |
40 |
1,68 |
2,02 |
|
16 |
1,75 |
2,12 |
60 |
1,67 |
2,00 |
|
|
|
|
120 |
1,66 |
1,98 |
Если
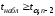 ,
то гипотеза о некоррелированности
составляющихXиYотвергается. Если же
,
то гипотеза о некоррелированности
составляющихXиYотвергается. Если же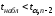 ,
то нет основания отвергать гипотезу о
некоррелированности случайных величинXиY.
,
то нет основания отвергать гипотезу о
некоррелированности случайных величинXиY.