2 Пример решения

Найти эмпирическую зависимость по данным, приведенным в таблице 1.

Таблица 1

Эмпирические данные

x	24	26	28	30	32	34	36	38	40	42
y	49	53	54	56	61	62	65	69	72	76

Решение

Нахождение эмпирических формул методом наименьших квадратов можно осуществлять в среде Excel, используя:

• функции СТЕПЕНЬ, ПРОИЗВЕД, СУММ, СУММКВ, СУММПРОИЗВ,

• формулы массива МОБР, МУМНОЖ,

• графический анализ с помощью линий тренда.

Рассмотрим на конкретных примерах, как работают эти функции (рис.1).

1. Внесем данные задачи в ячейки «B4:B13» и «C4:C13».

2. Вычислим x_i² , введя в ячейку «D4» формулу «=B4*B4»

и затем скопировав ее в ячейки «D5:D13» (направив указатель мыши на черный квадрат в правом нижнем углу ячейки, чтобы он принял вид черного крестика, и протащив в ячейкуD6 и т.д.).

Аналогично найдем произведения x_i y_iи результат запишем в ячейках «E4:E13».

Эти же результаты можно получить, используя функции СТЕПЕНЬ и ПРОИЗВЕД в категории Математические Мастера функций.

3. Найдем сумму значений в ячейках «B4:B13» и результат запишем в ячейку «B14». Для этого выделим соответствующие ячейки и нажмем пиктограмму суммирование на Панели инструментов.

Для суммирования элементов массива можно воспользоваться функциями СУММ, СУММКВ, СУММПРОИЗВ в категории Математические Мастера функций.

4. Система (2) для нашего примера примет вид:

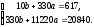
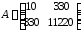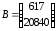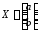Обозначим − матрица системы,− столбец свободных членов,− столбец неизвестных.

Систему решим матричным методом по формуле: 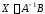, выполнив действия, записанные ниже.

Рис.1 – Пример решения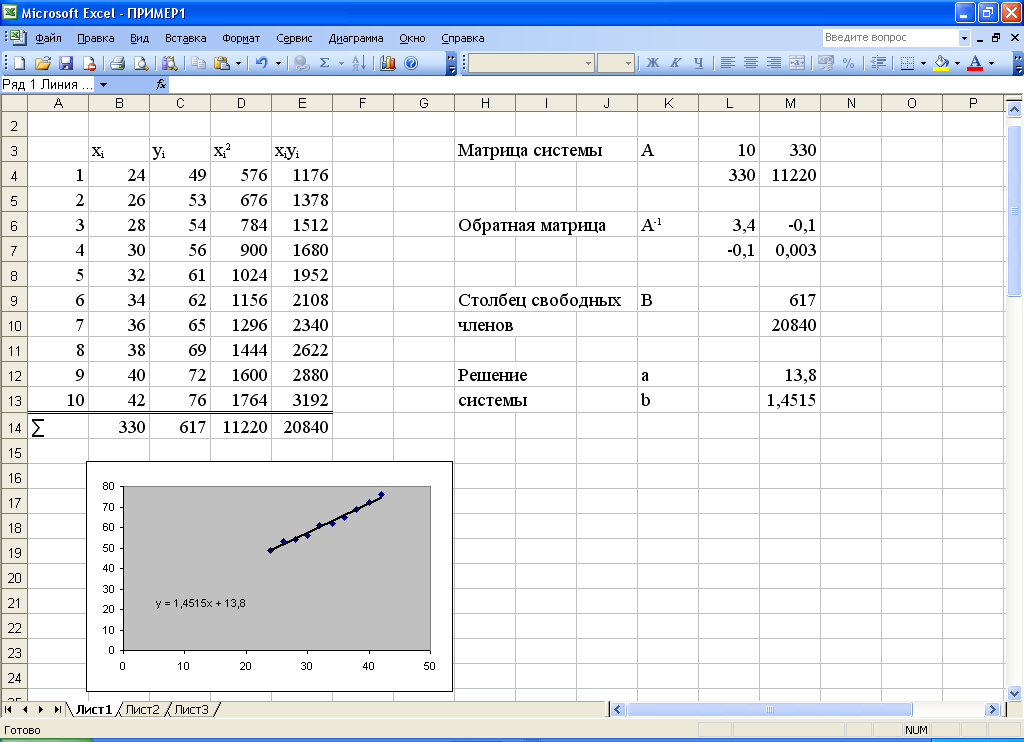

• В ячейках «L3:M4» запишем матрицу А.

• Найдем обратную матрицу 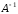. Для этого выделим область соответствующего размера диапазон «L6:M7» для записи обратной матрицы. Вызовем формулу массива

→ Математические → МОБР → ОК.

Зададим адреса матрицы А «L3:M4» и нажмемCtrl+Shift+Enterдля выполнения действия.

• В ячейках «M9:M10» запишем столбец свободных членовB.

• Умножим матрицу 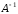на В и результат запишем в ячейках «M12:M13». Для этого выделим диапазон ячеек «M12:M13».

• Вызовем формулу массива

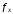→ Математические → МУМНОЖ → ОК. Зададим адреса перемножаемых матриц «L6:M7» и «M9:M10» и нажмем

Ctrl+Shift+Enterдля выполнения действия.

Таким образом, искомая эмпирическая функция имеет вид .

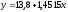4. Построим точечную диаграмму, используя Мастер диаграмм, который вызывается с помощью командыВставка → Диаграммаили при нажатии соответствующей кнопки на панели инструментов.

• Выделим данные, которые будут включены в диаграмму, т.е. ячейки «B4:C13».

• Выберем команду Вставка → Диаграмма (можно щелкнуть кнопкуМастер диаграмм на панели инструментов).

• На первом шаге работы Мастера диаграммвыберемТипдиаграммы вариантТочечная и щелкнемДалее.

• Можно пропустить остальные шаги и сразу нажать кнопку Готово. На экране появится встроенный график. При необходимости его можно перетащить в более удобное место, зацепив мышью за край области диаграммы.

• Добавим к исходной точечной диаграмме линию тренда. Для этого используем команду меню Диаграмма → Добавить линию тренда,которая появляется, если диаграмма выделена.

• В окне Линия трендаво вкладкеТипи выберем шаблон кривой. В нашем случаеЛинейная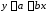. Во вкладкеПараметрыпоставим флажки:Показывать уравнение на диаграмме, поместить на диаграмму величину достоверности аппроксимацииR²и нажмем ОК. На диаграмме появится линия тренда и ее уравнение.