дифуравнения / дифуравнения-1 / тема5

Тема: Диференціальні рівняння вищих порядків. Рівняння, що допускають зниження порядку

Теоретичні відомості

Означення 1. Звичайним диференціальним рівнянням го порядку називається рівняння, яке пов’язує невідому функцію , незалежну змінну і похідні функції по до го порядку включно:

. (2.1)

Обмежимося розгляданням рівнянь го порядку, які можуть бути розрішеними відносно старшої похідної

. (2.2)

Означення 2. Функція називається загальним рішенням диференціального рівняння (2.1), якщо вона задовольняє рівнянню за будь – яких значень довільних констант .

Якщо невідома функція аргументу задана неявно рівністю , то така функція називається загальним інтегралом диференціального рівняння.

Означення 3. Частинним рішенням (частинним інтегралом) диференціального рівняння називається рішення , яке може бути отримане із загального при певних значеннях довільних констант .

Для знаходження частинного рішення диференціального рівняння необхідно знайти числові значення довільних констант . Для цього необхідно розв’язати задачу Коші.

Для рівняння (2.1) задача Коші ставиться таким чином: серед рішень рівняння треба знайти частинне рішення , яке задовольняє початковим умовам

Детальніше зупинимиося на диференціальному рівнянні другого порядку

. (2.3)

Функція є загальним рішенням рівняння (2.3) за умови, що вона задовольняє рівнянню при будь яких значеннях довільних констант .

Задача Коші для рівняння (2.3) полягає у знаходженні рішення , яке задовольняє початковим умовам

Розглянемо окремі види рівнянь вищих порядків.

1. Диференціальні рівняння виду

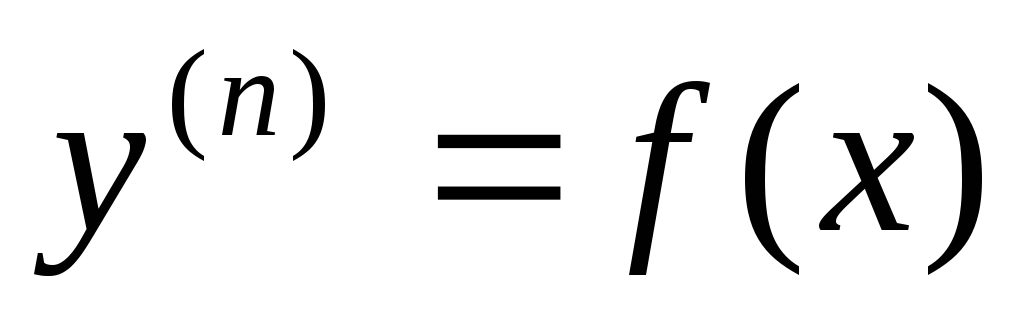
Простішим диференціальним рівнянням го порядку є рівняння, яке містить незалежну змінну (в окремому випадку постійну величину) і похідну го порядку:

, (2.4)

де диференційована в інтервалі функція.

Загальне рішення рівняння (2.4) знаходиться шляхом кратного інтегрування частин рівняння. Зокрема рішення рівняння другого порядку

(2.5)

знайдемо наступним способом: , тоді

. (2.6)

2. Рівняння другого порядку, які не містять невідомої функції

Рівняння виду

(2.7)

за допомогою підстановки , де нова невідома функція, зводиться до рівняння першого порядку , тобто в цьому випадку .

3. Рівняння другого порядку, які не містять незалежної змінної

Рівняння виду

(2.8)

за допомогою підстановки , де нова невідома функція, зводиться до рівняння першого порядку , тобто в цьому випадку .

Практичні завдання

Завдання 1. Розв’язати рівняння

1.1 .

1.2.

1.3. .

1.4. , якщо .

1.5. , якщо .

Завдання 2. Знайти загальний інтеграл диференціального рівняння:

2.1. .

2.2. .

2.3. .

2.4. .

2.5. .

2.6. .

Завдання 3. Розв’язати задачу Коші:

3.1. , якщо .

3.2. , якщо ..

3.3. , якщо .

3.4. , якщо .

3.5. , якщо .