дифуравнения / дифуравнения-1 / тема8

Тема: Лінійні неоднорідні рівняння другого порядку з постійними коефіцієнтами.

Метод варіації довільних постійних

Теоретичні відомості

Означення. Рівняння

, (1)

де неперервні функції, визначені в інтервалі , і називається лінійним неоднорідним диференціальним рівнянням го порядку.

Якщо права частина рівняння (1) має вигляд

, (2)

то мова йде про розв’язання лінійного неоднорідного рівняння зі спеціальною правою частиною.

В разі, якщо функція в правій частині рівняння (1) є довільною, тобто її не можна віднести до жодного з розглянутих вище випадків, для знаходження частинного рішення використовують метод варіації довільних постійних (метод Лагранжа). Він полягає в тому, що частинне рішення лінійного неоднорідного диференціального рівняння (1) шукатимемо в такому ж вигляді, як і загальне рішення відповідного лінійного однорідного диференціального рівняння шляхом заміни довільних постійних деякими неперервно диференційованими функціями змінної (варіації довільних змінних), тобто у вигляді

, (3)

де фундаментальна система рішень відповідного однорідного рівняння.

При цьому функції мають задовольняти лише співвідношенню, яке отримаємо в результаті підстановки функції (3) в рівняння (1).

Зокрема, для рівняння

, (4)

частинне рішення . Для того, щоб отримати найбільш просту систему для знаходження невідомих функцій , обчислимо , вважаючи суму доданків, які містять такою, що дорівнює нулю. Отже, і

, (5)

тоді

, (6)

. (7)

Підставимо (6) і (7) в (4):

або .

Оскільки фундаментальна система рішень відповідного однорідного рівняння, то і , а отже,

. (8)

Таким чином, похідні невідомих функцій можуть бути найденими з системи рівнянь (5) і (8):

(9)

Визначник системи (9) 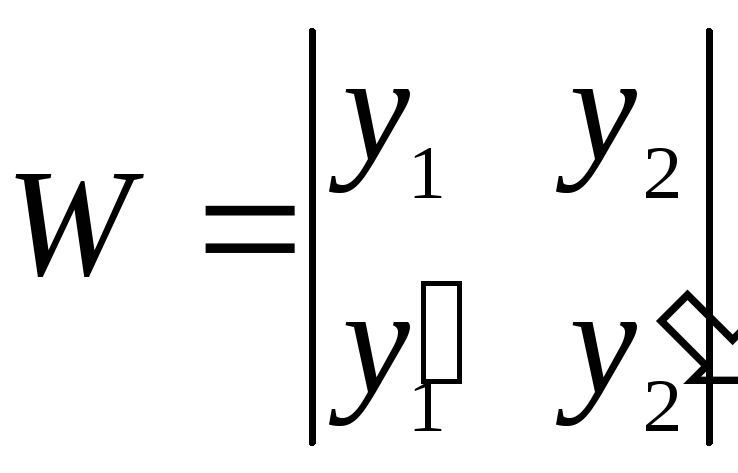є, очевидно визначником Вронського.

Тоді, за формулами Крамера,

, (10)

. (11)

Інтегруючи рівності (10) і (11), отримаємо

, (12)

, (13)

звідки, підставляючи знайдені функції в , знаходимо частинне рішення неоднорідного рівняння, після чого загальне рішення знайдемо у вигляді .

Практичні завдання

Завдання 1. Знайти загальне рішення рівняння методом варіації:

1.1. .

1.2. .

1.3. .

1.4.

1.5. .

1.6.

1.7. .

1.8. .

1.9. .

1.10. .

1.11.

1.12. .